« moi, en tout cas, je suis convaincu qu’Il ne jette pas les dés., »
~ Albert Einstein
- Variables aléatoires
- Variables aléatoires discrètes
- Variables aléatoires continues
- Variables aléatoires mixtes
- fonctions de Distribution cumulatives (CDF)
- fonction de densité de probabilité (PDF)
- exemple interactif CDF/PDF
variables aléatoires:

dites que vous deviez prendre une pièce de monnaie de votre poche et la jeter en l’air. Pendant qu’il traverse l’espace, que Pourriez-vous dire de son avenir?
atterrira-t-il la tête haute? Queues?, Plus que cela, combien de temps restera-t-il dans les airs? Combien de fois est-il rebondir? À quelle distance de l’endroit où il frappe le sol va-t-il enfin se reposer? D’ailleurs, va-t-il jamais toucher le sol? Jamais au repos?
pour certaines de ces questions, nous pouvons et nous contentons de réponses bien avant les observations; nous sommes à peu près sûrs que la gravité tiendra et que la pièce atterrira. Mais pour d’autres, nous n’avons pas d’autre choix que de porter un jugement et de parler en termes plus vagues, si nous voulons dire quelque chose d’utile sur l’avenir.,
en tant que scientifiques, il est, bien sûr, notre travail de dire quelque chose d’utile (ou à tout le moins, faisant autorité…), tandis que les pièces métaphoriques du système physique important sont encore dans l’air. Pile ou face peut même être une question de vie ou de mort. Nos pièces peuvent être, par exemple, divers débits de liquide de refroidissement possibles ou des masses d’uranium dans une centrale nucléaire. Nous nous soucions grandement de savoir quelles sont nos chances que nous obtenions des turbines vrombissantes au lieu d’une fusion.,
pour un déterministe strict, tous ces paris ont été réglés bien avant qu’une pièce, métaphorique ou non, ne soit jamais frappée; nous ne le savons tout simplement pas encore. Si nous connaissions seulement les forces appliquées au lancer d »une pièce, sa répartition exacte de la masse, les différents mouvements infimes de l » air dans la pièce… Si nous savions tout cela, alors nous saurions que le lancer de pièces particulier avait 100% de chances d’atterrir comme il atterrira, et zéro chance de tout autre résultat.
Mais, bien sûr, nous manquons souvent même d’une fraction mentionnable de cette connaissance du monde., En outre, il semble à des échelles extrêmement petites que les déterministes stricts ont absolument tort; il n’y a aucun moyen de prédire quand, par exemple, un atome d’uranium se divisera, et si un tel événement affecte le monde plus vaste, alors cet événement macro est vraiment imprévisible. Certains résultats sont vraiment dans l’air, instable jusqu’à ce qu’ils font partie du passé.
afin de faire face à cette réalité et de pouvoir décrire les états futurs d’un système de manière utile, nous utilisons des variables aléatoires., Une variable aléatoire est simplement une fonction qui relie chaque résultat physique possible d’un système à un nombre réel unique. En tant que tel, il existe trois sortes de variables aléatoires: discrètes, continues et mixtes. Dans les sections suivantes, ces catégories seront brièvement discutés et des exemples seront donnés.
Variables aléatoires discrètes:
considérez à nouveau notre lancer de pièces. Nous pourrions avoir des têtes ou des queues Comme résultats possibles. Si nous avons défini une variable, x, comme le nombre de têtes dans un seul lancer, alors x pourrait être 1 ou 0, rien d’autre., Une telle fonction, x, serait un exemple de variable aléatoire discrète. De telles variables aléatoires ne peuvent prendre que des valeurs discrètes. D’autres exemples sont les résultats d’un test de grossesse, ou le nombre d’élèves dans une salle de classe.
Variables aléatoires continues:
retour au lancer de pièces, et si nous voulions décrire la distance entre l’endroit où notre pièce s’est immobilisée et l’endroit où elle a touché le sol pour la première fois. Cette distance, x, serait une variable aléatoire continue car elle pourrait prendre un nombre infini de valeurs dans la plage continue des nombres réels., La pièce pourrait voyager 1 cm, ou de 1,1 cm, ou 1.11 cm, ou sur et sur. D’autres exemples de variables aléatoires continues seraient la masse des étoiles dans notre galaxie, le pH des eaux océaniques ou le temps de séjour d’un analyte dans un chromatographe en phase gazeuse.
Variables aléatoires mixtes:
Les variables aléatoires mixtes ont des composantes discrètes et continues. De telles variables aléatoires sont rarement rencontrées. Pour un exemple possible, cependant, vous pouvez mesurer le poids d »un échantillon et décider que tout poids mesuré en tant que valeur négative recevra une valeur de 0., De cette façon, la variable aléatoire a une composante discrète à x = 0 et une composante continue où x > 0.
fonctions de Distribution cumulatives (CDF):
la question, bien sûr, se pose de savoir comment décrire mathématiquement (et afficher visuellement) au mieux les variables aléatoires. Pour ces tâches, nous utilisons des fonctions de densité de probabilité (PDF) et des fonctions de densité cumulative (CDF). Comme les CDF sont plus simples à comprendre pour les variables aléatoires discrètes et continues que les PDF, nous allons d’abord expliquer les CDF.
envisagez de lancer un dé à 6 faces juste., Nous aurions 1 chance sur 6 d’obtenir l’une des valeurs possibles de la variable aléatoire(1, 2, 3, 4, 5, ou 6). Si nous traçons ces valeurs sur l’axe des x et l’intrigue de la probabilité de mesurer chaque valeur de x, ou toute valeur inférieure à x sur l’axe des y, nous aurons le CDF de la variable aléatoire.
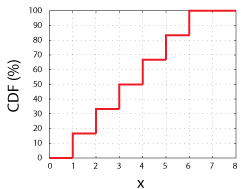
CDF pour une Juste 6-Sidded Dés. Notez que chaque pas est une hauteur de 16,67%, soit 1 sur 6.
Cette fonction, CDF(x), nous indique simplement les chances de mesurer n’importe quelle valeur jusqu’à et y compris X., En tant que tel, tous les CDF doivent tous avoir ces caractéristiques:
- Un CDF doit être égal à 0 lorsque x= -∞, et approcher 1 (ou 100%) lorsque x approche +∞. En termes simples, de tous les résultats possibles, il doit y avoir un résultat; la chance de lancer un dé à six faces et d’obtenir une valeur entre -∞ et ∞ est de 100%.
- La pente d’une CDF doit toujours être égale ou supérieure à zéro. Par exemple, considérez la possibilité de lancer un dé à 6 faces (juste ou non) et d’obtenir une valeur comprise entre 0 et 4., Que la chance ne peut pas être plus de chance d’obtenir une valeur comprise entre 0 et 5, parce que la cote des 1, 2, ou 3 à l’atterrissage face sont, bien sûr, toujours une fraction de chances d’obtenir 1, 2, 3, ou 4.
pour un exemple de variable aléatoire continue, l’applet suivant montre le CDF normalement distribué.,div>
| -5 | 5 |
| x | |
This important distribution is discussed elsewhere., Il suffit de noter que les caractéristiques d’un CDF décrites ci-dessus et expliquées pour une variable aléatoire discrète tiennent également pour des variables aléatoires continues.
pour des exemples plus intuitifs des propriétés des CDF, voir l’exemple interactif ci-dessous. En outre, les graphiques interactifs de nombreux autres CDF importants pour le domaine de la statistique et utilisés sur ce site peuvent être trouvés ici.
fonctions de densité de probabilité (PDF):
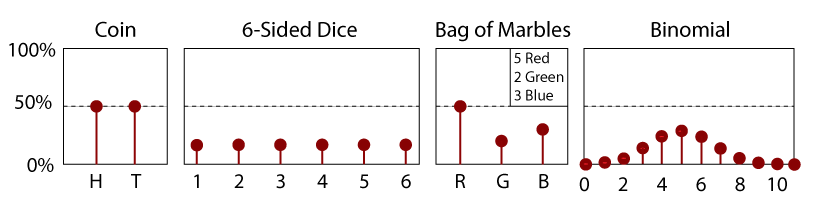
PDF pour un dé à 6 faces juste.
un PDF est simplement la dérivée d’un CDF., Ainsi, un PDF est également fonction d’une variable aléatoire, x, et sa magnitude sera une indication de la probabilité relative de mesurer une valeur particulière. Comme il s’agit de la pente D’un CDF, un PDF doit toujours être positif; il n’y a aucune cote négative pour aucun événement. De plus et par définition, l’aire sous la courbe D’un PDF(x) Entre -∞ et x est égale à son CDF (x). En tant que telle, l’aire entre deux valeurs x1 et x2 donne la probabilité de mesurer une valeur dans cette plage.
l’applet suivant montre un exemple de PDF pour une variable aléatoire normalement distribuée, X.,
Normal PDF
|
x:
| mean:
| stdev:
| f(x):
|
|
Notice, when the mean and standard deviations are equal, how the PDF correlates with the normal CDF in the section above., considérez également la différence entre un PDF continu et discret. Alors QU’un PDF discret (comme celui indiqué ci-dessus pour dice) vous donnera les chances d’obtenir un résultat particulier, les probabilités avec des PDF continus sont des questions de portée, pas de points discrets. Par exemple, il y a clairement 1 chance sur 6 (16,6%) de lancer un 3 sur un dé, comme on peut le voir dans son PDF. Mais quel est l’Impair de mesurer exactement zéro avec une variable aléatoire ayant un PDF normal et une moyenne de zéro, comme indiqué ci-dessus? Même si c’est la valeur où le PDF est le plus grand, la chance de mesurer exactement 0,00000..,. est, peut-être contre intuitivement, zéro. Les chances de mesurer un nombre aléatoire particulier avec une précision infinie sont, en fait, nulles. avec un PDF continu, vous pouvez plutôt demander quelles sont les chances que vous mesurerez entre deux valeurs pour obtenir une probabilité supérieure à zéro. Pour trouver cette probabilité, nous utilisons simplement le CDF de notre variable aléatoire., Parce que le CDF nous indique l’Impair de mesurer une valeur ou tout ce qui est inférieur à cette valeur, pour trouver la probabilité de mesurer entre deux valeurs, x1 et x2 (où x1 > x2), nous devons simplement prendre la valeur du CDF à x1 et en soustraire la valeur Par exemple, en utilisant le CDF normal dans l’applet ci-dessus (Avec μ=0 et σ=1), si nous voulions connaître les chances de mesure entre 0,01 et 0,02, nous trouvons CDF(x=0,1)=53,9828% et CDF(x=0,2)=57,9260%. Ensuite, la différence, CDF(0.2) – CDF(0.1), nous donne les chances d’environ 3.9% de mesurer un x entre 0.1 et 0.2., pour des exemples visuels plus intuitifs des propriétés des PDF, voir l’exemple interactif ci-dessous. En outre, des tracés interactifs de nombreux PDF importants utilisés sur ce site peuvent être vus ici. |
|||||||||||||||||