Statistiky Definice > ANOVA
Obsah:
- ANOVA Test
- Jeden Způsob, ANOVA
- Two Way ANOVA
- Co je MANOVA?
- co je faktoriální ANOVA?
- Jak spustit ANOVA
- ANOVA vs. T-Test
- Opakovaná měření ANOVA
- kulovitého tvaru
ANOVA Test
Co je ANOVA?, Podívejte se na video pro úvod, nebo si přečtěte níže:
stále máte potíže? Chegg.com spojí vás s učitelem (vaše první lekce je zdarma!).
ANOVA test je způsob, jak zjistit, zda jsou výsledky průzkumu nebo experimentu významné. Jinými slovy, pomáhají vám zjistit, zda potřebujete odmítnout nulovou hypotézu nebo přijmout alternativní hypotézu.
v podstatě testujete skupiny, abyste zjistili, zda je mezi nimi rozdíl., Příklady, kdy možná budete chtít vyzkoušet různé skupiny:
- skupina psychiatrických pacientů jsou to tři různé terapie: poradenství, léky a biofeedback. Chcete zjistit, zda je jedna terapie lepší než ostatní.
- výrobce má dva různé procesy pro výrobu žárovek. Chtějí vědět, zda je jeden proces lepší než druhý.
- studenti z různých vysokých škol absolvují stejnou zkoušku. Chcete zjistit,jestli jedna vysoká škola překonává druhou.
co znamená „jednosměrná“ nebo „obousměrná cesta“?,
jednosměrný nebo obousměrný označuje počet nezávislých proměnných (IVs)v analýze testu rozptylu.
- jednosměrná má jednu nezávislou proměnnou (se 2 úrovněmi). Například: značka obilovin,
- obousměrná má dvě nezávislé proměnné (může mít více úrovní). Například: značka obilovin, kalorií.
co jsou “ skupiny „nebo“úrovně“?
skupiny nebo úrovně jsou různé skupiny ve stejné nezávislé proměnné. Ve výše uvedeném příkladu mohou být vaše úrovně pro „značku obilovin“ Lucky Charms, rozinky otruby, kukuřičné lupínky — celkem tři úrovně., Vaše úrovně pro „kalorií“ může být: slazené, neslazené — celkem dvě úrovně.
řekněme, že studujete, zda je alkoholická podpůrná skupina a individuální poradenství kombinované nejúčinnější léčbou pro snížení konzumace alkoholu. Můžete rozdělit účastníky studie do tří skupin nebo úrovní:
- pouze léky,
- léky a poradenství,
- pouze poradenství.
vaše závislá proměnná by byla počet konzumovaných alkoholických nápojů denně.,
Pokud vaše skupiny nebo úrovně mají hierarchickou strukturu (každá úroveň má jedinečné podskupiny), použijte pro analýzu vnořenou ANOVU.
co znamená“ replikace“?
je to, zda replikujete (tj. duplikujete) svůj test s více skupinami. S two way ANOVA s opakováním , máte dvě skupiny a jednotlivci v rámci této skupiny jsou dělat více než jednu věc (tj. dvě skupiny studentů ze dvou škol, přičemž dva testy). Pokud máte pouze jednu skupinu, která provádí dva testy, použili byste bez replikace.
typy testů.,
existují dva hlavní typy: jednosměrný a obousměrný. Obousměrné testy mohou být s replikací nebo bez ní.
- jednosměrná ANOVA mezi skupinami: používá se, když chcete otestovat dvě skupiny, abyste zjistili, zda je mezi nimi rozdíl.
- obousměrná ANOVA bez replikace: používá se, když máte jednu skupinu a dvakrát testujete stejnou skupinu. Například testujete jednu sadu jedinců před a po užití léku, abyste zjistili, zda to funguje nebo ne.
- obousměrná ANOVA s replikací: dvě skupiny a členové těchto skupin dělají více než jednu věc., Například dvě skupiny pacientů z různých nemocnic zkoušejí dvě různé terapie.
zpět na začátek
jednosměrná ANOVA
jednosměrná ANOVA se používá k porovnání dvou prostředků ze dvou nezávislých (nesouvisejících) skupin pomocí F-distribuce. Nulová hypotéza testu je, že oba prostředky jsou stejné. Významný výsledek tedy znamená, že oba prostředky jsou nerovné.
Příklady, kdy použít jeden způsob, ANOVA
Situace 1: máte skupinu osob, které náhodně rozdělili do menších skupin a plněním různých úkolů., Můžete například studovat účinky čaje na hubnutí a tvořit tři skupiny: zelený čaj, černý čaj a žádný čaj.
situace 2: podobná situaci 1, ale v tomto případě jsou jednotlivci rozděleni do skupin na základě atributu, který mají. Například byste mohli studovat sílu nohou lidí podle hmotnosti. Můžete rozdělit účastníky do hmotnostních kategorií (obézní, nadváha a normální) a měřit jejich sílu nohou na hmotnostním stroji.,
omezení jednosměrného ANOVA
jednosměrná ANOVA vám řekne, že alespoň dvě skupiny se od sebe lišily. Ale neřekne vám, Které skupiny byly jiné. Pokud váš test se vrací významný f-statistika, možná budete muset spustit ad hoc test (jako Nejméně Významný Rozdíl test), aby vám přesně říct, které skupiny byl rozdíl v prostředcích.
Zpět na začátek
obousměrná Anova
obousměrná ANOVA je rozšíření jednosměrné ANOVA. Jedním způsobem máte jednu nezávislou proměnnou ovlivňující závislou proměnnou., S obousměrnou anovou existují dva nezávislí. Použijte obousměrnou ANOVU, pokud máte jednu proměnnou měření (tj. kvantitativní proměnnou) a dvě nominální proměnné. Jinými slovy, pokud má váš experiment kvantitativní výsledek a máte dvě kategorické vysvětlující proměnné, je vhodná obousměrná ANOVA.
například, možná budete chtít zjistit, zda existuje interakce mezi příjmem a pohlavím pro úroveň úzkosti při pracovních pohovorech. Úroveň úzkosti je výsledek nebo proměnná, kterou lze měřit. Pohlaví a příjem jsou dvě kategorické proměnné., Tyto kategorické proměnné jsou také nezávislé proměnné, které se nazývají faktory dvojím způsobem ANOVA.
faktory lze rozdělit na úrovně. Ve výše uvedeném příkladu by úroveň příjmů mohla být rozdělena do tří úrovní: nízký, střední a vysoký příjem. Pohlaví lze rozdělit do tří úrovní: muž, žena, a transgender. Léčebné skupiny jsou všechny možné kombinace faktorů. V tomto příkladu by byly 3 x 3 = 9 léčebných skupin.
hlavní efekt a interakční efekt
výsledky z obousměrného ANOVA vypočítají hlavní efekt a interakční efekt., Hlavní efekt je podobný jedné cestě ANOVA: účinek každého faktoru je zvažován samostatně. S interakčním účinkem jsou všechny faktory zvažovány současně. Účinky interakce mezi faktory se snáze testují, pokud je v každé buňce více než jedno pozorování. Pro výše uvedený příklad lze do buněk zadat více stresových skóre. Pokud do buněk zadáte více pozorování, musí být číslo v každé buňce stejné.
dvě nulové hypotézy jsou testovány, pokud umístíte jedno pozorování do každé buňky., Pro tento příklad by tyto hypotézy byly:
H01: všechny příjmové skupiny mají stejný střední stres.
H02: všechny genderové skupiny mají stejný střední stres.
pro více pozorování v buňkách byste také testovali třetí hypotézu:
H03: faktory jsou nezávislé nebo interakční efekt neexistuje.
pro každou testovanou hypotézu se vypočítá F-statistika.
předpoklady pro obousměrnou ANOVU
- populace musí být blízká normálnímu rozdělení.
- vzorky musí být nezávislé.
- populační odchylky musí být stejné.,
- skupiny musí mít stejné velikosti vzorku.
zpět na začátek
co je MANOVA?
MANOVA je jen ANOVA s několika závislými proměnnými. Je to podobné mnoha jiným testům a experimentům v tom, že je účelem zjistit, zda je proměnná odezvy (tj. vaše závislá proměnná) změněna manipulací s nezávislou proměnnou. Test pomáhá odpovědět na mnoho výzkumných otázek, včetně:
- mají změny nezávislých proměnných statisticky významné účinky na závislé proměnné?
- jaké jsou interakce mezi závislými proměnnými?,
- jaké jsou interakce mezi nezávislými proměnnými?
Manova Example
Předpokládejme, že jste chtěli zjistit, zda rozdíl v učebnicích ovlivnil skóre studentů v matematice a vědě. Zlepšení v matematice a vědě znamená, že existují dvě závislé proměnné, takže MANOVA je vhodná.
ANOVA vám dá jednu (univariátní) hodnotu f, zatímco MANOVA vám dá multivariační hodnotu F. MANOVA testuje více závislých proměnných vytvořením nových, umělých, závislých proměnných, které maximalizují skupinové rozdíly., Tyto nové závislé proměnné jsou lineární kombinace měřených závislých proměnných.
Interpretaci MANOVA výsledky
Pokud vícerozměrné F hodnota znamená, že test je statisticky významný, to znamená, že něco je významné. Ve výše uvedeném příkladu byste nevěděli, zda se skóre matematiky zlepšilo, skóre vědy se zlepšilo (nebo obojí)., Jakmile budete mít významný výsledek, pak budete muset podívat na jednotlivé součásti (jednorozměrné testy F), kde závislá proměnná(y) přispěl k statisticky významný výsledek.
Výhody a Nevýhody MANOVA vs. ANOVA
Výhody
- MANOVA umožňuje testovat více závislé proměnné.
- MANOVA může chránit před chybami typu I.
nevýhody
- MANOVA je mnohonásobně komplikovanější než ANOVA, což z něj činí výzvu zjistit, které nezávislé proměnné ovlivňují závislé proměnné.,
- jeden stupeň svobody je ztracen přidáním každé nové proměnné.
- závislé proměnné by měly být co nejvíce nekorelovány. Pokud jsou korelovány, ztráta ve stupních volnosti znamená, že není mnoho výhod v zahrnutí více než jedné závislé proměnné do testu.
Reference:
(SFSU)
zpět na začátek
co je faktoriální ANOVA?
faktoriální ANOVA je analýza testu rozptylu s více než jednou nezávislou proměnnou nebo „faktorem“. Může také odkazovat na více než jednu úroveň nezávislé proměnné., Například experiment s léčivou skupinou a kontrolní skupinou má jeden faktor (léčba), ale dvě úrovně (léčba a kontrola). Termíny „obousměrný“ a „třícestný“ se vztahují k počtu faktorů nebo počtu úrovní ve vašem testu. Čtyřcestná ANOVA a vyšší jsou zřídka používána, protože výsledky testu jsou složité a obtížně interpretovatelné.
- obousměrná ANOVA má dva faktory (nezávislé proměnné) a jednu závislou proměnnou. Například čas strávený studiem a předchozí znalosti jsou faktory, které ovlivňují, jak dobře děláte na testu.,
- třícestná ANOVA má tři faktory (nezávislé proměnné) a jednu závislou proměnnou. Například, čas strávený studiem, předchozí znalosti, a hodin spánku jsou faktory, které ovlivňují, jak dobře děláte na test
Factorial ANOVA je efektivní způsob provedení testu. Namísto provádění řady experimentů, kde testujete jednu nezávislou proměnnou proti jedné závislé proměnné, můžete testovat všechny nezávislé proměnné současně.
variabilita
v jednosměrné Anově je variabilita způsobena rozdíly mezi skupinami a rozdíly ve skupinách., Ve faktoriální Anově jsou každá úroveň a faktor vzájemně spárovány („zkřížené“). To vám pomůže zjistit, jaké interakce se děje mezi úrovněmi a faktory. Pokud existuje interakce, pak rozdíly v jednom faktoru závisí na rozdílech v jiném.
Řekněme, že jste vedli obousměrnou ANOVU, abyste otestovali mužský / ženský výkon na závěrečné zkoušce. Subjekty měly buď 4, 6 nebo 8 hodin spánku.,
- IV1: POHLAVÍ (Muž/Žena)
- IV2: SPÁNEK (4/6/8)
- DV: Závěrečná Zkouška Skóre
obousměrný factorial ANOVA by vám pomohou odpovědět na následující otázky:
- Je sex hlavní účinek? Jinými slovy, liší se muži a ženy výrazně ve výkonu zkoušky?
- je spánek hlavním účinkem? Jinými slovy, liší se lidé, kteří měli 4,6 nebo 8 hodin spánku, výrazně ve svém výkonu?
- existuje významná interakce mezi faktory? Jinými slovy, jak hodiny spánku a sexu interagují s ohledem na výkon zkoušky?,
- lze v různých úrovních spánku nalézt jakékoli rozdíly v pohlaví a výkonu zkoušky?
předpoklady faktoriální ANOVY
- normálnost: závislá proměnná je normálně distribuována.
- nezávislost: pozorování a skupiny jsou na sobě nezávislé.
- rovnost rozptylu: populační odchylky jsou stejné napříč faktory / úrovněmi.
jak spustit ANOVA
tyto testy jsou velmi časově náročné ručně. Téměř v každém případě budete chtít používat software., Například v Excelu je k dispozici několik možností:
- obousměrná ANOVA v Excelu s replikací a bez replikace.
- jednosměrná ANOVA v aplikaci Excel 2013.
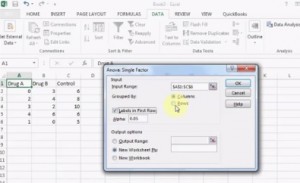
spuštění testu v Excelu.
ANOVA testy ve statistických balíčcích jsou spuštěny na parametrických datech. Pokud máte hodnost nebo objednat údajů, budete chtít spustit neparametrický ANOVA (obvykle našel pod jiným nadpisem v softwaru, jako „neparametrické testy“).,
Takto
je nepravděpodobné, že budete chtít udělat tento test ručně, ale pokud musíte, to jsou kroky, které budete chtít vzít:
- Najít pro každou ze skupin.
- Najděte celkový průměr (průměr kombinovaných skupin).
- Najděte variaci uvnitř skupiny; celková odchylka skóre každého člena od průměru skupiny.
- Najděte rozdíly mezi skupinami: odchylka každé skupiny znamená celkový průměr.
- Najděte statistiku F: poměr mezi variací skupiny a variací ve skupině.
ANOVA vs., T Test
t-test studenta vám řekne, zda existuje významná změna mezi skupinami. T-test porovnává prostředky, zatímco ANOVA porovnává rozdíly mezi populacemi.
můžete technicky provést řadu t-testů na vašich datech. Nicméně, jak skupiny růst v počtu, můžete skončit s mnoha párových srovnání, které musíte spustit. ANOVA vám dá jediné číslo (f-statistika) a jednu P-hodnotu, která vám pomůže podpořit nebo odmítnout nulovou hypotézu.,
Zpět na začátek
opakovaná opatření ANOVA
opakovaná opatření ANOVA je téměř stejná jako jednosměrná ANOVA, s jedním hlavním rozdílem: testujete související skupiny, nikoli nezávislé. Říká se tomu opakovaná opatření, protože stejná skupina účastníků se měří znovu a znovu. Například byste mohli studovat hladinu cholesterolu ve stejné skupině pacientů po 1, 3 a 6 měsících po změně stravy. Pro tento příklad je nezávislá proměnná “ čas „a závislá proměnná je“ cholesterol.,“Nezávislá proměnná se obvykle nazývá faktor uvnitř subjektů.
opakovaná opatření ANOVA je podobná jednoduchému vícerozměrnému designu. V obou testech jsou stejní účastníci měřeni znovu a znovu. Při opakovaných opatřeních se však stejná charakteristika měří s jiným stavem. Například krevní tlak se měří nad stavem „čas“. Pro jednoduchý vícerozměrný design je to charakteristika, která se mění. Například byste mohli měřit krevní tlak, srdeční frekvenci a rychlost dýchání v průběhu času.,
Důvody pro použití Opakovaná měření ANOVA
- Když budete sbírat data od stejných účastníků v průběhu času, individuální rozdíly (zdroj mezi skupinami rozdíly) jsou sníženy nebo odstraněny.
- testování je silnější, protože velikost vzorku není rozdělena mezi skupiny.
- test může být ekonomický, protože používáte stejné účastníky.,
Předpoklady pro Opakovaná měření ANOVA
výsledky z vašeho opakovaná měření ANOVA, bude platná, pouze pokud tyto předpoklady nebyly porušeny:
- musí být jedna z nezávisle proměnných a jednou závisle proměnné.
- závislá proměnná musí být spojitá proměnná, na intervalové stupnici nebo stupnici poměru.
- nezávislá proměnná musí být kategorická, buď na jmenovité stupnici nebo pořadové stupnici.
- v ideálním případě jsou úrovně závislosti mezi páry skupin stejné („sphericity“)., Opravy jsou možné, pokud je tento předpoklad porušen.
opakovaná opatření ANOVA v SPSS: kroky
Krok 1: Klikněte na “ analyzovat „a poté najeďte myší na“ obecný lineární Model.“Klikněte“ Opakovaná Opatření.“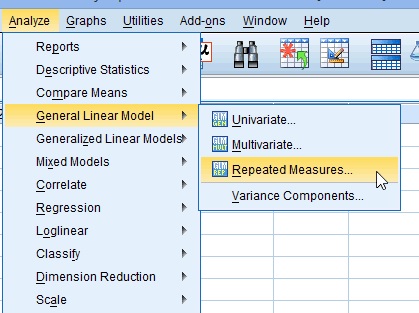
Krok 2: nahraďte název“ factor1 “ něčím, co představuje vaši nezávislou proměnnou. Například byste mohli dát “ věk „nebo“ čas.“
Krok 3: Zadejte “ počet úrovní.“Kolikrát byla měřena závislá proměnná. Pokud byste například měřili každý týden celkem 4 týdny, toto číslo by bylo 4.,
Krok 4: Klikněte na tlačítko „Přidat“ a poté pojmenujte závislou proměnnou.
Krok 5: Klikněte na tlačítko“ Přidat“. Objeví se okno definující opakovaná opatření. Klikněte na tlačítko“ Definovat“.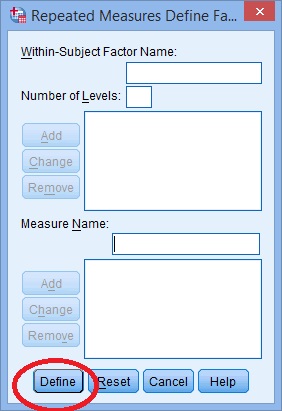
Krok 6: Pomocí kláves se šipkami pohybovat vaše proměnné z levé do pravé tak, že vaše obrazovka vypadá podobně jako na obrázku níže: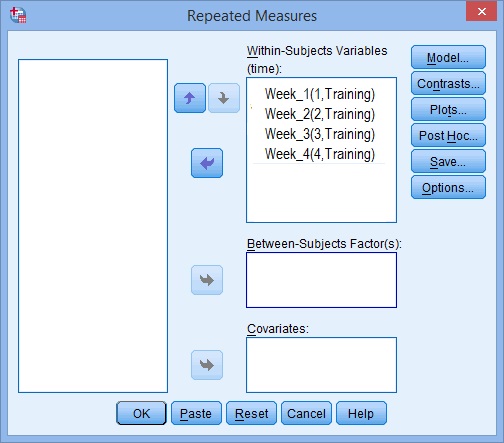
Krok 7: Klikněte na „Pozemky“ a pomocí kláves se šipkami transfer faktor z levého pole na Vodorovné Ose okno.
Krok 8: Klikněte na „Přidat“ a poté na tlačítko „Pokračovat“ v dolní části okna.,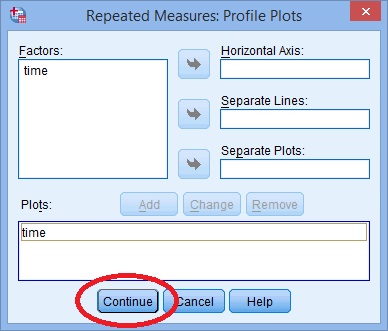
Krok 9: klikněte na „možnosti“ a poté přeneste své faktory z levého pole na zobrazovací prostředky pro pole vpravo.
Krok 10: Klikněte na následující zaškrtávací políčka:
- Porovnejte hlavní efekty.
- Popisná statistika.
- odhady velikosti efektu.
krok 11: V rozbalovací nabídce pod nastavením intervalu spolehlivosti vyberte „Bonferroni“.
krok 12: Klikněte na “ Pokračovat „a poté klikněte na“ OK “ pro spuštění testu.,
Zpět na začátek
kulovitého tvaru
Ve statistice, kulovitého tvaru (ε) odkazuje na Mauchly kulovitého tvaru test, který byl vyvinut v roce 1940 John W. Mauchly, který společně vyvinuli první univerzální elektronický počítač.
definice
Sphericity se používá jako předpoklad v opakovaných opatřeních ANOVA. Předpoklad uvádí, že rozdíly rozdílů mezi všemi možnými skupinovými páry jsou stejné. Pokud vaše data poruší tento předpoklad, může to vést ke zvýšení chyby typu I (nesprávné odmítnutí nulové hypotézy).,
u opakovaných opatření je velmi běžné, že ANOVA vede k porušení předpokladu. Pokud byl předpoklad porušen, byly vyvinuty opravy, které mohou zabránit zvýšení chybovosti typu I. Korekce se aplikuje na stupně volnosti v F-distribuci.
Mauchly kulovitého tvaru Zkoušky
Mauchly test pro kulovitého tvaru lze spustit ve většině statistických software, kde to má tendenci být standardní test pro kulovitého tvaru. Mauchlyho test je ideální pro vzorky střední velikosti., V malých vzorcích může selhat detekce sféričnosti a ve velkých vzorcích může být příliš detekována.
pokud test vrátí malou hodnotu p (p ≤.05), to je známka toho, že vaše údaje porušily předpoklad. Následující obrázek výstupu SPSS pro ANOVU ukazuje, že význam“ sig “ připojený k Mauchly je .274. To znamená, že předpoklad nebyl pro tento soubor údajů porušen.
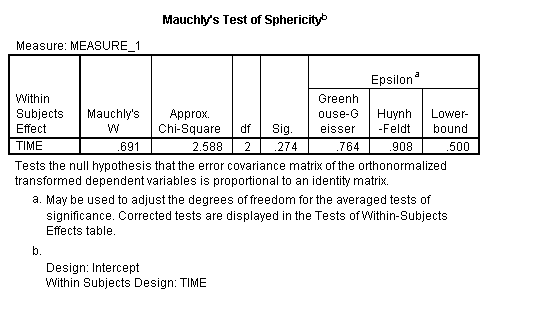
Obrázek: UVM.,EDU
Ty by zpráva výše uvedený výsledek jako „Mauchly Testu je uvedeno, že předpokladu kulovitého tvaru nebyla porušena, χ2(2) = 2.588, p = .274.“
Pokud váš test vrátil malou hodnotu p, měli byste použít opravu, obvykle buď:
- greehouse-Geisser correction.
- Huynh-Feldt korekce.
když ε ≤ 0.75 (nebo nevíte, jaká je hodnota pro statistiku), použijte korekci Greenhouse-Geisser.
když ε > .75, použij Huynh-Feldtovu korekci.,
Zpět na začátek
Velký
ANOVA vs Regrese
——————————————————————————
Potřebujete pomoci s úkoly nebo zkoušky otázka? S Chegg studie, můžete získat krok za krokem řešení vašich otázek od odborníka v oboru. Vaše první 30 minut s Chegg tutor je zdarma!