Cox Proporcionálních Rizik, Model

jsem dříve psal o tom, jak vypočítat Kaplan–Meierovy křivky pro přežití data. Jako neparametrický odhad odvádí dobrou práci při rychlém pohledu na křivku přežití datového souboru. To, co vám však nedovolí, je modelovat dopad kovariátů na přežití. V tomto článku se zaměříme na model Cox proporcional Hazards, jeden z nejpoužívanějších modelů pro data o přežití.

půjdeme do nějaké hloubky, jak vypočítat odhady., To je cenné, protože uvidíme, že odhady závisí pouze na uspořádání selhání a nikoli na jejich skutečných časech. Také se budeme stručně diskutovat některé složité otázky o kauzální inference, které jsou zvláštní pro analýzu přežití.

obvykle přemýšlíme o údajích o přežití, pokud jde o křivky přežití, jako je ta níže.,

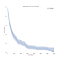
Na ose x máme čas ve dnech. Na ose y máme (odhad) procento (technicky, podíl) subjektů v populaci, které do té doby „přežívají“. Přežít může být obrazové nebo doslovné., To by mohlo být, zda lidé žijí do určitého věku, zda stroj dělá to určitou dobu, aniž se poškodí, nebo by to mohlo být, zda někdo zůstává nezaměstnaných určitou dobu poté, co ztratil svou práci.

zásadní komplikací v analýze přežití je to, že některé subjekty nemají pozorovanou „smrt“. Mohou být stále naživu, stroj může stále fungovat, nebo někdo může být v době shromažďování údajů stále nezaměstnaný., Taková pozorování se nazývají „správně cenzurovaná“ a řešení cenzury znamená, že analýza přežití vyžaduje různé statistické nástroje.

označujeme funkci survivor jako S, funkci času. Jeho výstupem je procento subjektů přežívajících v čase t. (opět je to technicky poměr mezi 0 a 1, ale obě slova použiji zaměnitelně). Pro jednoduchost uděláme technický předpoklad, že pokud budeme čekat dostatečně dlouho, všechny subjekty „zemřou.“

budeme indexovat subjekty s indexem jako i nebo j., Selhání krát celé populace bude uvedeno s podobným indexem na časové proměnné „t“.

Další jemnost je zvážit, zda jsou na léčení čas jako diskrétní (týden po týdnu), nebo kontinuální. Filozoficky řečeno, čas měříme pouze v diskrétních krocích (do nejbližší sekundy, řekněme)., Naše data nám obvykle sdělí, pouze pokud někdo zemřel v daném roce nebo pokud stroj v daný den selhal. Budu tam a zpět mezi diskrétními a spojitými případy v zájmu zachování expozice co nejjasnější.

Když se snažíme modelovat účinky proměnnými (např. věk, pohlaví, rasu, výrobce stroje) bude obvykle mít zájem na pochopení vlivu těchto proměnných na Riziko Hodnotit. Míra nebezpečnosti je okamžitá pravděpodobnost přechodu selhání/smrti/stavu v daném čase t, podmíněná tím, že již přežila tak dlouho., Označíme to λ (t). Léčení čas jako diskrétní:

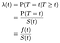
Kde f je celková hustota pravděpodobnosti selhání v čase t. Můžeme sjednotit diskrétní a kontinuální případech tím, že delta funkce hustoty pravděpodobnosti „funkce“. Výsledek λ = f / S je tedy stejný pro kontinuální případ.

pojďme opravit příklad., Podívejme se na kontext klinické studie, kdy lék zpočátku způsobuje, že onemocnění přechází do remise. Řekneme, že droga „selže“ pro subjekt, když nemoc začne postupovat pro subjekt. Nakonec předpokládejme, že stavy onemocnění subjektů se měří každý týden. Pak, pokud λ(3) = 0,1, to znamená, že existuje 10% šance, že pro daný předmět, pokud jsou stále v remisi než týden 3, jejich nemoc začne k pokroku ve 3.týdnu. Dalších 90% zůstane v remisi.,

dále je celková funkce hustoty pravděpodobnosti f pouze derivací S vzhledem k času. (Opět platí, že pokud je čas diskrétní, f je jen součet některých funkcí delta).,341fa8b2″>

To znamená, že pokud víme, že výstražná funkce, můžeme to vyřešit diferenciální rovnici pro Y:

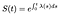
Pokud je čas diskrétní, integrál jako součet delta funkce, jen se změní na součet nebezpečí na každém diskrétním časem.,

dobře, to shrnuje notaci a základní pojmy, které budeme potřebovat. Pojďme k diskusi o modelech.

Non-, Polo-a Plně Parametrické Modely

Jak jsem již řekl dříve, jsme se obvykle zajímají o modelování míry rizika λ.

v neparametrickém modelu neděláme žádné předpoklady o funkční formě λ. Křivka Kaplan-Meier je v tomto případě odhadem maximální pravděpodobnosti. Nevýhodou je, že to ztěžuje modelování jakýchkoli účinků kovariátů. Je to trochu jako použití rozptylového spiknutí k pochopení účinku kovariátu., Ne nutně tak užitečné jako plně parametrický model, jako je lineární regrese.

v plně parametrickém modelu předpokládáme přesnou funkční formu λ. Diskuse o plně parametrických modelech je sama o sobě úplným článkem, ale stojí za to velmi krátkou diskusi. Níže uvedená tabulka ukazuje tři nejběžnější plně parametrické modely. Každý je zobecněn dalším, který se pohybuje od 1 do 2 do 3 parametrů. Funkční forma funkce nebezpečí je zobrazena ve středním sloupci. Logaritmus funkce nebezpečí je také zobrazen v posledním sloupci., Všechny parametry (ɣ, α, μ) jsou považovány za pozitivní, s výjimkou toho, že μ může být 0 ve zobecněné Weibullově distribuci (reprodukce weibullovy distribuce).

Při pohledu na logaritmus nám ukazuje, že exponenciální model předpokládá, že nebezpečí, funkce je konstantní. Weibullova modelu předpokládá, že se zvyšuje, pokud α>1, konstantní, pokud α=1, a snižuje, pokud α<1., Zobecněný Model Weibull začíná stejným způsobem jako model Weibull (na začátku ln S = 0). Poté se začne platit další termín.

problém s těmito modely je, že mají silné předpoklady o datech. V určitých kontextech mohou existovat důvody domnívat se, že tyto modely jsou dobré. Ale s těmito a několika dalšími dostupnými možnostmi existuje silné riziko vyvození nesprávných závěrů v důsledku nesprávné specifikace modelu.

proto je Cox proporcionální nebezpečí, poloparametrický model tak populární., Žádné funkční předpokladů o tvaru Nebezpečnosti Funkce; místo toho, funkční-formě domněnky o vlivu dalších proměnných sám.,

Cox Proporcionálních Rizik, Model

Cox Proporcionálních Rizik, Model je obvykle podáván v čase t, kovariance vektoru x, a koeficient vektoru β jako

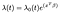
kde λₒ je libovolná funkce času, základní nebezpečí. Tečka součin X a β se bere v exponentu stejně jako ve standardní lineární regresi., Bez ohledu na hodnoty kovariátů sdílejí všechny subjekty stejnou základní nebezpečnost λ λ. Poté se úpravy provádějí na základě kovariátů.

Interpretace Výsledků

Předpokládejme na chvíli, že máme se vešly Cox Proporcionálních Rizik modelu pro naše data, která se skládala z

1. sloupce určující čas pro každý předmět
2. sloupce uvede, zda předmět byl „pozorován“ (selhal, nebo, v našem preferovaný příklad, aby se jejich onemocnění pokroku). Hodnota 1 znamená, že subjekt měl pokrok v nemoci., Hodnota 0 znamená, že v poslední době pozorování nemoc nepokročila. Pozorování bylo cenzurováno.
3. sloupce pro naše kovariáty x.

po fit získáme hodnoty pro β. Například předpokládejme, že pro jednoduchost existuje jediný kovariát. Hodnota β=0,1 znamená, že zvýšení veličinou o částku 1 vede k přibližně 10% vysoká pravděpodobnost progrese onemocnění v daném okamžiku., Přesná hodnota je ve skutečnosti

Pro malé hodnoty β, hodnota β sám o sobě je docela dobrá aproximace přesné zvýšení nebezpečí. Pro větší hodnoty β musí být vypočítáno přesné množství.

dalším způsobem, jak vyjádřit β = 0, 1, je to, že s nárůstem X se riziko zvyšuje rychlostí 10% na zvýšení x o 1. Větší 10.,52% vzniká z (nepřetržitého) míchání, stejně jako se složeným úrokem.

také β=0 znamená žádný účinek a β negativní znamená, že s tím, jak se kovariát zvyšuje, existuje menší riziko. Všimněte si, že na rozdíl od standardních regresí neexistuje žádný intercept termín. Místo toho je záchyt absorbován do výchozího nebezpečí λ λ, které lze také odhadnout (viz níže).

nakonec za předpokladu, že jsme odhadli základní funkci nebezpečnosti,můžeme vytvořit funkci přeživšího.,

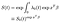
základní funkcí je umocněné exp(xʹß) faktor pocházející z proměnné. Je třeba věnovat určitou pozornost interpretaci základní přeživší funkce, která zhruba hraje roli intercept termínu v pravidelné lineární regresi. Pokud byly kovariáty soustředěny (průměr 0), pak představuje funkci přeživšího pro „průměrný“ subjekt.,

Odhad Cox Proporcionálních Rizik, Model

V roce 1970, David Cox, Britský matematik, navrhl způsob, jak odhadnout β, aniž byste museli odhadnout základní riziko λₒ. Opět lze odhadnout základní riziko. Jak již bylo zmíněno dříve, uvidíme, že je to uspořádání pozorovaných selhání, na kterých záleží, ne samotné časy.

před skokem do odhadu stojí za to diskutovat o vazbách. Od doby, co jsme se obvykle pouze sleduje data v diskrétních krocích, je možné, že dva neúspěchy by mohlo dojít ve stejnou dobu., Například dva stroje mohou selhat ve stejném týdnu a záznam se provádí pouze jednou týdně. Tyto vazby dělají analýzu situace poměrně komplikovanou, aniž by přidaly mnoho vhledu. V důsledku toho budu odvodit odhady v případě, že žádné vazby.

připomeňme, že naše data se skládají z pozorování některých poruch čísel v diskrétním čase. Nechť R (t) označuje populaci „ohroženou“ v době t. pokud subjekt v naší studii selhal (například nemoc pokročila) před časem t, nejsou „ohroženi.,“Také, pokud subjekt v naší studii nechal své pozorování cenzurovat v době před časem t, nejsou také „ohroženi.“

V obvyklém módu, chceme postavit pravděpodobnost funkci (jaká je pravděpodobnost, že bychom pozorovali dat jsme vzhledem k proměnné a koeficienty) a pak optimalizovat, že dostat maximum-likelihood odhad.

pro každý diskrétní čas, kdy jsme pozorovali selhání subjektu j, je pravděpodobnost výskytu, vzhledem k tomu, že došlo k selhání, nižší. Suma je převzata ze všech ohrožených subjektů v době j.,

Všimněte si, že výchozí riziko λₒ vypadl! Vstřícný. Z tohoto důvodu je pravděpodobnost, kterou vytváříme, pouze částečná pravděpodobnost. Všimněte si také, že časy se vůbec neobjevují., Termín pro předmět j závisí pouze na tom, které subjekty jsou stále naživu v době j, což zase závisí pouze na pořadí, ve kterém jsou subjekty cenzurovány nebo pozorovány k selhání.

částečná pravděpodobnost je samozřejmě jen produktem těchto podmínek, jeden pro každé selhání, které pozorujeme (žádné podmínky pro cenzurované pozorování).,

přihlaste se částečné pravděpodobnost je pak

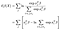
uchycení je provedeno pomocí standardních numerických metod, například v pythonu balíček statsmodels a variance-kovarianční matice pro odhady je dána (inverzní) Fisherova Informační Matice. Nic vzrušujícího.,

odhad základní funkce Survivor

Nyní, když jsme odhadli koeficienty,můžeme odhadnout funkci survivor. To se nakonec velmi podobá odhadu křivky Kaplan-Meier.

předpokládáme hlediska α indexovány jsem. V době, kdy jsem základní survivor křivka by se měla snížit o zlomek α představující podíl subjektů s rizikem, že se nepodaří v době, kdy jsem., Jinými slovy

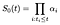
vypočítat maximální věrohodnosti odhad pro α, domníváme se, pravděpodobnost, že se příspěvek z tématu, které se nezdaří v době, kdy jsem a zvlášť příspěvek z těch, které jsou cenzurovány v době, kdy jsem.

Pro předmět, který selže v době, kdy jsem, pravděpodobnost je dána tím, že pravděpodobnost, že jsou naživu v době, kdy jsem menší pravděpodobnost, že jsou naživu v příštím okamžiku jsem+1. (Dočasně předpokládáme, že časy jsou objednány).,

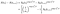
Pokud místo toho jsou cenzurovány v době, kdy jsem příspěvek je jen pravděpodobnost, že jsou naživu v době po i, tj., že ještě neumřel., Tohle je jen

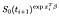
Tam je další termín z předmětů, které byly pozorovány (tj. pozorované selhání místo cenzurováno)., Log pravděpodobnost, že se stane

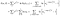
byl jsem trochu nedbalý o sledování koncových bodů (já vs. já+1), ale to bude všechno fungovat.

existují pouze α termíny pro subjekty, které jsme pozorovali k selhání., Rozlišování s ohledem na α-j a za předpokladu, že žádné vazby, můžeme získat příspěvek ze součtu na levé pouze pro předměty naživu v čase j, a jediný příspěvek z výrazu na pravé straně.,qual 0 znamená, že můžeme získat maximální věrohodnosti odhady pro α pomocí našeho odhadu pro β jako řešení několika rovnic, jeden pro každé téma, které bylo pozorováno selhání:

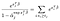
Rozšíření a Výhradami

je Tu mnohem více říci o Cox Proporcionálních Rizik modely, ale budu se snažit udržet věci stručně a jen zmínit pár věcí.,

například člověk může chtít zvážit regresory měnící čas, a to je možné.

další zásadní věc, kterou je třeba mít na paměti, je vynechána proměnná zkreslení. Ve standardní lineární regresi nejsou vynechané proměnné nespojené s regresory velkým problémem. To není pravda v analýze přežití. Předpokládejme, že v našich datech máme dvě stejně velké a vzorkované subpopulace s konstantní mírou nebezpečnosti, jedna je 0, 1 a druhá 0, 5. Zpočátku uvidíme vysokou míru nebezpečí (průměr, jen 0,3)., S postupem času populace s vysokou mírou nebezpečnosti opustí populaci a budeme pozorovat míru nebezpečí, která klesá směrem k 0.1. Pokud vynecháme proměnnou představující tyto dvě populace, naše základní míra nebezpečnosti bude celá zmatená.