α koeficient je nejvíce široce používaný postup pro odhad spolehlivosti v oblasti aplikovaného výzkumu. Jak uvedl Sijtsma (2009), jeho popularita je taková, že Cronbach (1951) byl citován jako referenční častěji než článek o objevu dvojité šroubovice DNA., Nicméně, jeho omezení jsou dobře známé (Lord a Novick, 1968; Cortina, 1993; Yang a Zelené, 2011), některé z nejdůležitějších jsou předpoklady nekorelované chyby, tau-rovnocennost a normality.
předpokladu nekorelované chyby (chyba se skóre pro každý pár položek, které je nekorelované), je hypotéza o Klasické testové Teorie (Lord a Novick, 1968), porušení, které mohou znamenat přítomnost komplexní multidimenzionální struktury, které vyžadují odhad postupy, které tuto složitost v úvahu (např. Tarkkonen a Vehkalahti, 2005; Green a Yang, 2015)., Je důležité vykořenit chybné přesvědčení, že α koeficient je dobrým ukazatelem jednosměrnosti, protože jeho hodnota by byla vyšší, pokud by stupnice byla jednosměrná. Ve skutečnosti je tomu přesně naopak, jak ukázala Sijtsma (2009), a jeho použití v takových podmínkách může vést k tomu, že spolehlivost bude silně nadhodnocena (Raykov, 2001). Proto je před výpočtem α nutné zkontrolovat, zda data odpovídají jednosměrným modelům.
předpoklad tau-ekvivalence (tj., stejné pravda skóre pro všechny zkušební položky, nebo rovno faktoru zatížení všech položek v faktoriál model) je podmínkou pro α se rovná koeficient spolehlivosti (Cronbach, 1951). Je-li předpoklad tau-ekvivalence je porušil pravda spolehlivosti hodnoty budou podceňována (Raykov, 1997; Graham, 2006) o částku, která se může lišit mezi 0,6 a 11,1% v závislosti na závažnosti porušení (Zelená a Yang, 2009a). Práce s daty, která jsou v souladu s tímto předpokladem, není v praxi obecně životaschopná (Teo a Fan, 2013); kongenerický model (tj.,, různé zatížení faktorů) je realističtější.
požadavek Na multivariantní normality je méně známý a ovlivňuje jak puntual odhad spolehlivosti a možnosti stanovení intervalů spolehlivosti (Dunn et al., 2014). Sheng a Sheng (2012) pozorovali, že v poslední době, kdy rozvody jsou asymetrické a/nebo leptokurtic, negativní zkreslení vzniká, když se koeficient α je vypočítána; podobné výsledky byly prezentovány Zelené a Yang (2009b) v analýze účinků non-normální rozdělení, odhad spolehlivosti., Studie šikmost problémů je více důležité, když vidíme, že v praxi badatelé obvykle pracují s asymetrické váhy (Micceri, 1989; Norton et al., 2013; Ho a Yu, 2014). Například Micceri (1989) odhadl, že asi 2/3 schopnosti a více než 4/5 psychometrických opatření vykazovaly alespoň mírnou asymetrii (tj. Navzdory tomu byl dopad špízu na odhad spolehlivosti málo studován.,
Vzhledem k hojné literatuře o omezení a předsudky z α koeficient (Revellovi a Zinbarg, 2009; Sijtsma, 2009, 2012; Cho a Kim, 2015; Sijtsma a van der Ark, 2015), vyvstává otázka, proč vědci i nadále používat α, když alternativní koeficienty existují, které překonání těchto omezení. Je možné, že nadbytek postupů pro odhad spolehlivosti vyvinutých v minulém století oscured diskusi. To by bylo ještě umocněno jednoduchostí výpočtu tohoto koeficientu a jeho dostupností v komerčních softwarech.,
obtížnost odhadu koeficientu spolehlivosti pxx spočívá v jeho definici PXX ‚ =σt2∕σx2, která zahrnuje skutečné skóre v čitateli rozptylu, pokud je to přirozeně nepozorovatelné. Koeficient α se snaží přiblížit tento nepozorovatelný rozptyl od kovariance mezi položkami nebo součástmi. Cronbach (1951) ukázal, že v nepřítomnosti tau-rovnocennost, α koeficient (nebo Guttman“s lambda 3, což odpovídá α) byla dobrá dolní mez sbližování., Tak, když jsou porušeny předpoklady problém se promítá do hledání nejlepší možné dolní mez; ve skutečnosti tento název je věnována Největší Dolní mez metody (GLB), což je nejlepší možné aproximace z teoretického úhlu (Jackson a Agunwamba, 1977; Woodhouse a Jackson, 1977; Shapiro a deset Berge, 2000; Sočan, 2000; deset Berge a Sočan, 2004; Sijtsma, 2009). Revelle a Zinbarg (2009) se však domnívají, že ω dává lepší nižší hranici než GLB., Existuje tedy nevyřešená debata o tom, která z těchto dvou metod dává nejlepší dolní hranici; kromě toho nebyla otázka normality vyčerpávajícím způsobem zkoumána, jak diskutuje současná práce.
ω Koeficienty
McDonald (1999) navrhl wt koeficient pro odhad spolehlivosti z faktorové analýzy rámec, který může být formálně vyjádřen jako:
Kde λj je načítání položky j, λj2 je zažít skupinovou položku j a ψ odpovídá jedinečnosti., Wt koeficient, včetně lambdy v jeho vzorce, je vhodná jak při tau-ekvivalence (tj. stejný faktor zatížení všech zkušebních položek) existuje (wt shoduje matematicky s α), a kdy položky s různými diskriminaci jsou přítomny v zastoupení konstrukt (tj. jiný faktor zatížení položky: podobných skupin měření). V důsledku toho wt koriguje podcenění α, když je porušen předpoklad Tau-ekvivalence (Dunn et al., 2014) a různé studie ukazují, že je to jedna z nejlepších alternativ pro odhad spolehlivosti (Zinbarg et al.,, 2005, 2006; Revelle a Zinbarg, 2009), ačkoli k dnešnímu dni jeho fungování v podmínkách špízu není známo.
Když existuje korelace mezi chybami, nebo existuje více než jeden latentní dimenze v datech, příspěvek každého rozměr celkového rozptylu bylo vysvětleno odhaduje, získání tzv. hierarchické ω (wh), což nám umožňuje opravit nejhorší nadhodnocení zaujatost α s vícerozměrných dat (viz Tarkkonen a Vehkalahti, 2005; Zinbarg et al., 2005; Revelle a Zinbarg, 2009)., Koeficienty wh a wt jsou ekvivalentní v jednosměrných datech, takže tento koeficient označíme jednoduše jako ω.
Největší Dolní mez (GLB)
Sijtsma (2009) ukazuje v sérii studií, které jeden z nejmocnějších odhady spolehlivosti je GLB—vyvodit, Woodhouse a Jackson (1977) z předpokladů Klasické testové Teorie (Cx = Ct + Ce)—inter-item kovarianční matice pozorovaných bod skóre Cx. To se porouchá do dvou částí: součet inter-item kovarianční matice pro položky skutečné výsledky Ct; a inter-item chyba kovarianční matice Ce (ten Berge a Sočan, 2004)., Jeho výraz je:
kde σx2 je test rozptylu a tr(Ce) se vztahuje na stopy inter-item chyba kovarianční matice, které se ukázalo tak obtížné odhadnout. Jedním z řešení bylo použití faktoriálních postupů, jako je analýza faktoru minimálního hodnocení (postup známý jako glb.fa). Více nedávno GLB algebraické (GLBa) postup byl vyvinut od algoritmus vymyslel Andreas Moltner (Moltner a Revellovi, 2015)., Podle Revellovi (2015a) tento postup nabývá formu, která je nejvíce věrný původní definice Jackson a Agunwamba (1977), a to má navíc tu výhodu, že zavedení vektoru hmotnost položky podle důležitosti (Al-Homidan, 2008).
Přes jeho teoretické přednosti, GLB byla velmi málo využívána, i když některé nedávné empirické studie ukázaly, že tento koeficient produkuje lepší výsledky než α (Lila et al., 2014) a α a ω (Wilcox et al., 2014)., Nicméně, v malé vzorky, za předpokladu normality, má tendenci přeceňovat skutečnou spolehlivost hodnotu (Shapiro a deset Berge, 2000); nicméně jeho fungování v rámci non-normálních podmínek zůstává neznámý, konkrétně při rozdělování položek jsou asymetrické.
Vzhledem k tomu, že koeficienty jsou definovány výše, a předsudky a omezení každého, předmětem této práce je zhodnocení spolehlivosti těchto koeficientů v přítomnosti asymetrické položky, rovněž s ohledem na předpoklad tau-rovnocennost a velikost vzorku.,
Metody
Generování Dat
údaje byly získány pomocí R (R Development Core Team, 2013) a RStudio (Racine, 2012) software, po faktoriál model:
kde Xij je simulované reakci na téma, které jsem v bodě j, λjk je načítání položky j ve Faktoru k (který byl vygenerován unifactorial model); Fk je latentní faktor vytvořené standardizované normální rozdělení (průměr 0 a rozptyl 1), a ej je náhodná chyba měření každé položky také v návaznosti na standardizované normální rozdělení.,
Asymetrické položky: Standardní normální Xij byly transformovány generovat non-normální rozdělení použití postupu navrženého Headrick (2002) použití pátého řádu polynomická transformace:
Simulované Podmínky
posoudit výkonnost spolehlivost koeficienty (α, ω, GLB a GLBa) pracovali jsme se třemi velikost vzorku (250, 500, 1000), dva zkušební velikostech: krátké (6 položek) a dlouhé (12 položek), dvě podmínky tau-ekvivalence (jeden s tau-rovnocennost a jeden bez, tj.,, kongenerické) a progresivní začlenění asymetrických položek (ze všech položek, které jsou normální pro všechny položky, které jsou asymetrické). V krátkodobém testu spolehlivosti byla stanovena na 0.731, které se v přítomnosti tau-ekvivalence je dosaženo s šesti položky s faktorem zatížení = 0.558; zatímco podobných skupin model je získán tím, že nastavení faktoru zatížení na hodnoty 0.3, 0.4, 0.5, 0.6, 0.7, a 0,8 (viz Dodatek I). Při dlouhém testu 12 položek byla spolehlivost nastavena na 0.,845 se stejnými hodnotami jako v krátkém testu pro ekvivalenci tau i pro kongenerický model (v tomto případě existovaly dvě položky pro každou hodnotu lambda). Tímto způsobem bylo v každém případě simulováno 120 podmínek se 1000 replikami.
Analýza Dat
hlavní analýzy byly provedeny pomocí Psychologie (Revellovi, 2015b) a GPArotation (Bernaards a Jennrich, 2015) pakety, které umožňují α a ω být odhadnuta. Pro odhad GLB byly použity dva počítačové přístupy: glb. fa (Revelle, 2015a) a glb.,algebraický (Moltner a Revelle, 2015), druhý pracoval autory jako Hunt a Bentler (2015).
abychom mohli vyhodnotit přesnost různých odhadů při obnovení spolehlivosti, vypočítali jsme kořenový Střední čtverec chyby (RMSE) a zkreslení. První je průměr rozdílů mezi odhadovanou a simulované spolehlivost a je formován jako:
kde ρ^ je odhadovaná spolehlivost pro každý koeficient, ρ simulované spolehlivost a Nr počet repliky., % Zkreslení je chápán jako rozdíl mezi tím odhadované spolehlivosti a simulované spolehlivost a je definována jako:
V obou indexů, větší hodnota, tím větší je nepřesnost odhadu, ale na rozdíl od RMSE, bias může být pozitivní nebo negativní; v tomto případě, další informace by být získány, zda koeficient je podceňování nebo přeceňování simulované spolehlivost parametr., Následující doporučení Hoogland a Boomsma (1998) hodnoty RMSE < 0,05 a % zkreslení < 5% byly považovány za přijatelné.
Výsledky
hlavní výsledky lze vidět v Tabulce 1 (6 položek) a Tabulce 2 (12 položek). Tyto ukazují RMSE a % zkreslení koeficientů v tau-rovnocennost a podobných skupin podmínky, a jak šikmost testovací distribuce se zvyšuje s postupným začleněním asymetrické předměty.
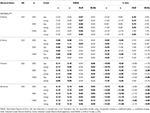
Tabulka 1., RMSE a zaujatost s Tau-ekvivalence a kongenerický stav pro 6 položek, tři velikosti vzorku a počet zkosených položek.
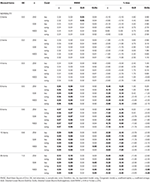
Tabulka 2. RMSE a zaujatost s Tau-ekvivalence a kongenerický stav pro 12 položek, tři velikosti vzorku a počet zkosených položek.
Pouze za podmínek tau-rovnocennost a normality rozdělení (šikmost < 0.2) je zjištěno, že α koeficient odhady simulované spolehlivost správně, jako ω., V kongenerickém stavu ω koriguje podcenění α. GLB i GLBa představují pozitivní zkreslení v normálnosti, avšak GLBa vykazuje přibližně ½ % zkreslení než GLB (viz tabulka 1). Pokud vezmeme v úvahu velikost vzorku, pozorujeme, že jak se velikost testu zvyšuje, pozitivní zkreslení GLB a GLBa se snižuje, ale nikdy nezmizí.
V asymetrické podmínky, můžeme vidět v Tabulce 1, že obě α a ω představuje nepřijatelné výkon s rostoucí RMSE a podhodnocování, které mohou dosáhnout zkreslení > 13% pro α koeficient (mezi 1 a 2% nižší, pro ω)., Koeficienty GLB a GLBa představují nižší RMSE, když se zvyšuje zkušební špíz nebo počet asymetrických položek (viz tabulky 1, 2). GLB koeficient představuje lepší odhady, když test šikmosti hodnota testu je kolem 0.30; GLBa je velmi podobné, představuje lepší odhady než ω s test šikmosti hodnotu kolem 0.20 nebo 0,30. Nicméně, když šikmost hodnota se zvyšuje nebo 0,60 0,50, GLB představuje lepší výkon než GLBa. Test velikosti (6 nebo 12 předmětů) má mnohem důležitější vliv než velikost vzorku na přesnost odhadů.,
Diskuse
V této studii čtyři faktory byly zmanipulovány: tau-rovnocennost nebo podobných skupin model, velikost vzorku (250, 500 a 1000), počet zkušebních položek (6 a 12) a počet asymetrické předměty (od 0 asymetrické položky všechny položky jsou asymetrické) s cílem posoudit odolnost přítomnost asymetrické data ve čtyřech spolehlivosti koeficientů analyzovány. Tyto výsledky jsou popsány níže.,
V podmínkách tau-rovnocennost, α a ω koeficienty konvergují, nicméně v nepřítomnosti tau-ekvivalence (podobných skupin), ω vždy představuje lepší odhady a menší RMSE a % zkreslení než α. V tomto realističtější stavu, proto (Zelená a Yang, 2009a; Yang a Zelené, 2011), α stává negativně zaujatý spolehlivost odhad (Graham, 2006; Sijtsma, 2009; Cho a Kim, 2015) a ω je vždy vhodnější, aby α (Dunn et al., 2014). V případě porušení předpokladu normality, ω je nejlepší odhad všech koeficientů vyhodnocena (Revellovi a Zinbarg, 2009).,
Otočil se k velikosti vzorku, pozorujeme, že tento faktor má malý efekt v rámci normality nebo mírný odklon od normality: RMSE a zaujatost snižovat, jelikož velikost vzorku zvyšuje. Nicméně lze říci, že pro tyto dva koeficienty, s velikostí vzorku 250 a normálností, získáváme relativně přesné odhady (Tang a Cui, 2012; Javali et al., 2011)., Pro GLB a GLBa koeficienty, jako velikost vzorku zvyšuje RMSE a předsudky mají tendenci snižovat; nicméně se udržet pozitivní zaujatost pro podmínku normality i s velkými vzorku o velikosti 1000 (Shapiro a deset Berge, 2000; deset Berge a Sočan, 2004; Sijtsma, 2009).
Pro test velikosti můžeme obecně pozorovat vyšší RMSE a zaujatost s 6 položek, než s 12, což naznačuje, že vyšší počet položek, tím nižší RMSE a zaujatost estimátorů (Cortina 1993). Obecně je trend udržován pro 6 i 12 položek.,
Když se podíváme na efekt postupně zahrnující asymetrické položek do datového souboru, můžeme pozorovat, že koeficient α je vysoce citlivý na asymetrické předměty; tyto výsledky jsou podobné těm, které najdete Sheng a Sheng (2012) a Zelenou a Yang (2009b). Koeficient ω představuje podobné hodnoty RMSE a zkreslení jako hodnoty α, ale o něco lepší, a to i při ekvivalenci tau. Bylo zjištěno, že GLB a GLBa představují lepší odhady, když se zkušební špíz odchyluje od hodnot blízkých 0.
vzhledem k tomu, že v praxi je běžné najít asymetrická data (Micceri, 1989; Norton et al.,, 2013; Ho a Yu, 2014), sijtsma návrh (2009) použití GLB jako odhad spolehlivosti se jeví jako opodstatněné. Jiní autoři, jako Revellovi a Zinbarg (2009) a Zelené a Yang (2009a), doporučujeme použít ω, nicméně tento koeficient vyráběny pouze dobré výsledky ve stavu normality, nebo s nízkým podílem šikmost položky. V každém případě tyto koeficienty představovaly větší teoretické a empirické výhody než α. Nicméně, doporučujeme vědci studovat nejen přesné odhady, ale také využít intervalový odhad (Dunn et al., 2014).,
tyto výsledky jsou omezeny na simulované podmínky a předpokládá se, že neexistuje žádná korelace mezi chybami. To by bylo nezbytné provést další výzkum, aby zhodnotila fungování různých spolehlivosti koeficientů s více komplexní multidimenzionální struktury (Reise, 2012; Zelené a Yang, 2015) a v přítomnosti ordinální a/nebo kategoriálních dat, ve kterém nedodržení předpokladu normality je normou.
závěr
při normálním rozložení celkového skóre testu (tj.,, všechny položky jsou obvykle distribuovány) ω by měla být první volbou, následovaná α, protože se vyhýbají problémům s nadhodnocením prezentovaným GLB. Nicméně, pokud je nízká nebo střední zkušební špíz GLBa by měla být použita. GLB se doporučuje, pokud je podíl asymetrických položek vysoký, protože za těchto podmínek není vhodné používat jak α, tak ω jako odhady spolehlivosti, bez ohledu na velikost vzorku.
Autor Příspěvky
Vývoj myšlenky výzkumu a teoretického rámce (JA). Konstrukce metodického rámce (IT, JA)., Vývoj syntaxe jazyka R (IT, JA). Analýza dat a interpretace dat (IT, JA). Diskuse o výsledcích ve světle současného teoretického zázemí (JA, IT). Příprava a psaní článku (JA, IT). Obecně oba autoři přispěli k rozvoji této práce stejně.,
finanční Prostředky
první autor zveřejněny obdržení finanční podporu výzkumu, autorství a/nebo zveřejnění tohoto článku: je TO získal finanční podporu z Chilské Národní Komisi pro Vědecký a Technologický Výzkum (CONICYT) „Becas Chile“ Doktorské Stipendijní program (Grant č.: 72140548).
Prohlášení o střetu zájmů
autoři prohlašují, že výzkum byl proveden bez jakýchkoli obchodních nebo finančních vztahů, které by mohly být chápány jako potenciální střet zájmů.
Cronbach, L. (1951)., Koeficient alfa a vnitřní struktura testů. Psychometrika 16, 297-334. doi: 10.1007 / BF02310555
CrossRef Full Text / Google Scholar
McDonald, R. (1999). Teorie testů: jednotná léčba. Mahwah, NJ: Lawrence Erlbaum Associates.
Google Scholar
R Development Core Team (2013). R: jazyk a prostředí pro statistické výpočty. Vídeň: R Foundation for Statistical Computing.
Raykov, T. (1997)., Scale reliability, cronbach“s coefficient alpha, and violations of essential tau- equivalence with fixed congeneric components. Multivariate Behav. Res. 32, 329–353. doi: 10.1207/s15327906mbr3204_2
PubMed Abstract | CrossRef Full Text | Google Scholar
Raykov, T. (2001). Bias of coefficient alpha for fixed congeneric measures with correlated errors. Appl. Psychol. Meas. 25, 69–76. doi: 10.1177/01466216010251005
CrossRef Full Text | Google Scholar
Revelle, W. (2015b). Package „psych.,“K dispozici online na adrese: http://org/r/psych-manual.pdf
Shapiro, a.A ten Berge, J. M. F. (2000). Asymptotická předpojatost analýzy minimálních stopových faktorů, s aplikacemi s největší nižší vazbou na spolehlivost. Psychometrika 65, 413-425. doi: 10.1007/BF02296154
CrossRef Plný Text | Google Scholar
deset Berge, J. M. F., a Sočan, G. (2004). Největší nižší vazba na spolehlivost testu a hypotézu jednosměrnosti. Psychometrika 69, 613-625. doi: 10.,1007 / BF02289858
CrossRef Full Text / Google Scholar
Woodhouse, B., and Jackson, P. H. (1977). Nižší hranice pro spolehlivost celkového skóre při testu složeném z nehomogenních položek: II: vyhledávací postup pro nalezení největší dolní hranice. Psychometrika 42, 579-591. DOI: 10.1007/BF02295980
CrossRef Full Text | Google Scholar
Dodatek i
r syntax pro odhad koeficientů spolehlivosti z pearsonových korelačních matic., Korelace hodnot mimo diagonálu jsou vypočteny vynásobením faktorem načítání položek: (1) tau-ekvivalentní model jsou si všechny rovny 0.3114 (λiλj = 0.558 × 0.558 = 0.3114) a (2) podobných skupin model se liší jako funkce různých faktor zatížení (např. prvek matice a1, 2 = λ1λ2 = 0.3 × 0.4 = 0.12). V obou příkladech je skutečná spolehlivost 0,731.
> omega(Čr,1)$alpha # standardizované Cronbach“s α
0.731
> omega(Čr,1)$omega.tot # koeficient ω celkem
0.,731
> glb.fa(Cr)$glb # GLB factorial procedure
0.731
> glb.algebraic(Cr)$glb # GLB algebraic procedure
0.731
> omega(Cr,1)$alpha # standardized Cronbach“s α
0.717
> omega(Cr,1)$omega.tot # coefficient ω total
0.731
> glb.fa(Cr)$glb # GLB factorial procedure
0.754
> glb.algebraic(Cr)$glb # GLB algebraic procedure
0.731