„já jsem v každém případě, jsem přesvědčen, že nemá házet kostky.,“
~ Albert Einstein
- Náhodné Proměnné
- Diskrétní Náhodné Proměnné,
- a Spojité Náhodné Proměnné
- Smíšené Náhodné Proměnné
- Kumulativní Distribuční Funkce (CDF)
- Funkce Hustoty Pravděpodobnosti (PDF)
- Interaktivní CDF/PDF Příklad
Náhodné Proměnné:

Řekněme, že vzít minci z kapsy a hodit ji do vzduchu. Zatímco to proletí vesmírem, co byste mohli říci o jeho budoucnosti?
přistane hlavou nahoru? Orel?, Více než to, jak dlouho zůstane ve vzduchu? Kolikrát se to odrazí? Jak daleko od místa, kde poprvé narazí na zem, bude konečně odpočívat? Když na to přijde, dopadne to někdy na zem? Přišel jste někdy odpočívat?
u některých takových otázek se můžeme a můžeme spokojit s odpověďmi dlouho před pozorováním; jsme si jisti, že gravitace bude držet a mince přistane. Ale pro ostatní nemáme jinou možnost, než držet úsudek a mluvit nejasněji, pokud chceme říci něco užitečného o budoucnosti vůbec.,
jako vědci je samozřejmě naším úkolem říci něco užitečného (nebo přinejmenším autoritativního…), zatímco metaforické mince důležitého fyzického systému jsou stále ve vzduchu. Hlavy nebo ocasy mohou být dokonce otázkou života nebo smrti. Našimi mincemi mohou být například různé možné průtoky chladicí kapaliny nebo masy uranu v jaderné elektrárně. Velmi nám záleží na tom, jaké jsou naše šance, že místo roztavení dostaneme vířící turbíny.,
přísnému deterministovi byly všechny takové sázky vypořádány dlouho předtím, než byla nějaká mince, metaforická nebo ne, někdy ražena; prostě to ještě nevíme. Kdybychom věděli jen síly aplikované při hodu mincí, jeho přesné rozložení hmotnosti, různé minutové pohyby vzduchu v místnosti… Kdybychom to všechno věděli, pak bychom věděli, že konkrétní hod mincí má 100% šanci přistát tak, jak přistane, a nulovou šanci na jakýkoli jiný výsledek.
ale my samozřejmě často chybí i zmíněný zlomek takového poznání světa., Navíc, zdá se, na mimořádně malé váhy, že přísná deterministé jsou naprosto špatně; neexistuje žádný způsob, jak předpovědět, kdy, například, atom uranu se rozdělí, a pokud se taková událost má vliv na větší svět tak, že makro událost je skutečně nepředvídatelné. Některé výsledky jsou skutečně ve vzduchu, neklidné, dokud nejsou součástí minulosti.
abychom se s touto realitou vyrovnali a mohli nějakým užitečným způsobem popsat budoucí stavy systému, používáme náhodné proměnné., Náhodná proměnná je prostě funkce, která spojuje každý možný fyzický výsledek systému s nějakým jedinečným, reálným číslem. Jako takové existují tři druhy náhodných proměnných: diskrétní, spojité a smíšené. V následujících částech budou tyto kategorie stručně diskutovány a budou uvedeny příklady.
diskrétní náhodné proměnné:
zvažte náš hod mincí znovu. Mohli bychom mít hlavy nebo ocasy jako možné výsledky. Pokud bychom definovali proměnnou, x, jako počet hlav v jednom hodu, pak x může být 1 nebo 0, nic jiného., Taková funkce, x, by byla příkladem diskrétní náhodné proměnné. Takové náhodné proměnné mohou mít pouze diskrétní hodnoty. Dalšími příklady by byly možné výsledky těhotenského testu nebo počet studentů ve třídě.
spojité náhodné proměnné:
zpět k hodu mincí, co kdybychom chtěli popsat vzdálenost mezi tím, kde naše mince spočívala a kde poprvé dopadla na zem. Tato vzdálenost, x, by byla spojitá náhodná proměnná, protože by mohla nabývat nekonečného počtu hodnot v nepřetržitém rozsahu reálných čísel., Mince by mohla cestovat 1 cm, nebo 1,1 cm, nebo 1,11 cm, nebo na a na. Dalšími příklady spojitých náhodných proměnných by byla hmotnost hvězd v naší galaxii, pH oceánských vod nebo doba pobytu nějakého analytu v plynovém chromatografu.
smíšené náhodné proměnné:
smíšené náhodné proměnné mají diskrétní i spojité složky. Takové náhodné proměnné se zřídka vyskytují. Pro možný příklad, ačkoli, můžete být měření hmotnosti vzorku a rozhodnout, že každá hmotnost měřená jako záporná hodnota bude mít hodnotu 0., Tímto způsobem má náhodná proměnná diskrétní komponentu na x = 0 a spojitou složku, kde x > 0.
Kumulativní Distribuční Funkce (CDF):
otázka, samozřejmě, otázka, jak nejlépe matematicky popsat (a vizuálně zobrazení) náhodné veličiny. Pro tyto úkoly používáme funkce hustoty pravděpodobnosti (PDF) a funkce kumulativní hustoty (CDF). Vzhledem k tomu, že CDFs je pro diskrétní i spojité náhodné proměnné jednodušší než pdf, nejprve vysvětlíme CDFs.
zvažte házení spravedlivých 6-sidded kostek., Měli bychom 1 v 6 šanci získat některou z možných hodnot náhodné proměnné (1, 2, 3, 4, 5, nebo 6). Pokud tyto možné hodnoty vykreslíme na ose x a vykreslíme pravděpodobnost měření každé konkrétní hodnoty, x nebo jakékoli hodnoty menší než x na ose y, budeme mít CDF náhodné proměnné.
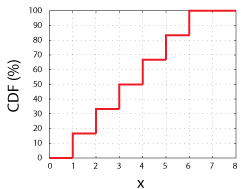
CDF pro spravedlivé 6-Sidded kostky. Všimněte si, že každý krok je výška 16,67%, nebo 1 v 6.
tato funkce, CDF (x), nám jednoduše říká šance na měření jakékoli hodnoty až do x a včetně., Jako takové musí mít všechny CDFs všechny tyto vlastnosti:
- a CDF se musí rovnat 0, když x = -∞, a přístup 1 (nebo 100%), když se x blíží +∞. Jednoduše řečeno, ze všech možných výsledků, musí být výsledek; možnost házet se šesti kostkami a získání hodnot mezi -∞ a ∞ je 100%.
- sklon CDF musí být vždy roven nebo větší než nula. Zvažte například šanci hodit 6-sidded kostky (spravedlivé nebo ne) a získat hodnotu mezi 0 a 4., Tu šanci nemůže být více než šance na získání hodnoty mezi 0 a 5, protože šance, 1, 2, nebo 3 přistání lícem nahoru, jsou, samozřejmě, vždy bude nějaký zlomek šance, jak se dostat 1, 2, 3, nebo 4.
pro příklad spojité náhodné proměnné ukazuje následující aplet normálně distribuovaný CDF.,div>
| -5 | 5 |
| x | |
This important distribution is discussed elsewhere., Jednoduše si všimněte, že vlastnosti CDF popsané výše a vysvětleno pro diskrétní náhodné proměnné hold pro spojité náhodné proměnné, jakož.
pro více intuitivních příkladů vlastností CDFs, viz interaktivní příklad níže. Také interaktivní grafy mnoha dalších CDFs důležité pro oblast statistiky a používané na tomto webu lze nalézt zde.
Funkcí Hustoty Pravděpodobnosti (PDF):
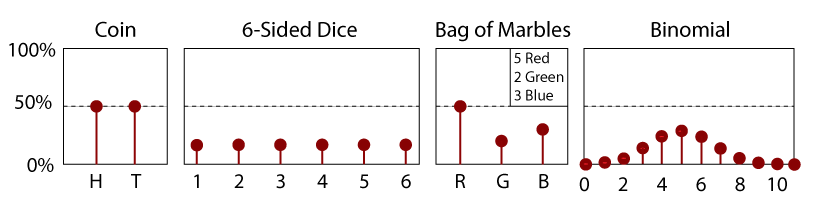
PDF pro Veletrh 6-Sidded Kostky.
PDF je jednoduše derivát CDF., PDF je tedy také funkcí náhodné proměnné x a její velikost bude určitým ukazatelem relativní pravděpodobnosti měření určité hodnoty. Vzhledem k tomu, že se jedná o sklon CDF, musí být PDF vždy pozitivní; neexistují žádné negativní šance na jakoukoli událost. Kromě toho a podle definice se plocha pod křivkou PDF (x) mezi – ∞ A x rovná jeho CDF (x). Jako taková oblast mezi dvěma hodnotami x1 a x2 dává pravděpodobnost měření hodnoty v tomto rozsahu.
následující aplet ukazuje příklad PDF pro normálně distribuovanou náhodnou proměnnou, x.,
Normal PDF
|
x:
| mean:
| stdev:
| f(x):
|
|
Notice, when the mean and standard deviations are equal, how the PDF correlates with the normal CDF in the section above., také zvažte rozdíl mezi spojitým a diskrétním PDF. Zatímco diskrétní PDF (například výše uvedené pro kostky) vám dá šance na získání konkrétního výsledku, pravděpodobnosti s spojitými PDF jsou záležitostí rozsahu, nikoli diskrétních bodů. Například, tam je jasně 1 v 6 (16.6%) šance na válcování 3 na kostky, jak je vidět v jeho PDF. Ale jaké jsou liché měření přesně nuly s náhodnou proměnnou, která má normální PDF a průměr nuly, jak je uvedeno výše? I když je to hodnota, kde je PDF největší, šance na měření přesně 0.00000..,. je, možná počítadlo intuitivně, nula. Šance na měření konkrétního náhodného čísla na nekonečnou přesnost jsou ve skutečnosti nulové. s kontinuálním PDF se můžete místo toho zeptat, jaké jsou šance, že změříte mezi dvěma hodnotami, abyste získali pravděpodobnost, která je větší než nula. K nalezení této pravděpodobnosti jednoduše použijeme CDF naší náhodné proměnné., Protože CDF nám říká, liché měření hodnota nebo něco nižší, než hodnoty, najít pravděpodobnost, že měření mezi dvěma hodnotami, x1 a x2 (kde x1 > x2), budeme prostě muset vzít hodnotu CDF na x1 a odečíst od ní hodnotu CDF na x2. Například, s použitím normální CDF v apletu výše (s μ=0 a σ=1), pokud bychom chtěli znát pravděpodobnost, že měření mezi 0,01 a 0,02 jsme najít CDF(x=0.1)=53.9828% a CDF(x=0.2)=57.9260%. Pak rozdíl, CDF (0.2) – CDF(0.1), nám dává pravděpodobnost asi 3.9% měření x mezi 0.1 a 0.2., pro více intuitivní, vizuální příklady vlastností PDF, viz interaktivní příklad níže. Také interaktivní grafy mnoha důležitých PDF používaných na tomto webu lze vidět zde. |
|||||||||||||||||