8.1 historický příklad
Ve své knize, Se Dvou Nových Věd, Galileo Galilejské (1564-1642) uvádí několik argumentů, možno prokázat, že tam může být žádná taková věc jako skutečná nekonečna nebo skutečné drobnosti. Jeden z jeho argumentů lze rekonstruovat následujícím způsobem. Galileo navrhuje, že si vezmeme jako předpoklad, že tam je skutečné nekonečno přirozených čísel (přirozená čísla jsou celá kladná čísla od 1):
{1, 2, 3, 4, 5, 6, 7, ….,}
navrhuje také, abychom brali jako předpoklad, že existuje skutečné nekonečno čtverců přirozených čísel.
{1, 4, 9, 16, 25, 36, 49, ….}
nyní, důvody Galileo, všimněte si, že tyto dvě skupiny (dnes bychom jim říkali „sady“) mají stejnou velikost. Můžeme to vidět, protože vidíme, že mezi oběma skupinami existuje korespondence jedna ku jedné.,
| {1, | 2, | 3, | 4, | 5, | 6, | 7, ….,div> | |
| {1, | 4, | 9, | 16, | 25, | 36, | 49, …} |
Pokud můžeme přiřadit každé přirozené číslo s jedním a pouze jedním náměstí číslo, a pokud můžeme spojit každý čtvereční číslo s jedním a pouze jedním přirozené číslo, pak tyto sady musí mít stejnou velikost.,
ale počkejte chvíli, říká Galileo. Samozřejmě existuje mnohem více přirozených čísel, než jsou čtvercová čísla. To znamená, že každé čtvercové číslo je v seznamu přirozených čísel, ale mnoho přirozených čísel není v seznamu čtvercových čísel. Následující čísla jsou v seznamu přirozených čísel, ale ne v seznamu čtvercových čísel.
{2, 3, 5, 6, 7, 8, 10, ….,}
Tak, Galileo důvodů, pokud existuje mnoho čísel ve skupině přirozených čísel, které nejsou ve skupině náměstí čísel, a pokud tam jsou žádná čísla ve skupině náměstí čísel, která nejsou v naturals čísla, pak přirozených čísel je větší než druhá odmocnina čísla. A pokud je skupina přirozených čísel větší než skupina čtvercových čísel, pak přirozená čísla a čtvercová čísla nejsou stejné velikosti.,
Jsme dosáhli dva závěry: množina přirozených čísel a množina náměstí čísel jsou stejné velikosti, a množina přirozených čísel a množina náměstí čísla nejsou stejné velikosti. To je rozporuplné.
Galileo tvrdí, že důvodem, proč jsme dosáhli rozporu, je to, že jsme předpokládali, že existují skutečné Infinity. Dochází proto k závěru, že neexistují žádné skutečné Infinity.
8.2 nepřímé důkazy
naše logika ještě není dostatečně silná, aby dokázala některé platné argumenty. Zvažte následující argument jako příklad.,
(p→(QvR))
Q
r
p
tento argument vypadá platně. Podle prvního předpokladu víme: pokud P byla pravda, pak by to tak bylo (Q v R) být pravda. Ale pak buď Q nebo R nebo obojí by byla pravda. A ve druhé a třetí místnosti víme: Q je nepravdivé a R je nepravdivé. Takže to nemůže být, že (Q v R) je pravda, a tak to nemůže být, že P je pravda.
můžeme zkontrolovat argument pomocí tabulky pravdy. Náš stůl bude složitý, protože jeden z našich předpokladů je složitý.,
In any kind of situation in which all the premises are true, the conclusion is true., To znamená, že prostory jsou pravdivé pouze v posledním řádku. Pro tento řádek je závěr také pravdivý. Takže to je platný argument.
ale trvat minutu a pokusit se dokázat tento argument. Začínáme

a nyní jsme zastaveni. Nemůžeme použít žádná z našich pravidel. Zde je platný argument, že jsme neudělali náš systém uvažování dostatečně silný, abychom dokázali.
existuje několik způsobů, jak tento problém napravit a učinit náš systém uvažování dostatečně silným., Jedním z nejstarších řešení je zavedení nové důkazní metody, tradičně nazývané „reductio ad absurdum“, což znamená snížení absurdity. Tato metoda se také často nazývá „nepřímým důkazem“nebo“ nepřímým odvozením“.
myšlenka je, že předpokládáme popření našeho závěru a pak ukážeme, že rozpor vede. Rozpor se projevuje, když prokážeme nějakou větu a její negaci. To může být jakákoli věta. Jde o to, že vzhledem k principu bivalence jsme museli prokázat něco falešného. Pokud je Ψ pravda, pak Ψ je nepravdivé; a pokud je Ψ pravda, pak Ψ je nepravdivé., Nepotřebujeme vědět, co je nepravdivé( Ψ nebo Ψ); stačí vědět, že jeden z nich musí být.
nezapomeňte, že jsme vybudovali náš logický systém tak, aby nemohl vytvářet faleš ze skutečných výroků. Zdrojem lži, kterou vytváříme v nepřímém odvození, musí být tedy nějaká faleš, kterou jsme přidali k našemu argumentu. A to, co jsme přidali k našemu argumentu, je popření závěru. Závěr tedy musí být pravdivý.,
tvar argument je jako toto:

Tradičně, předpoklad pro nepřímé odvození se také běžně nazývá „předpoklad pro reductio“.
jako konkrétní příklad můžeme prokázat náš matoucí případ.

předpokládali jsme odmítnutí našeho závěru na řádku 4. Závěr, o kterém jsme věřili, že je správný, byl P, a popření tohoto je P. v řádku 7 jsme prokázali R., Technicky jsme v tomto bodě hotovi, ale rádi bychom byli laskaví ke každému, kdo se snaží pochopit náš důkaz, takže opakujeme řádek 3 tak, aby věty R A R byly vedle sebe, a je velmi snadné vidět, že se něco pokazilo. To znamená, že pokud jsme prokázali jak R, tak R, pak jsme prokázali něco falešného.
naše úvaha nyní jde takto. Co se pokazilo? Řádek 8 je správné použití opakování; řádek 7 pochází ze správného použití Modus tollendo ponens; řádek 6 ze správného použití Modus ponens; řádek 5 ze správného použití dvojité negace., Takže jsme v našem uvažování neudělali chybu. Použili jsme linky 1, 2 a 3, ale to jsou prostory, které jsme se dohodli předpokládat, jsou správné. To ponechává řádek 4. To musí být zdrojem mého rozporu. Musí to být falešné. Pokud je řádek 4 falešný, pak P je pravda.
někteří lidé považují nepřímé důkazy za méně silné než přímé důkazy. Existuje mnoho a složitých důvodů. Ale, pro naši návrhovou logiku, žádný z těchto důvodů neplatí. Je to proto, že je možné prokázat, že naše návrhová logika je konzistentní., To znamená, že je možné dokázat, že naše propoziční logika nemůže dokázat klam, pokud jeden nejprve zavede klam do systému. (Obecně není možné prokázat, že silnější a pokročilejší logické nebo matematické systémy jsou konzistentní, zevnitř těchto systémů; například v aritmetice nelze dokázat, že aritmetika je konzistentní.) Vzhledem k tomu, že si můžeme být jisti konzistencí výrokové logiky, můžeme si být jisti, že v naší výrokové logice je nepřímým důkazem dobrá forma uvažování., Víme, že pokud dokážeme lež, musíme dát lež; a pokud jsme přesvědčeni o všech dalších předpokladů (tj. prostor) důkaz s výjimkou předpoklad pro nepřímé odvození, pak si můžeme být jisti, že tento předpoklad pro nepřímé odvození musí být zdroj lež.
zde je vyžadována poznámka o terminologii. Slovo „rozpor“ se ve většině logických diskusí používá nejednoznačně. Může to znamenat situaci, jakou vidíme výše, kde se uplatňují dvě věty a tyto věty nemohou být pravdivé., Nebo to může znamenat jednu větu, která nemůže být pravdivá. Příkladem takové věty je (P^P)., Pravdivostní tabulky pro tato věta je:
| P | P | (P ^ P) |
|---|---|---|
| T | F | F |
| F | T | F |
Tedy, tento druh trestu může nikdy být pravda, bez ohledu na význam P.,
abychom se vyhnuli nejednoznačnosti, v tomto textu budeme vždy nazývat jedinou větu, která nemůže být pravdivá, „protichůdnou větou“. Takže (P^P) je protichůdná věta. Situace, kdy se tvrdí dvě věty, které nemohou být pravdivé, se nazývají „rozpor“.
8.3 náš příklad a další příklady
nyní můžeme rekonstruovat verzi argumentu Galileo. Použijeme následující klíč.
P: existují skutečné Infinity (včetně přirozených čísel a čtvercových čísel).,
Q: mezi přirozenými čísly a čtvercovými čísly existuje korespondence jedna ku jedné.
R: Velikost sady přirozených čísel a velikost sady čtvercových čísel jsou stejné.
S: všechna čtvercová čísla jsou přirozená čísla.
t: některá přirozená čísla nejsou čtvercová čísla.
U: existuje více přirozených čísel než čtvercová čísla.,
S tímto klíčem, argument bude přeloženo:
(P→Q)
(Q→R),
(P→(S^T))
((S^T)→U),
(U→R)
P
A můžeme dokázat, že to je platný argument pomocí nepřímé odvození:

Na řádku 6 jsme předpokládali, že P, protože Galileo věřil, že P a jehož cílem je prokázat, že P. to znamená, Že on věřil, že tam jsou žádné skutečné nekonečna, a tak předpokládal, že to bylo nesprávné domnívat se, že to není případ, že neexistují žádné skutečné nekonečna. Tato lež povede k dalším falešným věcem a vystaví se.,
pro zájemce: Galileo dospěl k závěru, že neexistují žádné skutečné Infinity, ale existují potenciální Infinity. Odůvodnil tedy, že tomu tak není, že existují všechna přirozená čísla (v jistém smyslu „existují“), ale je pravda, že byste mohli navždy počítat přirozená čísla. Mnoho filozofů před a po Galileo držel tento názor; to je podobné názoru držel Aristoteles, který byl důležitým logik a filozof psaní téměř dva tisíce let před Galileo.,
Všimněte si, že v argumentu, jako je tento, jste mohli důvodu, že není předpoklad pro nepřímé odvození, ale spíše ten prostor byl zdrojem rozporu. Dnes se většina matematiků domnívá, že se jedná o Galileův argument. Logik a matematik Georg Cantor (1845-1918), vynálezce teorie, tvrdil, že nekonečné množiny mohou mít vlastní podmnožiny stejné velikosti., To znamená, že Cantor popřel předpoklad 4 výše: i když všechna čtvercová čísla jsou přirozená čísla, a ne všechna přirozená čísla jsou čtvercová čísla, není tomu tak, že tyto dvě sady mají různou velikost. Cantor však přijal předpoklad 2 výše, a proto věřil, že velikost sady přirozených čísel a velikost sady čtvercových čísel je stejná. Dnes, pomocí Cantorovy úvahy, matematici a logici studují Nekonečno a vyvinuli velké množství znalostí o povaze nekonečna. Pokud vás to zajímá, viz bod 17.5.,
uvažujme o dalším příkladu pro ilustraci nepřímé derivace. Velmi užitečná sada vět se dnes nazývá „de Morganovy věty“ po logikovi Augustovi De Morganovi (1806-1871). Nemůžeme stát tyto plně do kapitoly 9, ale můžeme se stát jejich ekvivalent v angličtině: DeMorgan pozorováno, že (PvQ) a (P^Q) jsou ekvivalentní, a také to, že (P^Q) a (PvQ) jsou ekvivalentní. Vzhledem k tomu by měla být věta našeho jazyka, která ((PvQ)→(P^Q)). Dokažme to.
celý vzorec je podmíněný, takže použijeme podmíněnou derivaci., Náš důkaz tedy musí začít:
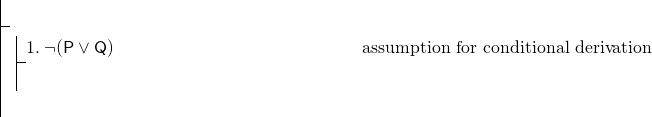
pro dokončení podmíněného odvození musíme prokázat (P^Q). Toto je spojení a naše pravidlo pro zobrazování konjunkcí je adjunkce. Vzhledem k tomu, že použití tohoto pravidla může být naším nejlepším způsobem, jak ukázat (P^Q), můžeme se zaměřit na zobrazení P a poté zobrazit Q a poté provést adjunkci. Ale, samozřejmě máme velmi málo práce s-jen linka 1, což je negace. V takovém případě je obvykle moudré pokusit se o nepřímý důkaz. Začněte nepřímým důkazem P.,

nyní Musíme najít rozpor—žádný rozpor. Ale už je to zřejmé. Řádek 1 říká, že ani P, ani Q není pravda. Ale řádek 3 říká, že P je pravda. Tento rozpor musíme vyjádřit tím, že najdeme vzorec a jeho popření. Můžeme to udělat pomocí sčítání.

k dokončení důkazu použijeme tuto strategii znovu.

dokážeme, De morganovy teorémy jako problémy kapitole 9.,
Zde je obecné pravidlo pro to důkazy: Když se ukazuje jako podmíněné, vždy podmíněné odvození; jinak, zkuste přímé odvození; pokud se to nepodaří, pak zkuste nepřímé odvození.
8.4 problémy
- vyplňte následující důkazy. Každý bude vyžadovat nepřímou derivaci. Poslední dva jsou náročné.
- prokázat následující věty.
- (p^P).
- ((p→P)^(p→P)).
- (p→(p^Q)).
- ((P^Q)→(P→Q)).
- v běžné hovorové angličtině napište svůj vlastní platný argument s nejméně dvěma prostory., Váš argument by měl být jen odstavec (ne uspořádaný seznam vět nebo cokoli jiného, co vypadá jako formální logika). Přeložte ji do propoziční logiky a dokažte, že je platná pomocí nepřímé derivace.
Tento překlad názvu knihy Galileo se stal nejběžnějším, i když doslovnějším by byly matematické diskurzy a demonstrace. Překlady knihy zahrnují Drake (1974).