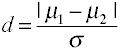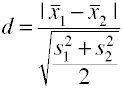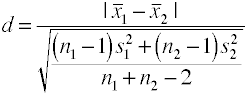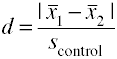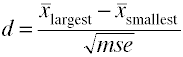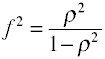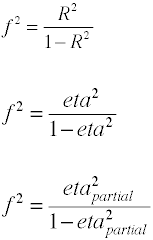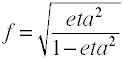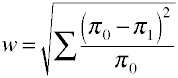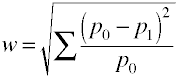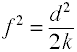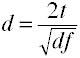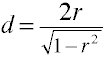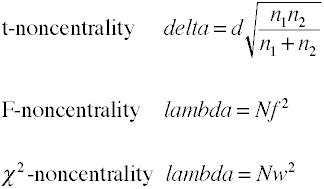en anvendelse af effektstørrelse er som et standardiseret indeks, der er uafhængigt af prøvestørrelse og kvantificerer størrelsen af forskellen mellem populationer eller forholdet mellem forklarende og responsvariabler. En anden anvendelse af effektstørrelse er dens anvendelse i udførelsestrømanalyse.
effektstørrelse for forskel i middel
effektstørrelse for forskelle i middel er angivet afcohens d er defineret med hensyn til populationsmidler (µs) og en populationsstandardafvigelse (σ) Som vist nedenfor.,
Der er flere forskellige måder, at man kunne estimere σ fra sample data whichleads til flere varianter i Cohen ‘ s d-familien.
ved at Bruge root mean square standard afvigelse
Anvendelse af den samlede standardafvigelse (Hedges g)
Denne version af Cohen ‘s d bruger de samlede standardafvigelse og er også kendt som Hække’ g.,
Du kan nemt opnå denne værdi fra en anova-program ved at tage kvadratroden af meansquare fejl, som er også kendt som root mean square error.
brug af kontrolgruppens standardafvigelse (glas’))
en anden version af Cohens d, der bruger standardafvigelsen for kontrolgruppen, kaldes også glas’..,
Mere end to grupper
Når der er mere end to grupper bruge forskellen mellem den største og smallestmeans divideret med kvadratroden af mean square error.
Effekt størrelse for F-nøgletal i regressionsanalyse
For OLS regression måling af effekter størrelse er F, som er defineret af Cohen som følger.,
igen, at der er flere måder, hvorpå effekten størrelsen kan beregnes fra sample data. Notethat η2 er et andet navn for R2.
Effekt størrelse for F-nøgletal i analysen af variansen
Den effekt, der anvendes i analyse af varians er defineret som forholdet mellem befolkning standarddeviations.,
selvom Cohens f er defineret som ovenfor, beregnes det sædvanligvis ved at tage kvadratroden af F2.
Effekt størrelse for χ2 fra contingency tabeller
vi endnu Engang starter med de definitoriske formel i form af befolkningens værdier.Effektstørrelse is er kvadratroden af den standardiserede chi-firkantede statistik.,
Og her er, hvor w er beregnet ved hjælp af sample data.
Her er en tabel over foreslåede værdier for lav, medium og høj effekt (Cohen, 1988). Disse værdier bør ikke tages som absolutter og bør fortolkes inden for rammerne af dit forskningsprogram. Værdierne for store effekter overskrides ofte i praksis med værdier Cohens d større end 1,0 ikke ualmindeligt.,Men ved hjælp af meget store effektstørrelser i potentiel effektanalyse er det nok ikke en god ide, somDet kan føre til under drevne undersøgelser.,formler
hvor k = antal grupper
Konverter t til d i to uafhængige grupper
Konverter r til at d for to uafhængige grupper
Noncentrality skøn
Power analyse ved hjælp af analytiske metoder, der kræver et skøn over noncentrality, som er basicallythe effekt størrelse ganget med en stikprøve faktor., Her er nogle formler til estimering af noncentralitet.
Eksempel power analyse
Her er et eksempel, der samler effekt størrelse og noncentrality i en magt-analyse.
overvej en envejsanalyse af varians med tre grupper (k = 3). Hvis vi forventer andeta2 til lige .,12 i hvilket tilfælde den effekt størrelse vil være
effect size f = sqrt(eta2/(1-eta2)) = sqrt(.12/(1-.12)) = .369
Med en forventet stikprøvestørrelse på 60 skøn noncentrality er
noncentrality coefficient lambda = N*f = 60*.369^2 = 60*.136 = 8.17
tællerens frihedsgrader er k-1 = 3-1 = 2, mens nævneren df er N-k = 60-3 = 57.Den kritiske værdi af F med 2 og 57 frihedsgrader er 3,16. Hvilket resulterer i en effekt på
power = noncentralFtail(df1,df2,lambda,Fcrit(2,57)) = noncentralFtail(2,57,8.17,3.16) = .703
således en n på 60 og effektstørrelse på .369 giver en forventet effekt på ca .7.
Vi kan forbedre effekten af .7 ved at anvende en projiceret stikprøvestørrelse på 75 i stedet for 60., Med samme effekt størrelse.369, får vi et nyt noncentralitet estimat af
noncentrality coefficient lambda = N*f = 75*.369^2 = 75*.136 = 10.2
tællergraderne af frihed forbliver de samme, mens nævneren df nu er lig med N-k = 75-3 = 72.Den kritiske værdi af F med 2 og 72 frihedsgrader på 3.12. Denne gang er strømmen
power = noncentralFtail(df1,df2,lambda,Fcrit(2,72)) = noncentralFtail(2,72,10.2,3.12) = .807
hvilket er inden for acceptable forskningsgrænser.
Bemærk, at forskellige stat pakker bruger forskellige navne og en anden rækkefølge af argumenter inthe funktion, som vi har kalder noncentralFtail. Du skal læse dokumentationen somkommer med din Soft .are.,
Becker, L. psykologi 590 kursus noter. Den ses 19 Jun 2009 <http://web.uccs.edu/lbecker/Psy590/es.htm>
Cohen, J. 1988. Statistisk effektanalyse for adfærdsvidenskaberne. Hillsdale, ne, Jersey:La ,rence Erlbaum Associates