Statistics Definitions > ANOVA
Contents:
- The ANOVA Test
- One Way ANOVA
- Zwei-Wege-ANOVA
- Was ist MANOVA?
- Was ist Factorial ANOVA?
- Wie führe ich einen ANOVA aus
- ANOVA vs. T Test
- Wiederholte Messungen ANOVA
- Sphärizität
Der ANOVA Test
Was ist ANOVA?, Sehen Sie sich das Video für eine Einführung, oder lesen Sie weiter unten:
immer Noch Probleme? Chegg.com wird Sie mit einem Tutor übereinstimmen (Ihre erste Lektion ist kostenlos!).
Ein ANOVA-Test ist ein Weg, um herauszufinden, ob Umfrage oder Experiment Ergebnisse signifikant sind. Mit anderen Worten, sie helfen Ihnen herauszufinden, ob Sie die Nullhypothese ablehnen oder die alternative Hypothese akzeptieren müssen.
Grundsätzlich testen Sie Gruppen, um festzustellen, ob es einen Unterschied zwischen ihnen gibt., Beispiele, wann Sie verschiedene Gruppen testen möchten:
- Eine Gruppe psychiatrischer Patienten versucht drei verschiedene Therapien: Beratung, Medikamente und Biofeedback. Sie wollen sehen, ob eine Therapie besser ist als die anderen.
- Ein Hersteller hat zwei verschiedene Verfahren, um Glühbirnen herzustellen. Sie wollen wissen, ob ein Prozess besser ist als der andere.
- Studenten verschiedener Hochschulen nehmen die gleiche Prüfung ab. Sie möchten sehen, ob ein College das andere übertrifft.
Was bedeutet“ Einweg „oder “ Zweiweg“?,
Einweg-oder Zweiweg bezieht sich auf die Anzahl unabhängiger Variablen (IVs) in Ihrer Varianzanalyse.
- One-way hat eine unabhängige variable (mit 2 Ebenen). Zum Beispiel: Marke von Getreide,
- Zwei-Wege hat zwei unabhängige Variablen (es kann mehrere Ebenen haben). Zum Beispiel: Marke von Getreide, Kalorien.
Was sind „Gruppen“ oder „Ebenen“?
Gruppen oder Ebenen sind verschiedene Gruppen innerhalb derselben unabhängigen Variablen. Im obigen Beispiel können Ihre Ebenen für „Marke von Getreide“ Glücksbringer, Rosinenkleie, Cornflakes sein-insgesamt drei Ebenen., Ihre Ebenen für“ Kalorien “ könnte sein: gesüßt, ungesüßt — insgesamt zwei Ebenen.
Nehmen wir an, Sie studieren, ob eine alkoholische Selbsthilfegruppe und individuelle Beratung kombiniert die effektivste Behandlung zur Senkung des Alkoholkonsums ist. Sie können die Studienteilnehmer in drei Gruppen oder Stufen aufteilen:
- Nur Medikamente,
- Medikamente und Beratung,
- nur Beratung.
Ihre abhängige Variable wäre die Anzahl der täglich konsumierten alkoholischen Getränke.,
Wenn Ihre Gruppen oder Ebenen eine hierarchische Struktur haben (jede Ebene hat eindeutige Untergruppen), verwenden Sie eine verschachtelte ANOVA für die Analyse.
Was bedeutet“ Replikation“?
Es ist, ob Sie Ihre Tests mit mehreren Gruppen replizieren (dh duplizieren). Mit einer Zwei-Wege-ANOVA mit Replikation haben Sie zwei Gruppen und Einzelpersonen innerhalb dieser Gruppe machen mehr als eine Sache (dh zwei Gruppen von Studenten von zwei Colleges, die zwei Tests machen). Wenn Sie nur eine Gruppe haben, die zwei Tests durchführt, würden Sie ohne Replikation verwenden.
Arten von Tests.,
Es gibt zwei Haupttypen: Einweg und Zweiweg. Zwei-Wege-tests können mit oder ohne Replikation.
- Einweg-ANOVA zwischen Gruppen: Wird verwendet, wenn Sie zwei Gruppen testen möchten, um festzustellen, ob ein Unterschied zwischen ihnen besteht.
- Zwei-Wege-ANOVA ohne Replikation: Wird verwendet, wenn Sie eine Gruppe haben und dieselbe Gruppe doppelt testen. Zum Beispiel testen Sie einen Satz von Personen, bevor und nachdem sie ein Medikament einnehmen, um zu sehen, ob es funktioniert oder nicht.
- Zwei-Wege-ANOVA mit Replikation: Zwei Gruppen, und die Mitglieder dieser Gruppen tun mehr als eine Sache., Zum Beispiel versuchen zwei Gruppen von Patienten aus verschiedenen Krankenhäusern zwei verschiedene Therapien.
Zurück nach oben
Einfache ANOVA
Eine einfache ANOVA wird verwendet, um zwei Mittel aus zwei unabhängigen (nicht verwandten) Gruppen unter Verwendung der F-Verteilung zu vergleichen. Die Nullhypothese für den Test ist, dass die beiden Mittel gleich sind. Daher bedeutet ein signifikantes Ergebnis, dass die beiden Mittel ungleich sind.
Beispiele für die Verwendung einer Einweg-ANOVA
Situation 1: Sie haben eine Gruppe von Personen, die zufällig in kleinere Gruppen aufgeteilt sind und verschiedene Aufgaben ausführen., Zum Beispiel könnten Sie die Auswirkungen von Tee auf die Gewichtsabnahme studieren und drei Gruppen bilden: grüner Tee, schwarzer Tee und kein Tee.
Situation 2: Ähnlich wie Situation 1, aber in diesem Fall werden die Individuen in Gruppen aufgeteilt, basierend auf einem Attribut, das sie besitzen. Zum Beispiel könnten Sie die Beinstärke von Menschen nach Gewicht studieren. Sie können die Teilnehmer in Gewichtskategorien (fettleibig, übergewichtig und normal) aufteilen und ihre Beinkraft an einer Gewichtsmaschine messen.,
Einschränkungen der Einweg-ANOVA
Eine Einweg-ANOVA teilt Ihnen mit, dass sich mindestens zwei Gruppen voneinander unterschieden haben. Aber es wird Ihnen nicht sagen, welche Gruppen unterschiedlich waren. Wenn Ihr Test eine signifikante f-Statistik zurückgibt, müssen Sie möglicherweise einen Ad-hoc-Test durchführen (z. B. den Test mit dem geringsten signifikanten Unterschied), um genau festzustellen, welche Gruppen einen Unterschied in den Mitteln hatten.
Back to Top
Zwei-Wege-ANOVA
Ein Zwei-Wege-ANOVA ist eine Erweiterung des One-Way ANOVA. Mit einer Möglichkeit haben Sie eine unabhängige Variable, die eine abhängige Variable beeinflusst., Mit einer Zwei-Wege-ANOVA gibt es zwei Unabhängige. Verwenden Sie eine Zwei-Wege-ANOVA, wenn Sie eine Messvariable (dh eine quantitative Variable) und zwei nominale Variablen haben. Mit anderen Worten, wenn Ihr Experiment ein quantitatives Ergebnis hat und Sie zwei kategorische erklärende Variablen haben, ist eine Zwei-Wege-ANOVA angemessen.
Zum Beispiel möchten Sie vielleicht herausfinden, ob bei Vorstellungsgesprächen eine Interaktion zwischen Einkommen und Geschlecht für die Angststufe besteht. Das Angstniveau ist das Ergebnis oder die Variable, die gemessen werden kann. Geschlecht und Einkommen sind die beiden kategorialen Variablen., Diese kategorialen Variablen sind auch die unabhängigen Variablen, die Faktoren in einer Zwei-Wege-ANOVA genannt werden.
Die Faktoren können in Ebenen aufgeteilt werden. Im obigen Beispiel könnte das Einkommensniveau in drei Ebenen aufgeteilt werden: niedriges, mittleres und hohes Einkommen. Das Geschlecht könnte in drei Ebenen unterteilt werden: männlich, weiblich und Transgender. Behandlungsgruppen sind alle möglichen Kombinationen der Faktoren. In diesem Beispiel gäbe es 3 x 3 = 9 Behandlungsgruppen.
Haupteffekt und Interaktionseffekt
Die Ergebnisse einer Zwei-Wege-ANOVA berechnen einen Haupteffekt und einen Interaktionseffekt., Der Haupteffekt ähnelt einer EINWEGANOVA: Der Effekt jedes Faktors wird separat betrachtet. Mit dem Interaktionseffekt werden alle Faktoren gleichzeitig berücksichtigt. Interaktionseffekte zwischen Faktoren sind einfacher zu testen, wenn in jeder Zelle mehr als eine Beobachtung vorhanden ist. Für das obige Beispiel könnten mehrere Stresswerte in Zellen eingegeben werden. Wenn Sie mehrere Beobachtungen in Zellen eingeben, muss die Anzahl in jeder Zelle gleich sein.
Zwei Nullhypothesen werden getestet, wenn Sie in jeder Zelle eine Beobachtung platzieren., Für dieses Beispiel wären diese Hypothesen:
H01: Alle Einkommensgruppen haben den gleichen mittleren Stress.
H02: Alle Geschlechtergruppen haben gleichen mittleren Stress.
Für mehrere Beobachtungen in Zellen würden Sie auch eine dritte Hypothese testen:
H03: Die Faktoren sind unabhängig oder der Interaktionseffekt existiert nicht.
Für jede Hypothese, die Sie testen, wird eine F-Statistik berechnet.
Annahmen für Zwei-Wege-ANOVA
- Die Population muss nahe an einer Normalverteilung liegen.
- Proben müssen unabhängig sein.
- Die Populationsvarianzen müssen gleich sein.,
- Gruppen müssen gleiche Stichprobengrößen haben.
Zurück nach oben
Was ist MANOVA?
MANOVA ist nur eine ANOVA mit mehreren abhängigen Variablen. Es ähnelt vielen anderen Tests und Experimenten, indem es herausfinden soll, ob die Antwortvariable (dh Ihre abhängige Variable) durch Manipulation der unabhängigen Variablen geändert wird. Der Test hilft, viele Forschungsfragen zu beantworten, darunter:
- Haben Änderungen an den unabhängigen Variablen statistisch signifikante Auswirkungen auf abhängige Variablen?
- Was sind die Wechselwirkungen zwischen abhängigen Variablen?,
- Was sind die Wechselwirkungen zwischen unabhängigen Variablen?
MANOVA Example
Angenommen, Sie wollten herausfinden, ob ein Unterschied in den Lehrbüchern die Punktzahlen der Schüler in Mathematik und Naturwissenschaften beeinflusst. Verbesserungen in Mathematik und Wissenschaft bedeuten, dass es zwei abhängige Variablen gibt, daher ist eine MANOVA angemessen.
Eine ANOVA gibt Ihnen einen einzelnen (univariaten) f-Wert, während eine MANOVA Ihnen einen multivariaten F-Wert gibt. MANOVA testet die mehreren abhängigen Variablen, indem neue, künstliche, abhängige Variablen erstellt werden, die Gruppenunterschiede maximieren., Diese neuen abhängigen Variablen sind lineare Kombinationen der gemessenen abhängigen Variablen.
Interpretation der MANOVA-Ergebnisse
Wenn der multivariate F-Wert angibt, dass der Test statistisch signifikant ist, bedeutet dies, dass etwas signifikant ist. Im obigen Beispiel würden Sie nicht wissen, ob sich die mathematischen Ergebnisse verbessert haben, die wissenschaftlichen Ergebnisse verbessert haben (oder beides)., Sobald Sie ein signifikantes Ergebnis haben, müssen Sie sich dann jede einzelne Komponente (die univariaten F-Tests) ansehen, um festzustellen, welche abhängigen Variablen zu dem statistisch signifikanten Ergebnis beigetragen haben.
Vor-und Nachteile von MANOVA vs. ANOVA
Vorteile
- Mit MANOVA können Sie mehrere abhängige Variablen testen.
- MANOVA kann vor Typ-I-Fehlern schützen.
- MANOVA ist um ein Vielfaches komplizierter als ANOVA, was es zu einer Herausforderung macht, zu sehen, welche unabhängigen Variablen abhängige Variablen beeinflussen.,
- Mit jeder neuen Variablen geht ein Freiheitsgrad verloren.
- Die abhängigen Variablen sollten so weit wie möglich unkorreliert sein. Wenn sie korreliert sind, bedeutet der Verlust der Freiheitsgrade, dass es nicht viele Vorteile gibt, mehr als eine abhängige Variable in den Test aufzunehmen.
Referenz:
(SFSU)
Zurück nach oben
Was ist Factorial ANOVA?
Eine faktorielle ANOVA ist eine Analyse des Varianztests mit mehr als einer unabhängigen Variablen oder „Faktor“. Es kann sich auch auf mehr als eine Ebene unabhängiger Variablen beziehen., Zum Beispiel hat ein Experiment mit einer Behandlungsgruppe und einer Kontrollgruppe einen Faktor (die Behandlung), aber zwei Ebenen (die Behandlung und die Kontrolle). Die Begriffe „Zwei-Wege“ und „Drei-Wege“ beziehen sich auf die Anzahl der Faktoren oder die Anzahl der Ebenen in Ihrem Test. Vier-Wege-ANOVA und höher werden selten verwendet, da die Testergebnisse komplex und schwer zu interpretieren sind.
- Eine bidirektionale ANOVA hat zwei Faktoren (unabhängige Variablen) und eine abhängige Variable. Zum Beispiel sind Zeit für das Studium und Vorkenntnisse Faktoren, die beeinflussen, wie gut Sie bei einem Test abschneiden.,
- Eine Drei-Wege-ANOVA hat drei Faktoren (unabhängige Variablen) und eine abhängige Variable. Zum Beispiel sind Studienzeit, Vorkenntnisse und Schlafstunden Faktoren, die beeinflussen, wie gut Sie einen Test durchführen
Factorial ANOVA ist eine effiziente Möglichkeit, einen Test durchzuführen. Anstatt eine Reihe von Experimenten durchzuführen, bei denen Sie eine unabhängige Variable gegen eine abhängige Variable testen, können Sie alle unabhängigen Variablen gleichzeitig testen.
Variabilität
In einer Einweg-ANOVA ist die Variabilität auf die Unterschiede zwischen Gruppen und die Unterschiede innerhalb von Gruppen zurückzuführen., In Factorial ANOVA werden jede Ebene und jeder Faktor miteinander gepaart („gekreuzt“). Dies hilft Ihnen zu sehen, welche Interaktionen zwischen den Ebenen und Faktoren. Wenn es eine Interaktion gibt, hängen die Unterschiede in einem Faktor von den Unterschieden in einem anderen ab.
Nehmen wir an, Sie führten eine Zwei-Wege-ANOVA durch, um die Leistung von Männern und Frauen bei einer Abschlussprüfung zu testen. Die Probanden hatten entweder 4, 6 oder 8 Stunden Schlaf.,
- IV1: SEX (männlich/weiblich)
- IV2: SLEEP (4/6/8)
- DV: Final Exam Score
Eine Zwei-Wege-faktorielle ANOVA würde Ihnen helfen, die folgenden Fragen zu beantworten:
- Ist Sex ein Haupteffekt? Mit anderen Worten, unterscheiden sich Männer und Frauen signifikant in ihrer Prüfungsleistung?
- Ist Schlaf ein Haupteffekt? Mit anderen Worten, unterscheiden sich Menschen, die 4,6 oder 8 Stunden Schlaf hatten, signifikant in ihrer Leistung?
- Gibt es eine signifikante Wechselwirkung zwischen Faktoren? Mit anderen Worten, wie interagieren Stunden Schlaf und Sex in Bezug auf die Prüfungsleistung?,
- Können Unterschiede in Geschlecht und Prüfungsleistung in den verschiedenen Schlafniveaus gefunden werden?
Annahmen der faktoriellen ANOVA
- Normalität: Die abhängige Variable ist normal verteilt.
- Unabhängigkeit: Beobachtungen und Gruppen sind unabhängig voneinander.
- Gleichheit der Varianz: Die Populationsvarianzen sind über Faktoren/Ebenen hinweg gleich.
So führen Sie eine ANOVA aus
Diese Tests sind sehr zeitaufwendig von Hand. In fast jedem Fall möchten Sie Software verwenden., In Excel stehen beispielsweise mehrere Optionen zur Verfügung:
- Zwei-Wege-ANOVA in Excel mit Replikation und ohne Replikation.
- One-way ANOVA in Excel 2013.
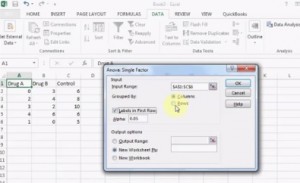
test in Excel.
ANOVA-Tests in Statistikpaketen werden auf parametrischen Daten ausgeführt. Wenn Sie Rank-oder geordnete Daten haben, möchten Sie eine nichtparametrische ANOVA ausführen (normalerweise unter einer anderen Überschrift in der Software, z. B. „nichtparametrische Tests“).,
Schritte
Es ist unwahrscheinlich, dass Sie diesen Test von Hand durchführen möchten, aber wenn Sie müssen, sind dies die Schritte, die Sie ausführen möchten:
- Finden Sie den Mittelwert für jede der Gruppen.
- Ermitteln Sie den Gesamtmittelwert (den Mittelwert der kombinierten Gruppen).
- Finde die innerhalb der Gruppe Variation; die Gesamtabweichung der Punktzahl jedes Mitglieds vom Gruppenmittelwert.
- Finden Sie die Variation zwischen den Gruppen: die Abweichung jedes Gruppenmittelwerts vom Gesamtmittelwert.
- Sie Finden die F-Statistik: das Verhältnis Zwischen der Gruppe Variation zu Variation Innerhalb der Gruppe.
ANOVA vs., T-Test
Der T-Test eines Schülers zeigt Ihnen an, ob es zwischen den Gruppen signifikante Unterschiede gibt. Ein t-Test vergleicht Mittel, während die ANOVA Varianzen zwischen Populationen vergleicht.
Sie könnten technisch eine Reihe von t-tests auf Ihre Daten. Wenn die Anzahl der Gruppen jedoch zunimmt, erhalten Sie möglicherweise viele Paarvergleiche, die Sie ausführen müssen. ANOVA gibt Ihnen eine einzelne Zahl (die f-Statistik) und einen p-Wert, um die Nullhypothese zu unterstützen oder abzulehnen.,
Zurück nach oben
Wiederholte Messungen ANOVA
Eine wiederholte Messungen ANOVA ist fast die gleiche wie Einweg-ANOVA,mit einem Hauptunterschied: Sie testen verwandte Gruppen, nicht unabhängige. Es wird als wiederholte Messungen bezeichnet, da dieselbe Gruppe von Teilnehmern immer wieder gemessen wird. Zum Beispiel könnten Sie den Cholesterinspiegel derselben Patientengruppe nach 1, 3 und 6 Monaten nach Ernährungsumstellung untersuchen. In diesem Beispiel ist die unabhängige Variable “ Zeit „und die abhängige Variable“ Cholesterin.,“Die unabhängige Variable wird normalerweise als Innerhalb-Subjekte-Faktor bezeichnet.
Wiederholte Messungen ANOVA ähnelt einem einfachen multivariaten Design. In beiden Tests werden immer wieder dieselben Teilnehmer gemessen. Bei wiederholten Messungen wird jedoch dasselbe Merkmal mit einem anderen Zustand gemessen. Zum Beispiel wird der Blutdruck über die Bedingung „Zeit“gemessen. Für einfaches multivariates Design ändert sich die Eigenschaft. Zum Beispiel könnten Sie Blutdruck, Herzfrequenz und Atemfrequenz im Laufe der Zeit messen.,
Gründe für die Verwendung wiederholter Messungen ANOVA
- Wenn Sie Daten von denselben Teilnehmern über einen bestimmten Zeitraum sammeln, werden individuelle Unterschiede (eine Quelle für Gruppenunterschiede) reduziert oder beseitigt.
- Das Testen ist leistungsfähiger, da die Stichprobengröße nicht zwischen Gruppen aufgeteilt ist.
- Der Test kann wirtschaftlich sein, da Sie dieselben Teilnehmer verwenden.,
Annahmen für wiederholte Messungen ANOVA
Die Ergebnisse Ihrer wiederholten Messungen ANOVA sind nur gültig, wenn die folgenden Annahmen nicht verletzt wurden:
- Es muss eine unabhängige Variable und eine abhängige Variable geben.
- Die abhängige Variable muss eine kontinuierliche Variable auf einer Intervallskala oder einer Verhältnisskala sein.
- Die unabhängige Variable muss kategorisch sein, entweder auf der nominalen Skala oder auf der Ordinalskala.
- Idealerweise ist die Abhängigkeit zwischen Gruppenpaaren gleich („Sphärizität“)., Korrekturen sind möglich, wenn diese Annahme verletzt wird.
Wiederholte Messungen ANOVA in SPSS: Schritte
Schritt 1: Klicken Sie auf „Analysieren“ und fahren Sie dann mit der Maus über „Allgemeines lineares Modell“.“Klicken“ Wiederholte Maßnahmen.“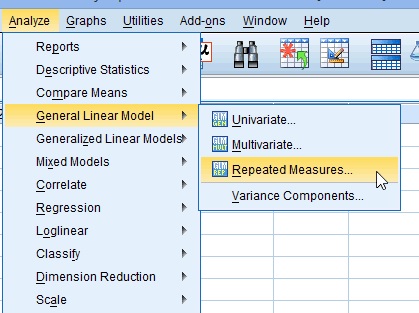
Schritt 2: Ersetzen Sie den Namen“ factor1 “ durch etwas, das Ihre unabhängige Variable darstellt. Zum Beispiel könnten Sie „Alter“ oder „Zeit“ setzen.“
Schritt 3: Geben Sie die „Anzahl der Ebenen.“So oft wurde die abhängige Variable gemessen. Wenn Sie beispielsweise jede Woche für insgesamt 4 Wochen Messungen durchführen, beträgt diese Zahl 4.,
Schritt 4: Klicken Sie auf die Schaltfläche „Hinzufügen“ und geben Sie Ihrer abhängigen Variablen einen Namen.
Schritt 5: Klicken Sie auf die Schaltfläche „Hinzufügen“. Ein Feld zum Definieren wiederholter Maßnahmen wird angezeigt. Klicken Sie auf die Schaltfläche“ Definieren“.
Schritt 6: Bewegen Sie Ihre Variablen mit den Pfeiltasten von links nach rechts, sodass Ihr Bildschirm dem folgenden Bild ähnelt: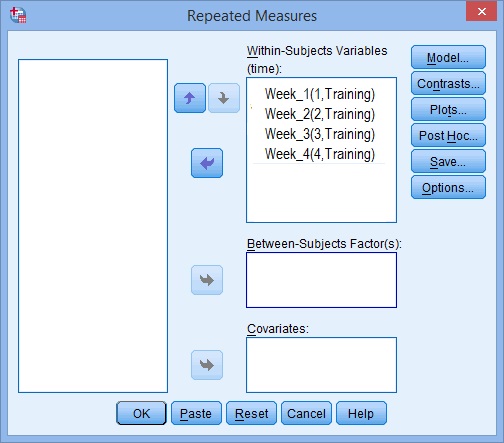
Schritt 7: Klicken Sie auf“ Plots “ und übertragen Sie den Faktor mit den Pfeiltasten aus dem linken Feld auf das Feld Horizontale Achse.
Schritt 8: Klicken Sie auf “ Hinzufügen „und dann auf“ Weiter “ am unteren Rand des Fensters.,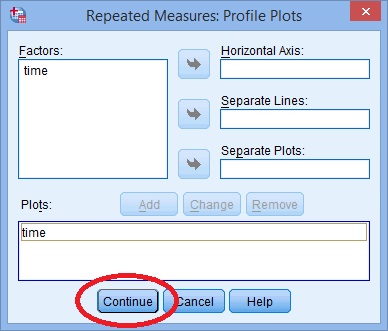
Schritt 9: Klicken sie auf“ Optionen“, dann übertragen sie ihre faktoren von der linken box zu die Display Bedeutet für box auf der rechten seite.
Schritt 10: Klicken Sie auf die folgenden Kontrollkästchen:
- Haupteffekte vergleichen.
- Beschreibende Statistiken.
- Schätzungen der effektgröße.
Schritt 11: Wählen Sie „Bonferroni“ aus dem Dropdown-Menü unter Konfidenzintervall Anpassung.
Schritt 12: Klicken Sie auf „Weiter“ und dann auf „OK“, um den Test auszuführen.,
Zurück nach oben
Sphärizität
In der Statistik bezieht sich Sphärizität (ε) auf Mauchlys Sphärizitätstest, der 1940 von John W. Mauchly entwickelt wurde, der den ersten elektronischen Allzweck-Computer mitentwickelte.
Definition
Sphärizität wird als Annahme bei wiederholten Messungen ANOVA verwendet. Die Annahme besagt, dass die Varianzen der Unterschiede zwischen allen möglichen Gruppenpaaren gleich sind. Wenn Ihre Daten gegen diese Annahme verstoßen, kann dies zu einem Anstieg eines Fehlers vom Typ I führen (die falsche Ablehnung der Nullhypothese).,
Es ist sehr häufig, dass wiederholte Maßnahmen ANOVA zu einer Verletzung der Annahme führen. Wenn die Annahme verletzt wurde, wurden Korrekturen entwickelt, die eine Erhöhung der Fehlerrate vom Typ I vermeiden können. Die Korrektur wird auf die Freiheitsgrade in der F-Verteilung angewendet.
Mauchlys Sphärizitätstest
Mauchlys Test auf Sphärizität kann in der Mehrzahl der statistischen Software ausgeführt werden, wo er tendenziell der Standardtest für Sphärizität ist. Mauchly-test ist ideal für mittelgroße Proben., Es kann Sphärizität in kleinen Proben nicht erkennen und es kann in großen Proben übermäßig erkennen.
Wenn der Test einen kleinen p-Wert (p) zurückgibt.05), dies ist ein Hinweis darauf, dass Ihre Daten gegen die Annahme verstoßen haben. Das folgende Bild der SPSS-Ausgabe für ANOVA zeigt, dass die Bedeutung „sig“, die Mauchlys beigemessen wird, ist .274. Dies bedeutet, dass die Annahme für diesen Datensatz nicht verletzt wurde.
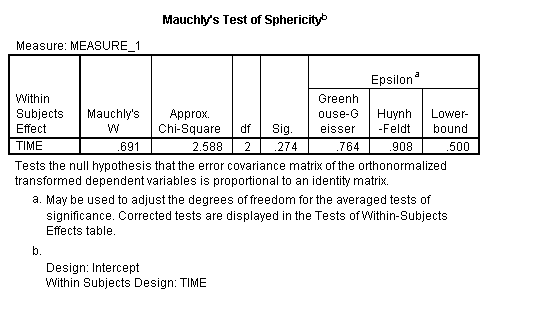
Bild: UVM.,EDU
Sie würden das obige Ergebnis als „Mauchlys Test zeigte an, dass die Annahme der Sphärizität nicht verletzt worden war, χ2(2) = 2.588, p = .274.“
Wenn Ihr Test einen kleinen p-Wert zurückgegeben hat, sollten Sie eine Korrektur anwenden, normalerweise entweder die:
- Greehouse-Geisser-Korrektur.
- Huynh-Feldt-Korrektur.
Wenn ε ≤ 0,75 (oder Sie wissen nicht, was der Wert für die Statistik ist), verwenden Sie die Li-Geisser-Korrektur.
Bei Verwendung von > .75, verwenden sie die Huynh-Feldt korrektur.,
Zurück nach oben
Grand mean
ANOVA vs Regression
——————————————————————————
Benötigen Sie Hilfe bei Hausaufgaben oder Testfragen? Mit Chegg Study erhalten Sie Schritt-für-Schritt-Lösungen für Ihre Fragen von einem Experten auf diesem Gebiet. Ihre ersten 30 Minuten mit einem Chegg Tutor ist kostenlos!