A Regression Model for Survival Data
ich zuvor schrieb darüber, wie die Berechnung des Kaplan–Meier-Kurve für das überleben der Daten. Als nichtparametrischer Schätzer bietet er einen guten Überblick über die Überlebenskurve eines Datensatzes. Was Sie jedoch nicht tun können, ist die Modellierung der Auswirkungen von Kovariaten auf das Überleben. In diesem Artikel konzentrieren wir uns auf das Cox Proportional Hazards Model, eines der am häufigsten verwendeten Modelle für Überlebensdaten.
Wir werden in einige Tiefe gehen, wie die Schätzungen zu berechnen., Dies ist wertvoll, da wir sehen werden, dass die Schätzungen nur von der Reihenfolge der Fehler und nicht von ihren tatsächlichen Zeiten abhängen. Wir werden auch kurz einige knifflige Fragen zur Kausalinferenz diskutieren, die speziell für die Überlebensanalyse sind.
Wir denken normalerweise über Überlebensdaten in Bezug auf Überlebenskurven wie die folgenden nach.,
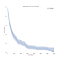
Auf der x-Achse haben wir die Zeit in Tagen. Auf der y-Achse haben wir (einen Schätzer für) den Prozentsatz (technisch gesehen, Anteil) der Probanden in der Bevölkerung, die zu dieser Zeit „überleben“. Überleben kann figurativ oder wörtlich sein., Es könnte sein, ob Menschen bis zu einem bestimmten Alter leben, ob eine Maschine eine bestimmte Zeit ohne Unterbrechung aushält, oder ob jemand nach dem Verlust seines Arbeitsplatzes eine bestimmte Zeit arbeitslos bleibt.
Entscheidend ist, dass die Komplikation in der Überlebensanalyse darin besteht, dass einige Probanden ihren „Tod“ nicht beobachtet haben. Sie sind möglicherweise noch am Leben, eine Maschine funktioniert möglicherweise noch oder jemand ist zum Zeitpunkt der Datenerfassung noch arbeitslos., Solche Beobachtungen werden als „richtig zensiert“ bezeichnet und der Umgang mit Zensur bedeutet, dass die Überlebensanalyse unterschiedliche statistische Werkzeuge erfordert.
Wir bezeichnen die überlebende Funktion als S, eine Funktion der Zeit. Seine Ausgabe ist der Prozentsatz der Probanden, die zum Zeitpunkt t überleben. (Auch hier ist es technisch gesehen ein Verhältnis zwischen 0 und 1, aber ich werde die beiden Wörter austauschbar verwenden). Der Einfachheit halber werden wir die technische Annahme machen, dass, wenn wir lange genug warten, alle Fächer „sterben“ werden.“
Wir indizieren die Subjekte mit einem Index wie i oder j., Die Ausfallzeiten der gesamten Population werden mit einem ähnlichen Index für die Zeitvariable t angegeben.

Eine weitere zu berücksichtigende Feinheit ist, ob wir die Zeit als diskret (z. B. Woche für Woche) oder kontinuierlich behandeln. Philosophisch gesehen messen wir die Zeit immer nur in diskreten Schritten (z. B. bis zur nächsten Sekunde)., In der Regel sagen uns unsere Daten nur, ob jemand in einem bestimmten Jahr gestorben ist oder ob eine Maschine an einem bestimmten Tag ausgefallen ist. Ich werde zwischen den diskreten und kontinuierlichen Fällen hin und her gehen, um die Ausstellung so klar wie möglich zu halten.
Wenn wir versuchen, die Auswirkungen von Kovariaten (z. B. Alter, Geschlecht, Rasse, Maschinenhersteller) zu modellieren, sind wir normalerweise daran interessiert, die Auswirkungen der Kovariate auf die Gefahrenrate zu verstehen. Die Gefahrenrate ist die momentane Wahrscheinlichkeit eines Versagens / Todes/Zustandsübergangs zu einem bestimmten Zeitpunkt t, abhängig davon, dass sie bereits so lange überlebt hat., Wir werden es λ(t) bezeichnen. Zeit als diskret behandeln:
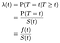
Wobei f die Gesamtwahrscheinlichkeitsdichte des Versagens zum Zeitpunkt t. Wir können die diskreten und kontinuierlichen Fälle vereinheitlichen, indem wir Delta-Funktionen in der Wahrscheinlichkeitsdichte „Funktion“zulassen. Somit ist das Ergebnis λ = f / S für den kontinuierlichen Fall gleich.
Lassen Sie uns ein Beispiel beheben., Betrachten wir den Kontext einer klinischen Studie, in der ein Medikament zunächst dazu führt, dass eine Krankheit in Remission geht. Wir werden sagen, dass das Medikament für ein Subjekt „versagt“, wenn die Krankheit für ein Subjekt fortschreitet. Angenommen, der Krankheitsstatus der Probanden wird jede Woche gemessen. Wenn λ(3) = 0,1 ist, bedeutet dies, dass eine Wahrscheinlichkeit von 10% besteht, dass für ein bestimmtes Subjekt, wenn sie sich noch vor Woche 3 in Remission befinden, ihre Krankheit in Woche 3 fortschreitet. Die anderen 90% bleiben in Remission.,
Als nächstes ist die Gesamtwahrscheinlichkeitsdichtefunktion f nur die Ableitung von S in Bezug auf die Zeit. (Wiederum, wenn die Zeit diskret ist, ist f nur die Summe einiger Delta-Funktionen).,341fa8b2″>
Dies bedeutet, dass wir, wenn wir die Gefahrenfunktion kennen, diese Differentialgleichung für S lösen können:
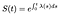
Wenn die Zeit diskret ist, wird das Integral einer Summe von Delta-Funktionen zu jeder diskreten Zeit zu einer Summe der Gefahren.,
Okay, das fasst die Notation und Grundbegriffe zusammen, die wir brauchen werden. Lasst uns weiter über Modelle diskutieren.
Nicht -, halb-und vollparametrische Modelle
Wie bereits erwähnt, sind wir typischerweise an der Modellierung der Gefährdungsrate λ interessiert.
In einem nichtparametrischen Modell machen wir keine Annahmen über die funktionelle Form von λ. Die Kaplan-Meier-Kurve ist in diesem Fall der maximale Wahrscheinlichkeitsschätzer. Der Nachteil ist, dass es dadurch schwierig ist, Effekte von Kovariaten zu modellieren. Es ist ein bisschen wie die Verwendung eines Streudiagramms, um die Wirkung einer Kovariate zu verstehen., Nicht unbedingt so hilfreich wie ein vollständig parametrisches Modell wie eine lineare Regression.
In einem vollständig parametrischen Modell machen wir eine Annahme für die genaue funktionelle Form von λ. Eine Diskussion der vollständig parametrischen Modelle ist ein vollständiger Artikel für sich, aber es lohnt sich eine sehr kurze Diskussion. Die folgende Tabelle zeigt drei der gängigsten vollparametrischen Modelle. Jeder wird durch den nächsten verallgemeinert und geht von 1 zu 2 zu 3 Parametern. Die Funktionsform für die Gefahrenfunktion ist in der mittleren Spalte dargestellt. Der Logarithmus der Gefahrenfunktion wird ebenfalls in der letzten Spalte angezeigt., Es wird angenommen, dass alle Parameter (ɣ, α, μ) positiv sind, außer dass μ in der generalisierten Weibull-Verteilung (Reproduzieren der Weibull-Verteilung) 0 sein könnte.

Ein Blick auf den Logarithmus zeigt uns, dass das Exponentialmodell davon ausgeht, die Funktion ist konstant. Das Weibull-Modell geht davon aus, dass dies zunimmt, wenn α>1, konstant, wenn α=1 und abnehmend, wenn α<1., Das generalisierte Weibull-Modell beginnt genauso wie das Weibull-Modell (am Anfang ln S = 0). Danach beginnt eine zusätzliche Amtszeit.
Das Problem bei diesen Modellen besteht darin, dass sie starke Annahmen über die Daten treffen. In bestimmten Kontexten kann es Gründe geben zu glauben, dass diese Modelle gut passen. Mit diesen und mehreren anderen verfügbaren Optionen besteht jedoch ein hohes Risiko, aufgrund von Fehlentscheidungen des Modells falsche Schlussfolgerungen zu ziehen.
Aus diesem Grund ist das Cox-Proportionalmodell, ein halbparametrisches Modell, so beliebt., Es werden keine funktionalen Annahmen über die Form der Gefahrenfunktion gemacht; stattdessen werden funktionale Annahmen über die Auswirkungen der Kovariaten allein gemacht.,
Das Cox Proportional Hazards Model
Das Cox Proportional Hazards Model wird üblicherweise in Bezug auf die Zeit t, den kovariaten Vektor x und den Koeffizientenvektor β als
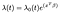
wobei λₒ eine beliebige Funktion der Zeit ist, die baseline hazards. Das Punktprodukt von X und β wird im Exponenten genau wie in der linearen Standardregression genommen., Unabhängig von den Kovariaten der Werte haben alle Probanden die gleiche Ausgangsgefahr λₒ. Danach werden Anpassungen basierend auf den Kovariaten vorgenommen.
Interpretation der Ergebnisse
Angenommen, wir haben für die Minute ein Cox Proportional Hazards model an unsere Daten angepasst, das aus
- Einer Spalte bestand, die die Zeit für jedes Subjekt angibt
- Eine Spalte, die angibt, ob das Subjekt „beobachtet“ wurde (um versagt zu haben, oder in unserem bevorzugten Beispiel, um ihren Krankheitsfortschritt zu haben). Ein Wert von 1 bedeutet, dass das Subjekt seinen Krankheitsfortschritt hatte., Ein Wert von 0 bedeutet, dass die Krankheit zum letzten Beobachtungszeitpunkt nicht fortgeschritten war. Die Beobachtung wurde zensiert.
- Spalten für unsere Kovariaten X.
Nach der Anpassung erhalten wir Werte für β. Angenommen, der Einfachheit halber gibt es eine einzelne Kovariate. Ein Wert von β=0,1 bedeutet, dass eine Erhöhung der Kovariate um einen Betrag von 1 zu einer etwa 10% igen Wahrscheinlichkeit des Fortschreitens der Krankheit zu einem bestimmten Zeitpunkt führt., Der genaue Wert ist in der Tat

Für kleine Werte von β ist der Wert von β selbst eine ziemlich gute Annäherung an den genauen Anstieg der Gefahr. Für größere Werte von β muss der genaue Betrag berechnet werden.
Eine andere Möglichkeit, β=0,1 auszudrücken, besteht darin, dass mit zunehmendem x die Gefahr um 10% pro Anstieg von x um 1 zunimmt. Die größere, 10.,52% entstehen durch (kontinuierliche) Compoundierung, genau wie bei Zinseszinsen.
Außerdem bedeutet β=0 keinen Effekt und β negativ bedeutet, dass mit zunehmender Kovariate ein geringeres Risiko besteht. Beachten Sie, dass es im Gegensatz zu Standardregressionen keinen Abfangbegriff gibt. Stattdessen wird das Intercept in die Baseline Hazard λₒ absorbiert, die ebenfalls geschätzt werden kann (siehe unten).
Unter der Annahme, dass wir die Baseline Hazard-Funktion geschätzt haben, können wir die Survivor-Funktion erstellen.,
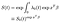
Die Baseline-Funktion wird auf die Potenz des exp-Faktors(xßß) erhöht, der aus den Kovariaten. Bei der Interpretation der Baseline-Survivor-Funktion, die in etwa die Rolle des Intercept-Terms in einer regelmäßigen linearen Regression spielt, sollte etwas Vorsicht walten gelassen werden. Wenn die Kovariaten zentriert wurden (Mittelwert 0), stellt sie die Überlebensfunktion für das „durchschnittliche“ Subjekt dar.,
Schätzung des Cox Proportional Hazards Model
In den 1970er Jahren schlug David Cox, ein britischer Mathematiker, einen Weg vor, β zu schätzen, ohne die Grundgefahr λₒ schätzen zu müssen. Auch hier kann die Ausgangsgefahr danach abgeschätzt werden. Wie bereits erwähnt, werden wir sehen, dass es auf die Reihenfolge der beobachteten Fehler ankommt, nicht auf die Zeiten selbst.
Vor dem Sprung in die Schätzung lohnt es sich, Krawatten zu diskutieren. Da wir normalerweise nur Daten in diskreten Schritten beobachten, können zwei Fehler gleichzeitig auftreten., Beispielsweise können zwei Maschinen in derselben Woche ausfallen und die Aufzeichnung erfolgt nur wöchentlich. Diese Verbindungen machen die Analyse der Situation ziemlich kompliziert, ohne viel Einblick hinzuzufügen. Folglich werde ich die Schätzungen im Falle von no ties ableiten.
Erinnern Sie sich daran, dass unsere Daten aus Beobachtungen einiger Zahlenfehler zu diesem Zeitpunkt bestehen. Lassen Sie R (t) die Population „gefährdet“ zum Zeitpunkt t bezeichnen. Wenn ein Subjekt in unserer Studie versagt hat (z. B. Krankheit fortgeschritten), bevor Zeit t, sind sie nicht „gefährdet“.,“Wenn ein Subjekt in unserer Studie seine Beobachtung zu einem Zeitpunkt vor time t zensiert hat, sind sie auch nicht „gefährdet“.“
Auf die übliche Weise möchten wir eine Likelihood-Funktion erstellen (wie hoch ist die Wahrscheinlichkeit, dass wir die Daten, die wir gemacht haben, angesichts der Kovariaten und Koeffizienten beobachtet hätten) und diese dann optimieren, um einen Maximum-Likelihood-Schätzer zu erhalten.
Für jedes diskrete Mal, wenn wir einen Fehler von Subjekt j beobachteten, ist die Wahrscheinlichkeit, dass dies auftritt, da ein Fehler aufgetreten ist, geringer. Die Summe wird über alle gefährdeten Personen zum Zeitpunkt j übernommen.,

Beachten Sie, dass die Ausgangsgefahr λₒ ausgefallen ist! Sehr bequem. Aus diesem Grund ist die Wahrscheinlichkeit, die wir konstruieren, nur eine teilweise Wahrscheinlichkeit. Beachten Sie auch, dass die Zeiten überhaupt nicht angezeigt werden., Der Begriff für Subjekt j hängt nur davon ab, welche Subjekte zum Zeitpunkt j noch am Leben sind, was wiederum nur von der Reihenfolge abhängt, in der die Subjekte zensiert oder beobachtet werden, um zu scheitern.
Die partielle Wahrscheinlichkeit ist natürlich nur das Produkt dieser Begriffe, eine für jeden Fehler, den wir beobachten (keine Begriffe für zensierte Beobachtungen).,
Die Log-Teilwahrscheinlichkeit ist dann
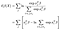
Die Anpassung erfolgt mit numerischen Standardmethoden, beispielsweise im Python-Paket statsmodels und die Varianz-Kovarianz-Matrix für die Schätzungen wird durch die (Inverse der) Fisher-Informationsmatrix angegeben. Nichts Aufregendes hier.,
Schätzung der Überlebensgrundfunktion
Nachdem wir die Koeffizienten geschätzt haben, können wir die Überlebensfunktion schätzen. Dies ist der Schätzung einer Kaplan-Meier-Kurve sehr ähnlich.
Wir postulieren Begriffe α indiziert durch i. Zum Zeitpunkt i sollte die Überlebenskurve der Basislinie um einen Bruchteil α abnehmen, der den Anteil der gefährdeten Personen darstellt, die zum Zeitpunkt i versagen., Mit anderen Worten
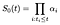
Um den maximalen Wahrscheinlichkeitsschätzer für α zu berechnen, betrachten wir den Wahrscheinlichkeitsbeitrag von Subjekt i, der fehlschlägt zum Zeitpunkt i und getrennt den Beitrag von denen, die zum Zeitpunkt i zensiert werden i.
Für ein Subjekt, das zum Zeitpunkt i versagt, ist die Wahrscheinlichkeit durch die Wahrscheinlichkeit gegeben, dass sie zum Zeitpunkt i am Leben sind, abzüglich der Wahrscheinlichkeit, dass sie zum nächsten Mal leben i+1. (Wir gehen vorübergehend davon aus, dass die Zeiten bestellt sind).,
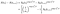
Wenn sie stattdessen zum Zeitpunkt i zensiert werden, ist der Beitrag nur die Wahrscheinlichkeit, dass sie zum Zeitpunkt nach i am Leben sind, dh dass sie noch nicht gestorben sind., Dies ist nur
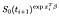
Es gibt einen extra Begriff aus den Themen, beobachtet wurden (D. H. beobachtet, um zu scheitern, anstatt zensiert)., Die Log Wahrscheinlichkeit wird
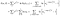
Ich war ein bisschen schlampig, Endpunkte zu verfolgen (i vs. i+1), aber es wird alles klappen.
Es gibt nur α-Begriffe für Probanden, bei denen wir beobachtet haben, dass sie fehlschlagen., Wenn wir in Bezug auf α-j unterscheiden und keine Bindungen annehmen, erhalten wir einen Beitrag aus der Summe links nur für zum Zeitpunkt j lebende Subjekte und einen einzigen Beitrag aus dem Begriff rechts.,qual auf 0 bedeutet, dass wir die Schätzungen der maximalen Wahrscheinlichkeit für α erhalten können, indem wir unsere Schätzungen für β als Lösung für die verschiedenen Gleichungen verwenden, eine für jedes Subjekt, bei dem beobachtet wurde, dass es fehlschlägt:
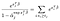
Erweiterungen und Vorbehalte
Über Cox Proportional Hazards-Modelle gibt es noch viel mehr zu sagen, aber ich werde versuchen, die Dinge kurz zu halten und nur ein paar Dinge zu erwähnen.,
Zum Beispiel möchte man zeitvariierende Regressoren in Betracht ziehen, und dies ist möglich.
Die andere entscheidende Sache zu beachten ist weggelassen variable Bias. In der linearen Standardregression sind ausgelassene Variablen, die nicht mit den Regressoren korreliert sind, kein großes Problem. Dies trifft in der Überlebensanalyse nicht zu. Angenommen, wir haben zwei gleich große und abgetastete Unterpopulationen in unseren Daten mit jeweils einer konstanten Gefahrenrate, eine ist 0,1 und die andere ist 0,5. Zunächst werden wir eine hohe Gefährdungsrate sehen (im Durchschnitt nur 0,3)., Im Laufe der Zeit wird die Bevölkerung mit einer hohen Gefährdungsrate die Bevölkerung verlassen, und wir werden eine Gefährdungsrate beobachten, die in Richtung 0.1 abnimmt. Wenn wir die Variable weglassen, die diese beiden Populationen darstellt, wird unsere Grundrisikorate durcheinander gebracht.