8.1 Ein historisches Beispiel
In seinem Buch, Die Beiden Neuen Wissenschaften, Galileo, Galilea (1564-1642) gibt mehrere Argumente, die gedacht, um zu demonstrieren, dass es keine solche Sache wie die tatsächlichen unendlichen oder tatsächlichen infinitesimals. Eines seiner Argumente kann auf folgende Weise rekonstruiert werden. Galileo schlägt vor, dass wir davon ausgehen, dass es eine tatsächliche Unendlichkeit natürlicher Zahlen gibt (die natürlichen Zahlen sind die positiven ganzen Zahlen ab 1):
{1, 2, 3, 4, 5, 6, 7, ….,}
Er schlägt auch vor, dass wir davon ausgehen, dass es eine tatsächliche Unendlichkeit der Quadrate der natürlichen Zahlen gibt.
{1, 4, 9, 16, 25, 36, 49, ….}
Beachten Sie aus Galileo-Gründen, dass diese beiden Gruppen (heute würden wir sie „sets“ nennen) die gleiche Größe haben. Wir können dies sehen, weil wir sehen können, dass es eine Eins-zu-Eins-Korrespondenz zwischen den beiden Gruppen gibt.,
| {1, | 2, | 3, | 4, | 5, | 6, | 7, ….,div> | |
| {1, | 4, | 9, | 16, | 25, | 36, | 49, …} |
Wenn wir jede natürliche Zahl mit einer und nur einer quadratischen Zahl verknüpfen können und wenn wir jede quadratische Zahl mit einer und nur einer natürlichen Zahl verknüpfen können, müssen diese Sätze dieselbe Größe haben.,
Aber warte einen Moment, sagt Galileo. Es gibt offensichtlich sehr viel mehr natürliche Zahlen als quadratische Zahlen. Das heißt, jede quadratische Zahl ist in der Liste der natürlichen Zahlen, aber viele der natürlichen Zahlen sind nicht in der Liste der Quadratzahlen. Die folgenden Zahlen sind alle in der Liste der natürlichen Zahlen, aber nicht in der Liste der Quadratzahlen.
{2, 3, 5, 6, 7, 8, 10, ….,}
Also, Galileo Gründe, wenn es viele Zahlen in der Gruppe der natürlichen Zahlen, die nicht in der Gruppe der Quadratzahlen sind, und wenn es keine Zahlen in der Gruppe der Quadratzahlen, die nicht in den natürlichen Zahlen sind, dann sind die natürlichen Zahlen größer als die Quadratzahlen. Und wenn die Gruppe der natürlichen Zahlen größer ist als die Gruppe der Quadratzahlen, dann sind die natürlichen Zahlen und die Quadratzahlen nicht gleich groß.,
Wir haben zwei Schlussfolgerungen gezogen: Die Menge der natürlichen Zahlen und die Menge der Quadratzahlen sind gleich groß; und die Menge der natürlichen Zahlen und die Menge der Quadratzahlen sind nicht gleich groß. Das ist widersprüchlich.
Galileo argumentiert, dass der Grund, warum wir einen Widerspruch erreicht haben, darin besteht, dass wir angenommen haben, dass es tatsächliche Unendlichkeiten gibt. Er kommt daher zu dem Schluss, dass es keine tatsächlichen Unendlichkeiten gibt.
8.2 Indirekte Beweise
Unsere Logik ist noch nicht stark genug, um einige gültige Argumente zu beweisen. Betrachten Sie das folgende Argument als Beispiel.,
(P→(QvR))
Q
R
P
Dieses argument sieht gültig. Unter der ersten Prämisse wissen wir: Wenn P wahr wäre, dann wäre (Q v R) wahr. Aber dann wären entweder Q oder R oder beides wahr. Und durch die zweite und dritte Prämisse wissen wir: Q ist falsch und R ist falsch. Es kann also nicht sein, dass (Q v R) wahr ist, und es kann also nicht sein, dass P wahr ist.
Wir können das Argument mit einer Wahrheitstabelle überprüfen. Unser Tisch wird komplex sein, weil einer unserer Prämissen komplex ist.,
In any kind of situation in which all the premises are true, the conclusion is true., Das heißt: Die Prämissen sind alle nur in der letzten Reihe wahr. Für diese Zeile gilt auch die Schlussfolgerung. Dies ist also ein gültiges Argument.
Aber nehmen Sie sich eine Minute Zeit und versuchen Sie, dieses Argument zu beweisen. Wir beginnen mit

Und jetzt sind wir stehengeblieben. Wir können keine unserer Regeln anwenden. Hier ist ein gültiges Argument, dass wir unser Argumentationssystem nicht stark genug gemacht haben, um es zu beweisen.
Es gibt mehrere Möglichkeiten, dieses Problem zu beheben und unser Denksystem stark genug zu machen., Eine der ältesten Lösungen ist die Einführung einer neuen Beweismethode, die traditionell als „reductio ad absurdum“ bezeichnet wird und eine Reduktion auf Absurdität bedeutet. Diese Methode wird auch oft als „indirekter Beweis“ oder „indirekte Ableitung“bezeichnet.
Die Idee ist, dass wir die Ablehnung unserer Schlussfolgerung annehmen und dann zeigen, dass ein Widerspruch entsteht. Ein Widerspruch wird gezeigt, wenn wir einen Satz Ψ und seine Negation prove beweisen. Dies kann jeder Satz sein. Der Punkt ist, dass wir angesichts des Prinzips der Bivalenz etwas Falsches bewiesen haben müssen. Denn wenn Ψ wahr ist, dann ist Ψ falsch; und wenn Ψ wahr ist, dann ist Ψ falsch., Wir müssen nicht wissen, was falsch ist (Ψ oder Ψ); es genügt zu wissen, dass einer von ihnen sein muss.
Denken Sie daran, dass wir unser logisches System so aufgebaut haben, dass es aus wahren Aussagen keine Falschheit erzeugen kann. Die Quelle der Falschheit, die wir in der indirekten Ableitung erzeugen, muss daher eine Falschheit sein, die wir unserem Argument hinzugefügt haben. Und was wir zu unserem Argument hinzugefügt haben, ist die Ablehnung der Schlussfolgerung. Daher muss die Schlussfolgerung wahr sein.,
Die Form des Arguments ist wie folgt:

Traditionell wurde die Annahme für indirekte Ableitung auch allgemein als „die Annahme für reductio“bezeichnet.
Als konkretes Beispiel können wir unseren verwirrenden Fall beweisen.

Wir haben die Ablehnung unserer Schlussfolgerung in Zeile 4 angenommen. Die Schlussfolgerung, die wir für richtig hielten, war P, und die Ablehnung davon ist P. In Zeile 7 haben wir R bewiesen., Technisch gesehen sind wir an diesem Punkt fertig, aber wir möchten freundlich zu jedem sein, der versucht, unseren Beweis zu verstehen, also wiederholen wir Zeile 3, damit die Sätze R und R nebeneinander stehen, und es ist sehr leicht zu sehen, dass etwas schief gelaufen ist. Das heißt, wenn wir sowohl R als auch R bewiesen haben, haben wir etwas Falsches bewiesen.
Unsere Argumentation geht jetzt so. Was ist schief gelaufen? Zeile 8 ist eine korrekte Verwendung der Wiederholung; Zeile 7 kommt von einer korrekten Verwendung von Modus tollendo ponens; Zeile 6 von einer korrekten Verwendung von Modus ponens; Zeile 5 von einer korrekten Verwendung der doppelten Negation., Wir haben also keinen Fehler in unserer Argumentation gemacht. Wir haben die Zeilen 1, 2 und 3 verwendet, aber das sind Prämissen, von denen wir angenommen haben, dass sie korrekt sind. Dies verlässt Zeile 4. Das muss die Quelle meines Widerspruchs sein. Es muss falsch sein. Wenn Zeile 4 falsch ist, ist P wahr.
Einige Leute halten indirekte Beweise für weniger stark als direkte Beweise. Dafür gibt es viele und komplexe Gründe. Aber für unsere Satzlogik gilt keiner dieser Gründe. Dies liegt daran, dass es möglich ist zu beweisen, dass unsere Satzlogik konsistent ist., Dies bedeutet, es ist möglich zu beweisen, dass unsere Satzlogik keine Lüge beweisen kann, es sei denn, man führt zuerst eine Lüge in das System ein. (Es ist im Allgemeinen nicht möglich zu beweisen, dass leistungsfähigere und fortschrittlichere logische oder mathematische Systeme innerhalb dieser Systeme konsistent sind; Zum Beispiel kann man in der Arithmetik nicht beweisen, dass Arithmetik konsistent ist.) Da wir uns der Konsistenz der Satzlogik sicher sein können, können wir sicher sein, dass in unserer Satzlogik ein indirekter Beweis eine gute Form der Argumentation ist., Wir wissen, dass wir, wenn wir eine Lüge beweisen, eine Lüge hineinlegen müssen; und wenn wir uns über alle anderen Annahmen (dh die Prämissen) unseres Beweises mit Ausnahme der Annahme für indirekte Ableitung sicher sind, können wir zuversichtlich sein, dass diese Annahme für indirekte Ableitung die Quelle der Lüge sein muss.
Hier ist ein Hinweis zur Terminologie erforderlich. Das Wort „Widerspruch“ wird in den meisten logischen Diskussionen mehrdeutig verwendet. Es kann eine Situation bedeuten, wie wir oben sehen, in der zwei Sätze behauptet werden, und diese Sätze können nicht beide wahr sein., Oder es kann einen einzigen Satz bedeuten, der nicht wahr sein kann. Ein Beispiel für einen solchen Satz ist (P^P)., Die Wahrheitstabelle für diesen Satz lautet:
| P | P | (P ^ P) |
|---|---|---|
| T | F | F |
| F | T | F |
Daher kann diese Art von Satz niemals wahr sein, unabhängig von der Bedeutung von P.,
Um Mehrdeutigkeiten zu vermeiden, werden wir in diesem Text immer einen einzelnen Satz, der nicht wahr sein kann, als „widersprüchlichen Satz“bezeichnen. Somit ist (P^P) ein widersprüchlicher Satz. Situationen, in denen zwei Sätze behauptet werden, die nicht beide wahr sein können, werden als „Widerspruch“bezeichnet.
In unserem Beispiel und anderen Beispielen
können wir jetzt eine Version von Galileos Argument rekonstruieren. Wir werden den folgenden Schlüssel verwenden.
P: Es gibt tatsächliche Unendlichkeiten (einschließlich der natürlichen Zahlen und der Quadratzahlen).,
Q: Es gibt eine Eins-zu-Eins-Entsprechung zwischen den natürlichen Zahlen und den quadratischen Zahlen.
R: Die Größe der Menge der natürlichen Zahlen und die Größe der Menge der Quadratzahlen sind gleich.
S: Alle Quadratzahlen sind natürliche Zahlen.
T: Einige der natürlichen Zahlen sind keine quadratischen Zahlen.
U: Es gibt mehr Natürliche zahlen als Quadratzahlen.,
Mit diesem Schlüssel wird das Argument übersetzt:
(P→Q)
(Q→R)
(P→(S^T))
((S^T)→U)
(U→R)
P
Und wir können beweisen, dass dies ein gültiges Argument ist, indem wir indirekte Ableitung verwenden:
In Zeile 6 nahmen wir P an, weil Galileo das P glaubte und beweisen wollte, dass P. Das heißt, er glaubte, dass es keine tatsächlichen Unendlichkeiten gibt, und nahm an, dass es falsch war zu glauben, dass es nicht der Fall ist, dass es keine tatsächlichen Unendlichkeiten gibt. Diese Falschheit wird zu anderen Falschheiten führen und sich selbst aufdecken.,
Für Interessierte: Galileo kam zu dem Schluss, dass es keine tatsächlichen Unendlichkeiten, sondern potentielle Unendlichkeiten gibt. So argumentierte er, es ist nicht der Fall, dass alle natürlichen Zahlen existieren (in gewissem Sinne von „existieren“), aber es ist wahr, dass Sie natürliche Zahlen für immer zählen könnten. Viele Philosophen vor und nach Galileo hielten diese Ansicht; Es ähnelt einer Ansicht von Aristoteles, der ein wichtiger Logiker und Philosoph war, der fast zweitausend Jahre vor Galileo schrieb.,
Beachten Sie, dass Sie in einem solchen Argument argumentieren könnten, dass nicht die Annahme für die indirekte Ableitung, sondern eine der Prämissen die Quelle des Widerspruchs war. Heute glauben die meisten Mathematiker dies an Galileos Argument. Ein Logiker und Mathematiker namens Georg Cantor (1845-1918), der Erfinder der Mengenlehre, argumentierte, dass unendliche Mengen richtige Teilmengen gleicher Größe haben können., Das heißt, Cantor bestritt Prämisse 4 oben: Obwohl alle Quadratzahlen natürliche Zahlen sind und nicht alle natürlichen Zahlen quadratische Zahlen sind, ist es nicht der Fall, dass diese beiden Sätze unterschiedlich groß sind. Cantor akzeptierte jedoch die Prämisse 2 oben und glaubte daher, dass die Größe der Menge natürlicher Zahlen und die Größe der Menge quadratischer Zahlen gleich sind. Heute studieren Mathematiker und Logiker mit Cantors Argumentation die Unendlichkeit und haben ein großes Wissen über die Natur der Unendlichkeit entwickelt. Wenn Sie dies interessiert, siehe Abschnitt 17.5.,
betrachten wir ein weiteres Beispiel zur Veranschaulichung der indirekten Ableitung. Ein sehr nützlicher Satz von Theoremen wird heute nach dem Logiker Augustus De Morgan (1806-1871) „De Morgans Theoreme“ genannt. Wir können diese erst in Kapitel 9 vollständig angeben, aber wir können ihr Äquivalent auf Englisch angeben: DeMorgan hat festgestellt, dass (PvQ) und (P^Q) äquivalent sind und dass (P^Q) und (PvQ) äquivalent sind. Angesichts dessen sollte es ein Satz unserer Sprache sein, der ((PvQ)→(P^Q)). Lass uns das beweisen.
Die gesamte Formel ist eine Bedingung, daher verwenden wir eine bedingte Ableitung., Unser Beweis muss also beginnen:
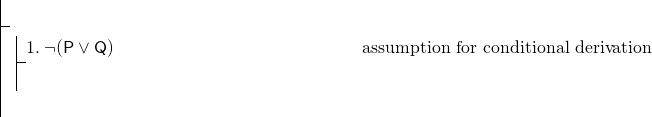
Um die bedingte Ableitung abzuschließen, müssen wir beweisen (P^Q). Dies ist eine Konjunktion, und unsere Regel zum Anzeigen von Konjunktionen ist die Adjunktion. Da die Verwendung dieser Regel möglicherweise der beste Weg ist, um (P^Q) anzuzeigen, können wir darauf abzielen, P und dann Q anzuzeigen und dann die Adjunktion durchzuführen. Aber wir haben offensichtlich sehr wenig zu arbeiten—nur Zeile 1, was eine Negation ist. In einem solchen Fall ist es normalerweise ratsam, einen indirekten Beweis zu versuchen. Beginnen Sie mit einem indirekten Nachweis von P.,

Wir müssen jetzt einen Widerspruch finden—jeden Widerspruch. Aber es gibt schon eine offensichtliche. Zeile 1 besagt, dass weder P noch Q wahr sind. Aber Zeile 3 sagt, dass P wahr ist. Wir müssen diesen Widerspruch deutlich machen, indem wir eine Formel und ihre Ablehnung finden. Wir können dies mit Addition tun.

Um den Beweis abzuschließen, werden wir diese Strategie erneut verwenden.

Wir werden De Morgans Theoreme als Probleme für Kapitel 9 beweisen.,
Hier ist eine allgemeine Faustregel für Beweise: Wenn Sie eine Bedingung beweisen, führen Sie immer eine bedingte Ableitung durch; andernfalls versuchen Sie es mit direkter Ableitung; Wenn das fehlschlägt, versuchen Sie es mit indirekter Ableitung.
8.4 Probleme
- füllen Sie die folgenden Beweise. Jeder erfordert eine indirekte Ableitung. Die letzten beiden sind herausfordernd.
- Beweisen die folgenden sind theoreme.
- (P^P).
- ((P→P)^(P→P)).
- (P→(P^Q)).
- ((P^Q)→(P→Q)).
- Schreiben Sie in normalem umgangssprachlichem Englisch Ihr eigenes gültiges Argument mit mindestens zwei Prämissen., Ihr Argument sollte nur ein Absatz sein (keine geordnete Liste von Sätzen oder irgendetwas anderes, das wie formale Logik aussieht). Übersetzen Sie es in Satzlogik und beweisen Sie, dass es mit einer indirekten Ableitung gültig ist.
Diese Übersetzung des Titels von Galileos Buch ist die häufigste geworden, obwohl eine wörtliche mathematische Diskurse und Demonstrationen gewesen wäre. Übersetzungen des Buches umfassen Drake (1974).