Der α-Koeffizient ist die am weitesten verbreitete Verfahren für die Abschätzung der Zuverlässigkeit der angewandten Forschung. Wie von Sijtsma (2009) angegeben, ist seine Popularität so, dass Cronbach (1951) häufiger als Referenz zitiert wurde als der Artikel über die Entdeckung der DNA-Doppelhelix., Dennoch sind seine Grenzen bekannt (Lord und Novick, 1968; Cortina, 1993; Yang und Green, 2011), einige der wichtigsten sind die Annahmen von nicht korrelierten Fehlern, Tau-Äquivalenz und Normalität.
Die Annahme unkorrelierter Fehler (der Fehlerwert eines beliebigen Elementpaares ist unkorreliert) ist eine Hypothese der klassischen Testtheorie (Lord und Novick, 1968), deren Verletzung das Vorhandensein komplexer mehrdimensionaler Strukturen implizieren kann, die Schätzverfahren erfordern, die diese Komplexität berücksichtigen (z. B. Tarkkonen und Vehkalahti, 2005; Green und Yang, 2015)., Es ist wichtig, den falschen Glauben zu entwurzeln, dass der α-Koeffizient ein guter Indikator für die Unidimensionalität ist, da sein Wert höher wäre, wenn die Skala unidimensional wäre. Tatsächlich ist genau das Gegenteil der Fall, wie Sijtsma (2009) gezeigt hat, und seine Anwendung unter solchen Bedingungen kann dazu führen, dass die Zuverlässigkeit stark überschätzt wird (Raykov, 2001). Folglich muss vor der Berechnung α überprüft werden, ob die Daten zu unidimensionalen Modellen passen.= = = tau-Äquivalenz = = = Die Tau-Äquivalenz wird als Tau-Äquivalenz bezeichnet., die gleiche true-score für alle Prüflinge, – oder-gleich-Faktor-Ladungen aller Elemente in einer Faktoren-Modell) ist eine Voraussetzung für α äquivalent der Zuverlässigkeit Koeffizient (Cronbach, 1951). Wenn die Annahme der Tau-Äquivalenz verletzt wird, wird der wahre Zuverlässigkeitswert (Raykov, 1997; Graham, 2006) um einen Betrag unterschätzt, der je nach Schwere des Verstoßes zwischen 0,6 und 11,1% variieren kann (Green und Yang, 2009a). Das Arbeiten mit Daten, die dieser Annahme entsprechen, ist in der Praxis im Allgemeinen nicht praktikabel (Teo und Fan, 2013); das kongenere Modell (dh,, verschiedene Faktorladungen) ist die realistischere.
Die Anforderung an multivariante Normalität ist weniger bekannt und beeinflusst sowohl die puntuelle Zuverlässigkeitsschätzung als auch die Möglichkeit, Konfidenzintervalle festzulegen (Dunn et al., 2014). Sheng und Sheng (2012) beobachteten kürzlich, dass, wenn die Verteilungen verzerrt und/oder leptokurtisch sind, eine negative Verzerrung erzeugt wird, wenn der Koeffizient α berechnet wird; Ähnliche Ergebnisse wurden von Green und Yang (2009b) in einer Analyse der Auswirkungen von nicht-normalen Verteilungen bei der Schätzung der Zuverlässigkeit präsentiert., Die Untersuchung von Schiefheitsproblemen ist wichtiger, wenn wir sehen, dass Forscher in der Praxis gewöhnlich mit schiefen Skalen arbeiten (Micceri, 1989; Norton et al., 2013; Ho und Yu, 2014). Zum Beispiel schätzte Micceri (1989), dass etwa 2/3 der Fähigkeit und über 4/5 der psychometrischen Messungen eine zumindest mäßige Asymmetrie aufwiesen (dh Schiefe um 1). Trotzdem wurde der Einfluss der Schiefe auf die Zuverlässigkeitsschätzung wenig untersucht.,
In Anbetracht der reichlich vorhandenen Literatur über die Grenzen und Verzerrungen des α-Koeffizienten (Revelle und Zinbarg, 2009; Sijtsma, 2009, 2012; Cho und Kim, 2015; Sijtsma und van der Ark, 2015) stellt sich die Frage, warum Forscher weiterhin α verwenden, wenn alternative Koeffizienten existieren, die diese Grenzen überwinden. Es ist möglich, dass der Überschuss an Verfahren zur Schätzung der Zuverlässigkeit, der im letzten Jahrhundert entwickelt wurde, die Debatte entfacht hat. Dies wäre durch die Einfachheit der Berechnung dieses Koeffizienten und seine Verfügbarkeit in kommerzieller Software noch verstärkt worden.,
Die Schwierigkeit, den Zuverlässigkeitskoeffizienten des pxx zu schätzen, liegt in seiner Definition pxx ‚ =σt2∕σx2, die den wahren Wert im Varianzzähler enthält, wenn dieser von Natur aus nicht beobachtbar ist. Der α-Koeffizient versucht, diese nicht beobachtbare Abweichung von der Kovarianz zwischen den Elementen oder Komponenten anzunähern. Cronbach (1951) zeigte, dass in Abwesenheit von tau-Äquivalenz, der α-Koeffizient (oder Guttman Lambda 3, die äquivalent zu α ist) war eine gute Untergrenze Annäherung., Wenn also die Annahmen verletzt werden, führt das Problem dazu, dass die bestmögliche Untergrenze gefunden wird.In der Tat wird dieser Name der Methode mit der größten Untergrenze (GLB) gegeben, die aus theoretischer Sicht die bestmögliche Annäherung darstellt (Jackson und Agunwamba, 1977; Woodhouse und Jackson, 1977; Shapiro und ten Berge, 2000; Sočan, 2000; ten Berge und Sočan, 2004; Sijtsma, 2009). Revelle und Zinbarg (2009) sind jedoch der Ansicht, dass ω eine bessere untere Grenze als GLB ergibt., Es gibt daher eine ungelöste Debatte darüber, welche dieser beiden Methoden die beste Untergrenze bietet; Darüber hinaus wurde die Frage der Nicht-Normalität nicht erschöpfend untersucht, wie in der vorliegenden Arbeit diskutiert.
ω-Koeffizienten
McDonald (1999) schlug den wt-Koeffizienten zur Schätzung der Zuverlässigkeit aus einem faktoriellen Analyserahmen vor, der formell ausgedrückt werden kann als:
Wobei λj das Laden von Element j ist, λj2 die Gemeinschaftlichkeit von Element j ist und ψ der Einzigartigkeit entspricht., Der wt-Koeffizient ist durch Einbeziehung der Lambdas in seine Formeln sowohl geeignet, wenn tau-Äquivalenz (dh Gleichfaktorladungen aller Testelemente) vorhanden ist (wt stimmt mathematisch mit α überein), als auch wenn Elemente mit unterschiedlichen Diskriminierungen in der Darstellung des Konstrukts vorhanden sind (dh unterschiedliche Faktorladungen der Elemente: kongenere Messungen). Folglich korrigiert wt die Unterschätzungsverzerrung von α, wenn die Annahme der Tau-Äquivalenz verletzt wird (Dunn et al., 2014) und verschiedene Studien zeigen, dass es eine der besten Alternativen zur Schätzung der Zuverlässigkeit ist (Zinbarg et al.,, 2005, 2006; Revelle und Zinbarg, 2009), obwohl bis heute seine Funktionsweise unter Bedingungen der Schiefe unbekannt ist.
Wenn eine Korrelation zwischen Fehlern besteht oder mehr als eine latente Dimension in den Daten vorhanden ist, wird der Beitrag jeder Dimension zur erklärten Gesamtvarianz geschätzt, wobei das sogenannte hierarchische ω (wh) erhalten wird, das es uns ermöglicht, die schlechteste Überschätzungsneigung von α mit mehrdimensionalen Daten zu korrigieren (siehe Tarkkonen und Vehkalahti, 2005; Zinbarg et al., 2005; Revelle und Zinbarg, 2009)., Die Koeffizienten wh und wt sind in unidimensionalen Daten äquivalent, daher beziehen wir uns auf diesen Koeffizienten einfach als ω.
Greatest Lower Bound (GLB)
Sijtsma (2009) zeigt in einer Reihe von Studien, dass einer der stärksten Zuverlässigkeitsschätzer GLB ist—abgeleitet von Woodhouse und Jackson (1977) aus den Annahmen der klassischen Testtheorie (Cx = Ct + Ce)—eine Inter-Item-Kovarianzmatrix für beobachtete Item-Scores Cx. Es gliedert sich in zwei Teile: die Summe der Inter-Item-Kovarianzmatrix für Item true Scores Ct; und die Inter-Item-Fehlerkovarianzmatrix Ce (ten Berge und Sočan, 2004)., Sein Ausdruck ist:
wobei σx2 die Testvarianz ist und tr (Ce) sich auf die Spur der Interelement-Fehlerkovarianzmatrix bezieht, die sich als so schwer abzuschätzen erwiesen hat. Eine Lösung bestand darin, faktorielle Verfahren wie die Minimalrangfaktoranalyse (ein als glb bekanntes Verfahren) zu verwenden.fa). In jüngerer Zeit wurde das GLB – algebraische Verfahren (GLBa) aus einem von Andreas Moltner entwickelten Algorithmus entwickelt (Moltner und Revelle, 2015)., Laut Revelle (2015a) nimmt dieses Verfahren die Form an, die der ursprünglichen Definition von Jackson und Agunwamba (1977) am treuesten ist, und es hat den zusätzlichen Vorteil, einen Vektor einzuführen, um die Elemente nach Wichtigkeit zu gewichten (Al-Homidan, 2008).
Trotz seiner theoretischen Stärken wurde GLB nur sehr wenig verwendet, obwohl einige neuere empirische Studien gezeigt haben, dass dieser Koeffizient bessere Ergebnisse liefert als α (Lila et al., 2014) und α und ω (Wilcox et al., 2014)., Dennoch neigt es in kleinen Stichproben unter der Annahme der Normalität dazu, den wahren Zuverlässigkeitswert zu überschätzen (Shapiro und ten Berge, 2000); Seine Funktionsweise unter nicht normalen Bedingungen bleibt jedoch unbekannt, insbesondere wenn die Verteilungen der Elemente asymmetrisch sind.
Unter Berücksichtigung der oben definierten Koeffizienten und der Vorurteile und Einschränkungen der einzelnen Koeffizienten besteht das Ziel dieser Arbeit darin, die Robustheit dieser Koeffizienten bei Vorhandensein asymmetrischer Elemente unter Berücksichtigung der Annahme der Tau-Äquivalenz und der Stichprobengröße zu bewerten.,
Methoden
Datengenerierung
Die Daten wurden mit der Software R (R Development Core Team, 2013) und RStudio (Racine, 2012) nach dem faktoriellen Modell generiert:
wobei Xij die simulierte Antwort von Subjekt i in Punkt j, λjk ist das Laden von Element j in Faktor k (der durch das unifaktorielle Modell erzeugt wurde); Fk ist der latente Faktor, der durch eine standardisierte Normalverteilung (Mittelwert 0 und Varianz 1) erzeugt wird, und ej ist der zufällige Messfehler jedes Elements, der auch einer standardisierten Normalverteilung folgt.,
Verzerrte Elemente: Standardmäßige normale Xij wurden transformiert, um nicht-normale Verteilungen mit dem von Headrick (2002) vorgeschlagenen Verfahren zu erzeugen, indem Polynomtransformationen fünfter Ordnung angewendet wurden:
Simulierte Bedingungen
Um die Leistung der Zuverlässigkeitskoeffizienten (α, ω, GLB und GLBa) Wir arbeiteten mit drei Stichprobengrößen (250, 500, 1000), zwei Testgrößen: kurz (6 Artikel) und lang (12 Artikel), zwei Bedingungen der Tau-Äquivalenz (eine mit Tau-Äquivalenz und eine ohne, d.h.,, kongenial) und die fortschreitende Einbeziehung asymmetrischer Elemente (von allen Elementen normal bis zu allen Elementen asymmetrisch). Im Kurztest wurde die Zuverlässigkeit auf 0,731 eingestellt, was bei Vorliegen der Tau-Äquivalenz mit sechs Elementen mit Faktorladungen = 0,558 erreicht wird; während das kongenere Modell durch Setzen von Faktorladungen bei Werten von 0.3, 0.4, 0.5, 0.6, 0.7, und 0,8 (siehe Anhang I). Im langen Test von 12 Items wurde die Zuverlässigkeit auf 0 gesetzt.,845, wobei die gleichen Werte wie im Kurztest sowohl für die Tau-Äquivalenz als auch für das kongenerierte Modell verwendet wurden (in diesem Fall gab es zwei Elemente für jeden Lambda-Wert). Auf diese Weise wurden 120 Bedingungen mit jeweils 1000 Replikaten simuliert.
Datenanalyse
Die Hauptanalysen wurden unter Verwendung der Pakete Psych (Revelle, 2015b) und GPArotation (Bernaards und Jennrich, 2015) durchgeführt, mit denen α und ω geschätzt werden können. Zur Schätzung von GLB wurden zwei computergestützte Ansätze verwendet: glb.fa (Revelle, 2015a) und glb.,algebraisch (Moltner und Revelle, 2015), letztere arbeiteten von Autoren wie Hunt und Bentler (2015).
Um die Genauigkeit der verschiedenen Schätzer bei der Wiederherstellung der Zuverlässigkeit zu bewerten, haben wir das Root Mean Square of Error (RMSE) und die Verzerrung berechnet. Der erste ist der Mittelwert der Unterschiede zwischen der geschätzten und der simulierten Zuverlässigkeit und wird wie folgt formalisiert:
wobei ρ^ die geschätzte Zuverlässigkeit für jeden Koeffizienten ist, ρ die simulierte Zuverlässigkeit und Nr die Anzahl der Replikate., Die % – Verzerrung wird als Differenz zwischen dem Mittelwert der geschätzten Zuverlässigkeit und der simulierten Zuverlässigkeit verstanden und definiert als:
Je größer der Wert in beiden Indizes ist, desto größer ist die Ungenauigkeit des Schätzers, aber im Gegensatz zu RMSE kann die Verzerrung positiv oder negativ sein; In diesem Fall würden zusätzliche Informationen darüber erhalten, ob der Koeffizient den simulierten Zuverlässigkeitsparameter unterschätzt oder überschätzt., Auf Empfehlung von Hoogland und Boomsma (1998) wurden Werte von RMSE < 0.05 und % bias < 5% als akzeptabel angesehen.
Ergebnisse
Die wichtigsten Ergebnisse sind in Tabelle 1 (6 Punkte) und Tabelle 2 (12 Punkte) zu sehen. Diese zeigen die RMSE – und % – Verzerrung der Koeffizienten in Tau-Äquivalenz-und kongenerierten Bedingungen und wie die Schiefe der Testverteilung mit dem allmählichen Einbau asymmetrischer Elemente zunimmt.
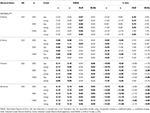
Tabelle 1., RMSE und Bias mit Tau-Äquivalenz und kongenialem Zustand für 6 Artikel, drei Stichprobengrößen und die Anzahl der schiefen Artikel.
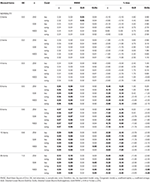
Tabelle 2. RMSE und Bias mit Tau-Äquivalenz und kongenialem Zustand für 12 Artikel, drei Stichprobengrößen und die Anzahl der schiefen Artikel.
Nur unter Bedingungen der tau-Äquivalenz und Normalität (skewness < 0.2) wird beobachtet,dass der α-Koeffizient die simulierte Zuverlässigkeit korrekt schätzt, wie ω., Im kongenerialen Zustand korrigiert ω die Unterschätzung von α. Sowohl GLB als auch GLBa weisen unter Normalität eine positive Verzerrung auf, GLBa zeigt jedoch annähernd ½ weniger % Verzerrung als GLB (siehe Tabelle 1). Wenn wir die Probengröße betrachten, beobachten wir, dass mit zunehmender Testgröße die positive Verzerrung von GLB und GLBa abnimmt, aber niemals verschwindet.
Unter asymmetrischen Bedingungen sehen wir in Tabelle 1, dass sowohl α als auch ω eine inakzeptable Leistung mit zunehmender RMSE und Unterschätzung aufweisen, die eine Vorspannung erreichen können > 13% für den α-Koeffizienten (zwischen 1 und 2% niedriger für ω)., Die GLB-und GLBa-Koeffizienten weisen eine niedrigere RMSE auf, wenn die Testschräge oder die Anzahl der asymmetrischen Elemente zunimmt (siehe Tabellen 1, 2). Der GLB-Koeffizient liefert bessere Schätzungen, wenn der Testspießwert des Tests etwa 0,30 beträgt; GLBa ist sehr ähnlich und präsentiert bessere Schätzungen als ω mit einem Testspießwert um 0,20 oder 0,30. Wenn der schiefe Wert jedoch auf 0,50 oder 0,60 ansteigt, bietet GLB eine bessere Leistung als GLBa. Die Testgröße (6 oder 12 Einheiten) hat einen viel wichtigeren Effekt als die Stichprobengröße auf die Genauigkeit der Schätzungen.,
Diskussion
In dieser Studie wurden vier Faktoren manipuliert: tau-Äquivalenz oder kongeniertes Modell, Stichprobengröße (250, 500 und 1000), Anzahl der Testelemente (6 und 12) und Anzahl der asymmetrischen Elemente (von 0 asymmetrischen Elementen bis zu allen asymmetrischen Elementen), um die Robustheit des Vorhandenseins asymmetrischer Daten in den vier analysierten Zuverlässigkeitskoeffizienten zu bewerten. Diese Ergebnisse werden im Folgenden diskutiert.,
Unter den Bedingungen der Tau-Äquivalenz konvergieren die α-und ω-Koeffizienten, aber in Abwesenheit der Tau-Äquivalenz (kongeneric) weist ω immer bessere Schätzungen und kleinere RMSE-und % – Verzerrungen auf als α. In diesem realistischeren Zustand (Grün und Yang, 2009a; Yang und Grün, 2011) wird α daher zu einem negativ voreingenommenen Zuverlässigkeitsschätzer (Graham, 2006; Sijtsma, 2009; Cho und Kim, 2015) und ω ist immer α vorzuziehen (Dunn et al., 2014). Im Falle der Nichtverletzung der Normalitätsannahme ist ω der beste Schätzer aller ausgewerteten Koeffizienten (Revelle und Zinbarg, 2009).,
Wenn wir uns der Stichprobengröße zuwenden, stellen wir fest, dass dieser Faktor einen geringen Effekt unter der Normalität oder eine leichte Abweichung von der Normalität hat: Die RMSE und die Verzerrung nehmen mit zunehmender Stichprobengröße ab. Dennoch kann man sagen, dass wir für diese beiden Koeffizienten mit Stichprobengröße von 250 und Normalität relativ genaue Schätzungen erhalten (Tang und Cui, 2012; Javali et al., 2011)., Bei den GLB-und GLBa-Koeffizienten neigen RMSE und BIAS mit zunehmender Stichprobengröße dazu, abzunehmen; Sie behalten jedoch auch bei großen Stichprobengrößen von 1000 eine positive Tendenz für den Normalitätszustand bei (Shapiro und ten Berge, 2000; ten Berge und Sočan, 2004; Sijtsma, 2009).
Für die Testgröße beobachten wir im Allgemeinen eine höhere RMSE und Bias mit 6 Elementen als mit 12, was darauf hindeutet, dass je höher die Anzahl der Elemente, desto niedriger die RMSE und die Bias der Schätzer (Cortina, 1993). Im Allgemeinen wird der Trend sowohl für 6 als auch für 12 Artikel beibehalten.,
Wenn wir uns den Effekt der fortschreitenden Einbeziehung asymmetrischer Elemente in den Datensatz ansehen, stellen wir fest, dass der α-Koeffizient für asymmetrische Elemente sehr empfindlich ist; Diese Ergebnisse ähneln denen von Sheng und Sheng (2012) und Green und Yang (2009b). Der Koeffizient ω weist ähnliche RMSE-und Bias-Werte wie α auf, ist jedoch selbst bei Tau-Äquivalenz etwas besser. GLB und GLBa liefern bessere Schätzungen, wenn die Testschärfe von Werten nahe 0 abweicht.
Wenn man bedenkt, dass es in der Praxis üblich ist, asymmetrische Daten zu finden (Micceri, 1989; Norton et al.,, 2013; Ho und Yu, 2014), Sijtsma“s Vorschlag (2009) mit GLB als eine Zuverlässigkeit estimator erscheint gut begründet. Andere Autoren, wie Revelle und Zinbarg (2009) und Green und Yang (2009a), empfehlen die Verwendung von ω, jedoch führte dieser Koeffizient nur zu guten Ergebnissen im Zustand der Normalität oder mit geringem Anteil an schiefen Elementen. In jedem Fall zeigten diese Koeffizienten größere theoretische und empirische Vorteile als α. Dennoch empfehlen wir Forschern, nicht nur pünktliche Schätzungen zu untersuchen, sondern auch Intervallschätzungen zu verwenden (Dunn et al., 2014).,
Diese Ergebnisse sind auf die simulierten Bedingungen beschränkt und es wird davon ausgegangen, dass keine Korrelation zwischen Fehlern besteht. Dies würde es erforderlich machen, weitere Untersuchungen durchzuführen, um die Funktionsweise der verschiedenen Zuverlässigkeitskoeffizienten mit komplexeren mehrdimensionalen Strukturen (Reise, 2012; Green und Yang, 2015) und in Gegenwart von ordinalen und/oder kategorialen Daten zu bewerten, bei denen die Nichteinhaltung der Annahme von Normalität die Norm ist.
Schlussfolgerung
Wenn die gesamten Testergebnisse normal verteilt sind (dh,(alle Elemente sind normalerweise verteilt) ω sollte die erste Wahl sein, gefolgt von α, da sie die von GLB vorgestellten Überschätzungsprobleme vermeiden. Wenn jedoch eine geringe oder mäßige Testschärfe vorliegt, sollte GLBa verwendet werden. GLB wird empfohlen, wenn der Anteil asymmetrischer Elemente hoch ist, da unter diesen Bedingungen die Verwendung von α und ω als Zuverlässigkeitsschätzer unabhängig von der Stichprobengröße nicht ratsam ist.
Autorenbeiträge
Entwicklung der Idee von Forschung und theoretischem Rahmen (IT, JA). Aufbau des methodischen Rahmens (IT, JA)., Entwicklung der R-Sprachsyntax (IT, JA). Datenanalyse und Interpretation von Daten (IT, JA). Diskussion der Ergebnisse vor dem Hintergrund aktueller theoretischer Hintergründe (JA, IT). Vorbereitung und verfassen des Artikels (JA, SIE). Im Allgemeinen haben beide Autoren gleichermaßen zur Entwicklung dieser Arbeit beigetragen.,
Förderung
Der Erstautor hat folgende finanzielle Unterstützung für die Forschung, die Urheberschaft und/oder Veröffentlichung dieses Artikels erhalten: ER erhielt finanzielle Unterstützung von der chilenischen Nationalen Kommission für wissenschaftliche und technologische Forschung (CONICYT) „Becas Chile“ Promotionsprogramm (Grant no: 72140548).
Interessenkonflikterklärung
Die Autoren erklären, dass die Untersuchung ohne kommerzielle oder finanzielle Beziehungen durchgeführt wurde, die als potenzieller Interessenkonflikt ausgelegt werden könnten.
Cronbach, L. (1951)., Koeffizient alpha und die interne Struktur der Tests. Psychometrika 16, 297-334. doi: 10.1007 / BF02310555
CrossRef Volltext / Google Scholar
McDonald, R. (1999). Testtheorie: eine einheitliche Behandlung. Mahwah, NJ: Lawrence Erlbaum Associates.
Google Scholar
R Development Core Team (2013). R: Eine Sprache und Umgebung für die statistische Berechnung. Wien: R Foundation for Statistical Computing.
Raykov, T. (1997)., Scale reliability, cronbach“s coefficient alpha, and violations of essential tau- equivalence with fixed congeneric components. Multivariate Behav. Res. 32, 329–353. doi: 10.1207/s15327906mbr3204_2
PubMed Abstract | CrossRef Full Text | Google Scholar
Raykov, T. (2001). Bias of coefficient alpha for fixed congeneric measures with correlated errors. Appl. Psychol. Meas. 25, 69–76. doi: 10.1177/01466216010251005
CrossRef Full Text | Google Scholar
Revelle, W. (2015b). Package „psych.,“Online verfügbar unter: http://org/r/psych-manual.pdf
Shapiro, A., und ten Berge, J. M. F. (2000). Die asymptotische Verzerrung der minimalen Spurenfaktoranalyse, mit Anwendungen auf die größte untere Grenze zur Zuverlässigkeit. Psychometrika 65, 413-425. doi: 10.1007/BF02296154
CrossRef Full Text | Google Scholar
ten Berge, J. M. F., und Sočan, G. (2004). Die größte Untergrenze für die Zuverlässigkeit eines Tests und die Hypothese der Unidimensionalität. Psychometrika 69, 613-625. doi: 10.,1007 / BF02289858
CrossRef Volltext / Google Scholar
Woodhouse, B. und Jackson, P. H. (1977). Untere Grenzen für die Zuverlässigkeit der Gesamtpunktzahl bei einem Test, der aus nicht homogenen Elementen besteht: II: ein Suchverfahren zum Auffinden der größten Untergrenze. Psychometrika 42, 579-591. doi: 10.1007 / BF02295980
CrossRef Volltext / Google Scholar
Anhang I
R Syntax Zuverlässigkeitskoeffizienten von Pearson Korrelationsmatrizen zu schätzen., Die Korrelationswerte außerhalb der Diagonale werden berechnet, indem die Faktorbeladung der Elemente multipliziert wird: (1) tau-äquivalentes Modell Sie sind alle gleich 0.3114 (λiλj = 0.558 × 0.558 = 0.3114) und (2) kongenerisches Modell Sie variieren als Funktion der verschiedenen Faktorbeladung (z. B. das Matrixelement a1, 2 = λ1λ2 = 0.3 × 0.4 = 0.12). In beiden Beispielen beträgt die wahre Zuverlässigkeit 0,731.
> omega(Cr,1)$alpha # standardisiertes Cronbach“s α
0.731
> omega(Cr,1)$omega.tot # Koeffizient ω Gesamt
0.,731
> glb.fa(Cr)$glb # GLB factorial procedure
0.731
> glb.algebraic(Cr)$glb # GLB algebraic procedure
0.731
> omega(Cr,1)$alpha # standardized Cronbach“s α
0.717
> omega(Cr,1)$omega.tot # coefficient ω total
0.731
> glb.fa(Cr)$glb # GLB factorial procedure
0.754
> glb.algebraic(Cr)$glb # GLB algebraic procedure
0.731