Inhalt – Wahrscheinlichkeits-Dichte-Funktionen

Inhalt

Wahrscheinlichkeits-Dichte-Funktionen

Die Wahrscheinlichkeits-Dichte-Funktion (pdf) \(f(x)\) einer kontinuierlichen Zufallsvariablen \(X\) ist definiert als die Ableitung der cdf – \(F(x)\):

\

manchmal ist Es sinnvoll, die cdf – \(F(x)\) in Bezug auf die pdf \(f(x)\):

\

Die pdf \(f(x)\) hat zwei wichtige Eigenschaften:

1. \(f(x) \geq 0\) für alle \(x\)
2. \(\displaystyle\int_{-\infty}^{\infty} f(x)\;dx = 1\).,

Eine unendliche Formenvielfalt ist für eine PDF-Datei möglich, da nur die beiden oben genannten Eigenschaften erforderlich sind. Das PDF kann einen oder mehrere Peaks oder gar keine Peaks haben; es kann Diskontinuitäten haben, aus Kombinationen von Funktionen bestehen und so weiter. abbildung 5 zeigt ein PDF mit einem einzigen Peak und einer leichten Schiefe. Wie bei einer typischen PDF-Datei nähert sich der Wert der Funktion Null als \(x \to \infty\) und \(x \to -\infty\).

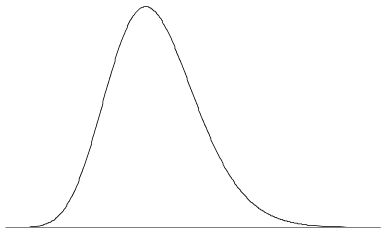
Abbildung 5: Ein PDF kann ungefähr so aussehen.,

Wir untersuchen nun, wie sich die Wahrscheinlichkeiten bezüglich der kontinuierlichen Zufallsvariablen \(X\) auf ihre Größe beziehen. Das wichtige Ergebnis hier ist, dass

\_a^b.\]

Dieses Ergebnis ergibt sich aus der Tatsache, dass beide Seiten gleich \(F(b) – F(a)\).

Notizen.

• Für eine kontinuierliche Zufallsvariable müssen wir die Wahrscheinlichkeit berücksichtigen, dass sie in einem Intervall liegt. Die Bedeutung dieses Ergebnisses ist, dass es uns sagt, dass wir, um die Wahrscheinlichkeit zu finden, den Bereich unter dem PDF im gegebenen Intervall finden müssen.
• Die Gesamtfläche unter dem PDF ist gleich 1., Dieses Ergebnis sagt uns also, dass wir, um die Wahrscheinlichkeit zu approximieren, dass die Zufallsvariable in einem bestimmten Intervall liegt, nur den Bruchteil der Fläche unter dem PDF zwischen den Enden des Intervalls erraten müssen.
• Dieses Ergebnis bietet eine weitere Perspektive, warum PDFs nicht negativ sein können, da sonst eine negative Wahrscheinlichkeit erhalten werden könnte, was unmöglich ist.
• Die PDF-Datei ist analog zur Wahrscheinlichkeitsfunktion (pf) für eine diskrete Zufallsvariable, unterscheidet sich jedoch von dieser. Ein pf gibt eine Wahrscheinlichkeit an, daher kann er nicht größer als eins sein., Ein pdf \(f(x)\) kann jedoch für einige Werte von \(x\) einen Wert größer als einen Wert angeben, da es sich nicht um den Wert von \(f (x)\) handelt, sondern um den Bereich unter der Kurve, der die Wahrscheinlichkeit darstellt. Andererseits spiegelt die Höhe der Kurve die relative Wahrscheinlichkeit wider. Wenn \(f(b) = 2f(a)\), dann ist eine Beobachtung, die sich in der Nähe von \(b\) ist ungefähr doppelt so wahrscheinlich, wie eine Beobachtung, die sich in der Nähe von \(a\).,

Nächste Seite – Inhalt – Mittelwert und Varianz einer kontinuierlichen Zufallsvariablen