
Pythagoras
vor Über 2000 Jahren gab es eine erstaunliche Entdeckung über Dreiecke:
Wenn ein Dreieck einen rechten Winkel (90°) …
… und Quadrate sind auf jeder der drei Seiten gemacht,…
… dann hat das größte Quadrat genau die gleiche Fläche wie die beiden anderen Quadrate zusammen!,
Es heißt „Pythagoras“ Theorem“ und kann in einer kurzen Gleichung geschrieben werden:
a2 + b2 = c2
Hinweis:
- c ist die längste Seite des Dreiecks
- a und b sind die beiden anderen Seiten
Definition
Die längste Seite des Dreiecks wird als „hypotenuse“ bezeichnet, daher lautet die formale Definition:
In einem rechtwinkligen Dreieck:
Das Quadrat der Hypotenuse ist gleich
die Summe der Quadrate der anderen beiden Seiten.,
Sicher … ?
Lassen Sie s sehen, ob es wirklich funktioniert mit einem Beispiel.

Warum Ist Das Nützlich?
Wenn wir die Längen zweier Seiten eines rechtwinkligen Dreiecks kennen, können wir die Länge der dritten Seite ermitteln. (Aber denken Sie daran, es funktioniert nur bei rechtwinkligen Dreiecken!)
Wie benutze ich es?,
Schreiben Sie es als Gleichung auf:
 |
a2 + b2 = c2 |
Dann verwenden wir Algebra, um einen fehlenden Wert zu finden, wie in diesen Beispielen:
Sie können auch über Quadrate und Quadratwurzeln lesen, um herauszufinden, warum √169 = 13
Es funktioniert auch umgekehrt: Wenn die drei Seiten eines Dreiecks a2 + b2 = c2 bilden, ist das Dreieck rechtwinklig.,
Und Sie Können Den Satz Selbst Beweisen !
Holen Sie sich Papierstift und Schere und verwenden Sie dann die folgende Animation als Anleitung:
- Zeichnen Sie ein rechtwinkliges Dreieck auf das Papier und lassen Sie viel Platz.,
- Zeichnen Sie ein Quadrat entlang der Hypotenuse (die längste Seite)
- Zeichnen Sie das gleiche große Quadrat auf der anderen Seite der Hypotenuse
- Zeichnen Sie Linien wie in der Animation gezeigt:

- Schneiden Sie die Formen aus
- Ordnen Sie sie so an, dass Sie nachweisen können, dass das große Quadrat die gleiche Fläche wie die beiden Quadrate auf den anderen Seiten hat
li>
Ein weiterer, erstaunlich einfacher Beweis
Hier ist einer der ältesten Beweise dafür, dass das Quadrat auf der langen Seite die gleiche Fläche wie die anderen Quadrate hat.,
Sehen Sie sich die Animation an und achten Sie darauf, wenn die Dreiecke herumrutschen.
Möglicherweise möchten Sie die Animation einige Male ansehen, um zu verstehen, was passiert.
Das violette Dreieck ist das wichtige.
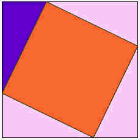 |
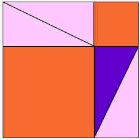 |

