„ich jedenfalls bin davon überzeugt, dass Er nicht würfeln.,“
~ Albert Einstein
- Zufallsvariablen
- Diskrete Zufallsvariablen
- Kontinuierliche Zufallsvariablen
- Gemischte Zufallsvariablen
- Kumulative Verteilungsfunktionen (CDF)
- Wahrscheinlichkeitsdichtefunktion (PDF)
- Interaktive CDF/PDF Beispiel
Zufallsvariablen:

Sagen Sie, Sie sollten eine Münze aus Ihrer Tasche nehmen und in die Luft werfen. Während es durch den Weltraum flippt, was könntest du vielleicht über seine Zukunft sagen?
Wird es heads up landen? Schwänze?, Mehr als das, wie lange wird es in der Luft bleiben? Wie oft wird es hüpfen? Wie weit von wo es zuerst auf den Boden trifft, wird es endlich zur Ruhe kommen? Wird es jemals auf den Boden fallen? Jemals zur Ruhe kommen?
Für einige solche Fragen können und werden wir uns lange vor Beobachtungen mit Antworten zufrieden geben; Wir sind ziemlich sicher, dass die Schwerkraft halten wird und die Münze landen wird. Aber für andere haben wir keine andere Wahl, als zu urteilen und vage zu sprechen, wenn wir überhaupt etwas Nützliches über die Zukunft sagen wollen.,
Als Wissenschaftler ist es natürlich unsere Aufgabe, etwas Nützliches (oder zumindest Autoritatives) zu sagen…), während die metaphorischen Münzen des physischen Systems noch in der Luft sind. Kopf oder Schwanz können sogar eine Frage von Leben oder Tod sein. Unsere Münzen können beispielsweise verschiedene mögliche Kühlmitteldurchflussraten oder Uranmassen in einem Kernkraftwerk sein. Wir wissen sehr wohl, wie groß unsere Chancen sind, dass wir statt einer Kernschmelze eine Kernschmelze bekommen.,
Für einen strengen Deterministen wurden alle diese Wetten abgeschlossen, lange bevor eine Münze, metaphorisch oder nicht, jemals geprägt wurde; wir wissen es einfach noch nicht. Wenn wir nur die Kräfte kannten, die bei einem Münzwurf ausgeübt wurden, seine genaue Verteilung der Masse, die verschiedenen winzigen Luftbewegungen im Raum… Wenn wir das alles wüssten, würden wir wissen, dass ein bestimmter Münzwurf eine 100% ige Chance hatte, so zu landen, wie er landen wird, und keine Chance auf ein anderes Ergebnis.
Aber uns fehlt natürlich oft sogar ein erwähnenswerter Bruchteil dieses Weltwissens., Darüber hinaus scheint es auf äußerst kleinen Skalen, dass strenge Deterministen absolut falsch sind; Es gibt keine Möglichkeit vorherzusagen, wann zum Beispiel ein Uranatom gespalten wird, und wenn ein solches Ereignis die größere Welt beeinflusst, dann ist dieses Makroereignis wirklich unvorhersehbar. Einige Ergebnisse sind wirklich in der Luft, verunsichert, bis sie Teil der Vergangenheit sind.
Um diese Realität zu bewältigen und die zukünftigen Zustände eines Systems sinnvoll beschreiben zu können, verwenden wir Zufallsvariablen., Eine Zufallsvariable ist einfach eine Funktion, die jedes mögliche physikalische Ergebnis eines Systems mit einer eindeutigen reellen Zahl in Beziehung setzt. Als solche gibt es drei Arten von Zufallsvariablen: diskret, kontinuierlich und gemischt. In den folgenden Abschnitten werden diese Kategorien werden kurz diskutiert und es werden Beispiele gegeben.
Diskrete Zufallsvariablen:
Betrachten Sie unseren Münzwurf erneut. Wir könnten Köpfe oder Schwänze als mögliche Ergebnisse haben. Wenn wir eine Variable x als Anzahl von Köpfen in einem einzigen Wurf definieren, könnte x möglicherweise 1 oder 0 sein, sonst nichts., Eine solche Funktion, x, wäre ein Beispiel für eine diskrete Zufallsvariable. Solche Zufallsvariablen können nur diskrete Werte annehmen. Andere Beispiele wären die möglichen Ergebnisse eines Schwangerschaftstests oder die Anzahl der Schüler in einem Klassenraum.
Kontinuierliche Zufallsvariablen:
Zurück zum Münzwurf, was wäre, wenn wir den Abstand zwischen dem Ort, an dem unsere Münze zur Ruhe kam, und dem Ort, an dem sie zuerst auf den Boden fiel, beschreiben wollten. Dieser Abstand x wäre eine kontinuierliche Zufallsvariable, da er eine unendliche Anzahl von Werten innerhalb des kontinuierlichen Bereichs reeller Zahlen annehmen könnte., Die Münze könnte 1 cm oder 1,1 cm oder 1,11 cm oder weiter und weiter reisen. Andere Beispiele für kontinuierliche Zufallsvariablen wären die Masse der Sterne in unserer Galaxie, der pH-Wert von Meerwasser oder die Verweilzeit eines Analyten in einem Gaschromatographen.
Gemischte Zufallsvariablen:
Gemischte Zufallsvariablen haben sowohl diskrete als auch kontinuierliche Komponenten. Solche Zufallsvariablen sind selten anzutreffen. Für ein mögliches Beispiel können Sie jedoch das Gewicht einer Probe messen und entscheiden, dass jedes Gewicht, das als negativer Wert gemessen wird, einen Wert von 0 erhält., Auf diese Weise hat die Zufallsvariable eine diskrete Komponente bei x = 0 und eine kontinuierliche Komponente bei x > 0.
Kumulative Verteilungsfunktionen (CDF):
Es stellt sich natürlich die Frage, wie Zufallsvariablen am besten mathematisch beschrieben (und visuell angezeigt) werden können. Für diese Aufgaben verwenden wir Wahrscheinlichkeitsdichtefunktionen (PDF) und kumulative Dichtefunktionen (CDF). Da CDFs sowohl für diskrete als auch für kontinuierliche Zufallsvariablen einfacher zu verstehen sind als PDFs, werden wir zuerst CDFs erklären.
Erwägen Sie, einen fairen 6-Seiten-Würfel zu werfen., Wir hätten eine 1: 6-Chance, einen der möglichen Werte der Zufallsvariablen zu erhalten(1, 2, 3, 4, 5, oder 6). Wenn wir diese möglichen Werte auf der x-Achse zeichnen und die Wahrscheinlichkeit darstellen, jeden bestimmten Wert, x oder einen Wert kleiner als x auf der y-Achse zu messen, haben wir den CDF der Zufallsvariablen.
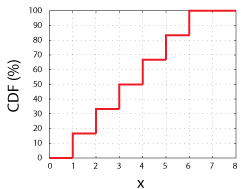
CDF für eine Messe 6-Sided Würfel. Beachten Sie, dass jeder Schritt eine Höhe von 16,67% oder 1 zu 6 hat.
Diese Funktion, CDF (x), teilt uns einfach die Wahrscheinlichkeit mit, einen beliebigen Wert bis einschließlich x zu messen., Daher müssen alle CDFs alle diese Eigenschaften haben:
- Ein CDF muss gleich 0 sein, wenn x = – ∞ ist, und sich 1 (oder 100%) nähern, wenn sich x +∞nähert. Einfach ausgedrückt, von allen möglichen Ergebnissen muss ein Ergebnis vorliegen; Die Chance, einen sechsseitigen Würfel zu werfen und einen Wert zwischen -∞ und ∞ zu erhalten, beträgt 100%.
- Die Steigung eines CDF muss immer gleich oder größer als Null sein. Betrachten Sie beispielsweise die Chance, einen 6-Seiten-Würfel zu werfen (fair oder nicht) und einen Wert zwischen 0 und 4 zu erhalten., Diese Chance kann möglicherweise nicht mehr als die Chance sein, einen Wert zwischen 0 und 5 zu erhalten, da die Chancen einer 1 -, 2-oder 3-Landung natürlich immer ein Bruchteil der Chancen sein werden, eine 1 -, 2 -, 3-oder 4-Landung zu erhalten.
Als Beispiel für eine kontinuierliche Zufallsvariable zeigt das folgende Applet die normalverteilte CDF.,div>
| -5 | 5 |
| x | |
This important distribution is discussed elsewhere., Beachten Sie einfach, dass die Eigenschaften eines CDF, die oben beschrieben und für eine diskrete Zufallsvariable erklärt wurden, auch für kontinuierliche Zufallsvariablen gelten.
Weitere intuitive Beispiele für die Eigenschaften von CDFs finden Sie im interaktiven Beispiel unten. Auch interaktive Diagramme vieler anderer CDFs, die für den Bereich Statistik wichtig sind und auf dieser Website verwendet werden, finden Sie hier.
Wahrscheinlichkeitsdichte Funktionen (PDF):
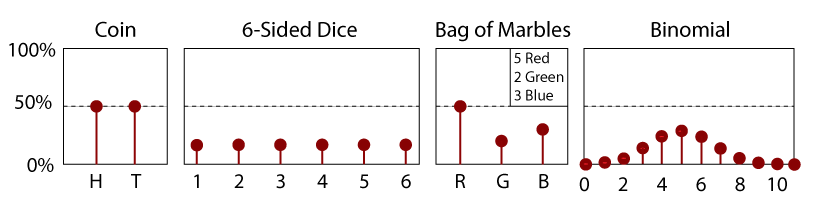
PDF für eine Messe 6-Sided Würfel.
Ein PDF ist einfach die Ableitung eines CDF., Daher ist ein PDF auch eine Funktion einer Zufallsvariablen, x, und seine Größe ist ein Hinweis auf die relative Wahrscheinlichkeit, einen bestimmten Wert zu messen. Da es sich um die Steigung eines CDF handelt, muss ein PDF immer positiv sein; Es gibt keine negativen Chancen für jedes Ereignis. Weiterhin und per Definition ist die Fläche unter der Kurve eines PDF(x) zwischen -∞ und x gleich seiner CDF(x). Daher gibt der Bereich zwischen zwei Werten x1 und x2 die Wahrscheinlichkeit an, einen Wert innerhalb dieses Bereichs zu messen.
Das folgende Applet zeigt ein PDF-Beispiel für eine normal verteilte Zufallsvariable, x.,
Normal PDF
|
x:
| mean:
| stdev:
| f(x):
|
|
Notice, when the mean and standard deviations are equal, how the PDF correlates with the normal CDF in the section above., Berücksichtigen Sie auch den Unterschied zwischen einem kontinuierlichen und einem diskreten PDF. Während ein diskretes PDF (wie das oben für Würfel gezeigte) Ihnen die Chancen gibt, ein bestimmtes Ergebnis zu erzielen, sind Wahrscheinlichkeiten mit kontinuierlichen PDFs Fragen der Reichweite, keine diskreten Punkte. Zum Beispiel gibt es eindeutig eine 1 in 6 (16.6%) Chance, eine 3 auf einem Würfel zu rollen, wie in seinem PDF zu sehen ist. Aber was sind die Chancen, genau Null mit einer Zufallsvariablen mit einem normalen PDF und einem Mittelwert von Null zu messen, wie oben gezeigt? Obwohl es der Wert ist, bei dem das PDF am größten ist, steigt die Chance, genau zu messen..,. ist, vielleicht, intuitiv, Null. Die Chancen, eine bestimmte Zufallszahl mit unendlicher Genauigkeit zu messen, sind in der Tat Null. Mit einem kontinuierlichen PDF können Sie stattdessen fragen, wie hoch die Wahrscheinlichkeit ist, dass Sie zwischen zwei Werten messen, um eine Wahrscheinlichkeit zu erhalten, die größer als Null ist. Um diese Wahrscheinlichkeit zu finden, verwenden wir einfach die CDF unserer Zufallsvariablen., Da der CDF uns die Wahrscheinlichkeit mitteilt, einen Wert oder etwas Niedrigeres als diesen Wert zu messen, um die Wahrscheinlichkeit zu ermitteln, zwischen zwei Werten zu messen, x1 und x2 (wobei x1 > x2), müssen wir einfach den Wert des CDF bei x1 nehmen und davon den Wert des CDF bei x2 subtrahieren. Wenn wir beispielsweise den normalen CDF im obigen Applet verwenden (mit μ=0 und σ=1), finden wir CDF(x=0.1)=53.9828% und CDF(x=0.2)=57.9260%, wenn wir die Messwahrscheinlichkeit zwischen 0.01 und 0.02 kennen möchten. Dann gibt uns die Differenz CDF(0.2)-CDF(0.1) die Chancen von etwa 3.9%, ein x zwischen 0.1 und 0.2 zu messen., Weitere intuitive, visuelle Beispiele für die Eigenschaften von PDFs finden Sie im interaktiven Beispiel unten. Hier können Sie auch interaktive Diagramme vieler wichtiger PDFs sehen, die auf dieser Website verwendet werden. |
|||||||||||||||||