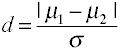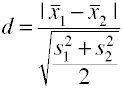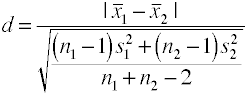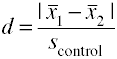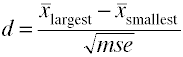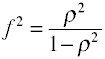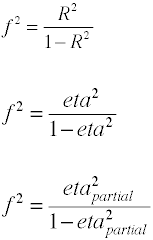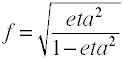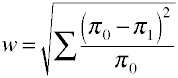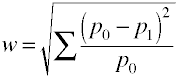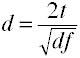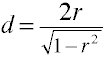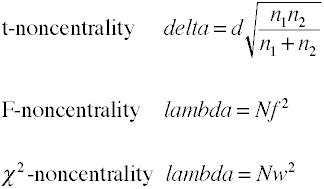un uso de effect-size es como un índice estandarizado que es independiente del tamaño de la muestra y cuantifica la magnitud de la diferencia entre las poblaciones o la relación entre las variables explicativas y de respuesta. Otro uso del tamaño del efecto es su uso en la realización de análisis de potencia.
Tamaño del efecto para la diferencia de medias
El tamaño del efecto para las diferencias de medias se da por la d de Cohen se define en términos de medias de población (µs) y una desviación estándar de población (σ), como se muestra a continuación.,
hay varias maneras diferentes que uno podría estimar σ A partir de datos de muestra que conduce a múltiples variantes dentro de la familia D de Cohen.
usando la desviación estándar cuadrada media de la raíz
usando la desviación estándar agrupada (Hedges’ g)
Esta versión de D de Cohen utiliza la desviación estándar agrupada y también se conoce como coberturas’ g.,
puede obtener fácilmente este valor de un programa anova tomando la raíz cuadrada del error meansquare, que también se conoce como error cuadrado medio raíz.
Usando la desviación estándar del grupo de control (vidrio’ Δ)
otra versión de la D de Cohen usando la desviación estándar para el grupo de control también se conoce como vidrio’ Δ.,
Más de dos grupos
Cuando hay más de dos grupos usan la diferencia entre el mayor y smallestmeans dividida por la raíz cuadrada del error cuadrático.
Tamaño del efecto para las relaciones F en el análisis de regresión
para la regresión OLS la medida del tamaño de los efectos es F, que Cohen define de la siguiente manera.,
Una vez más, hay varias formas en las que el tamaño del efecto se puede calcular a partir de datos de muestra. Nota que η2 es otro nombre para R2.
Tamaño del efecto para las relaciones F en el análisis de varianza
El tamaño del efecto utilizado en el análisis de varianza se define por la relación de variables estándar de la población.,
aunque la f de Cohen se define como la anterior, generalmente se calcula tomando la raíz cuadrada de f2.
Tamaño del efecto para χ2 desde tablas de contingencia
Una vez más comenzamos con la fórmula de definición en términos de valores de población.El tamaño del efecto w es la raíz cuadrada de la estadística estandarizada de chi-cuadrado.,
y aquí está cómo se calcula w utilizando datos de muestra.
Aquí hay una tabla de valores sugeridos para efectos bajos, medios y altos (Cohen, 1988). Estos valores no deben tomarse como absolutos y deben interpretarse en el contexto de su programa de investigación. En la práctica, los valores de los grandes efectos se superan con frecuencia con valores de Cohen D superiores a 1,0, no es infrecuente.,Sin embargo, el uso de tamaños de efecto muy grandes en el análisis prospectivo de potencia probablemente no es una buena idea, ya que podría conducir a estudios con baja potencia.,fórmulas
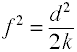
donde k = número de grupos
Convertir t a d para dos grupos independientes
Convertir r a d para dos grupos independientes
Noncentrality estimaciones
El análisis de la potencia utilizando métodos analíticos requieren una estimación de noncentrality que es basicallythe tamaño del efecto se multiplica por el tamaño de la muestra factor., Aquí hay algunas fórmulas para estimar la no centralidad.
ejemplo de análisis de potencia
Aquí hay un ejemplo que reúne el tamaño del efecto y la no centralidad en un análisis de potencia.
considere un análisis de varianza unidireccional con tres grupos (k = 3). Si esperamos que andeta2 sea igual .,12 en cuyo caso el tamaño del efecto será
effect size f = sqrt(eta2/(1-eta2)) = sqrt(.12/(1-.12)) = .369con un tamaño de muestra proyectado de 60 la estimación de no centralidad es
noncentrality coefficient lambda = N*f = 60*.369^2 = 60*.136 = 8.17el numerador grados de libertad es k-1 = 3-1 = 2 mientras que el denominador df es N-k = 60-3 = 57.El valor crítico de F con 2 y 57 grados de libertad es 3.16. Lo que resulta en una potencia de
power = noncentralFtail(df1,df2,lambda,Fcrit(2,57)) = noncentralFtail(2,57,8.17,3.16) = .703por lo tanto, un N de 60 y el tamaño del efecto de .369 produce una potencia proyectada de aproximadamente .7.
podemos mejorar el poder de .7 utilizando un tamaño de muestra proyectado de 75 en lugar de 60., Con el mismo tamaño de efecto de.369, obtenemos una nueva estimación de no centralidad de
noncentrality coefficient lambda = N*f = 75*.369^2 = 75*.136 = 10.2los grados de libertad del numerador siguen siendo los mismos mientras que el denominador df ahora es igual a N-k = 75-3 = 72.El valor crítico de F con 2 y 72 grados de libertad de 3.12. Esta vez la potencia es
power = noncentralFtail(df1,df2,lambda,Fcrit(2,72)) = noncentralFtail(2,72,10.2,3.12) = .807que está dentro de los límites de investigación aceptables.
tenga en cuenta que diferentes paquetes stat usan diferentes nombres y un orden diferente de argumentos en la función que hemos llamado noncentralFtail. Tendrá que leer la documentación que viene con su software.,
Becker, L. Psicología 590 Notas del curso. Visto el 19 de Junio de 2009 <http://web.uccs.edu/lbecker/Psy590/es.htm>
Cohen, J. 1988. Statistical power analysis for the behavioral sciences. Hillsdale, Nueva Jersey: Lawrence Erlbaum Associates