A Cox arányos veszélyek modellje

korábban írtam arról, hogyan kell kiszámítani a Kaplan–Meier görbét a túlélési adatokhoz. Nem parametrikus becslőként jó munkát végez, ha gyorsan megvizsgálja az adatkészlet túlélési görbéjét. Azonban nem engedi, hogy modellezze a kovariánsok túlélésre gyakorolt hatását. Ebben a cikkben a Cox arányos veszélyek modelljére összpontosítunk, amely a túlélési adatok egyik leggyakrabban használt modellje.

bemegyünk néhány mélységet, hogyan kell kiszámítani a becslések., Ez azért értékes, mert látni fogjuk, hogy a becslések csak a hibák megrendelésétől függenek, nem pedig a tényleges idejüktől. Röviden megvitatunk néhány trükkös kérdést az ok-okozati következtetésről, amelyek különlegesek a túlélési elemzéshez.

általában a túlélési adatokra gondolunk az alábbi túlélési görbék tekintetében.,

az X-tengelyen napok alatt van az idő. Az y-tengelyen van (egy becslés) a népességben lévő alanyok százalékos (technikailag arányos) aránya, amely “túléli” az adott időt. A túlélés lehet ábrás vagy szó szerinti., Lehet, hogy az emberek egy bizonyos életkorig élnek-e, függetlenül attól, hogy egy gép bizonyos időt tesz-e le anélkül, hogy lebontaná, vagy lehet, hogy valaki bizonyos ideig munkanélküli marad, miután elvesztette munkáját.

a túlélési elemzés komplikációja az, hogy egyes alanyok nem figyelték meg “halálukat”. Lehet, hogy még életben vannak, egy gép továbbra is működik, vagy valaki még mindig munkanélküli lehet az adatok gyűjtésének időpontjában., Az ilyen megfigyeléseket “jobb cenzúrának” nevezik, a cenzúra kezelése pedig azt jelenti, hogy a túlélési elemzéshez különböző statisztikai eszközökre van szükség.

a túlélő funkciót S-ként, az idő függvényeként jelöljük. Kimenete a T. időpontban túlélő alanyok százalékos aránya (ismét technikailag 0 és 1 közötti arány, de a két szót felváltva fogom használni). Az egyszerűség kedvéért azt a technikai feltételezést fogjuk tenni, hogy ha elég sokáig várunk, minden alany “meghal”.”

az alanyokat indexeljük egy olyan alindextel, mint i vagy j., A hiba alkalommal a teljes népesség jelenik meg egy hasonló alsó index az idő változó t.

Egy újabb finomság, hogy fontolja meg, hogy kezeljük időben, mint a diszkrét (hétről hétre, mondjuk), vagy folyamatos. Filozófiai szempontból csak diszkrét lépésekben mérjük az időt (mondjuk a legközelebbi másodpercre)., Adataink általában csak azt mondják meg nekünk, ha valaki egy adott évben meghalt, vagy ha egy gép egy adott napon meghibásodott. Oda-vissza megyek a diszkrét és folyamatos ügyek között, hogy a kiállítás a lehető legtisztább legyen.

amikor megpróbáljuk modellezni a kovariánsok (pl. életkor, nem, faj, gépgyártó) hatásait, általában érdekelni fogjuk a kovariánsnak a veszélyességi sebességre gyakorolt hatását. A veszélyességi arány a kudarc/halál/állapot átmenet pillanatnyi valószínűsége egy adott időpontban t, attól függően, hogy már túlélték-e ezt a hosszú időt., Meg fogjuk jelölni λ (t). Az idő diszkrét kezelése:

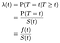
ahol f a teljes valószínűségi sűrűsége hiányában időben t. tudjuk egyesíteni a diszkrét és folyamatos esetekben lehetővé teszi Delta függvények a valószínűségi sűrűség “függvény”. Így az eredmény λ = f / S ugyanaz a folyamatos esetben.

javítsunk egy példát., Tekintsük a klinikai vizsgálat összefüggését, ahol egy gyógyszer kezdetben betegséget okoz a remisszióban. Azt fogjuk mondani, hogy a gyógyszer “kudarcot vall” egy alany számára, amikor a betegség előrehalad egy alany számára. Végül tegyük fel, hogy az alanyok betegségállapotát hetente mérik. Akkor, ha λ (3) = 0,1, ez azt jelenti, hogy 10% esély van arra, hogy egy adott alany esetében, ha a 3.hét előtt még mindig remisszióban vannak, betegségük a 3. héten kezd előrehaladni. A másik 90% remisszióban marad.,

ezután az F teljes valószínűségi sűrűségfüggvény csak az S származéka az idő tekintetében. (Ismét, ha az idő diszkrét, f csak néhány delta funkció összege).,341fa8b2″>

Ez azt jelenti, hogy ha tudjuk, hogy a Figyelmeztető funkció, meg tudjuk oldani ezt a differenciál egyenlete S:

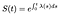
Ha az idő diszkrét, a szerves összegét a delta funkciók csak átalakul egy összeget a veszélyek minden diszkrét idő.,

Oké, ez összegzi a jelölést és az alapvető fogalmakat, amelyekre szükségünk lesz. Folytassuk a modellek megvitatását.

Non-, Semi -, és teljesen parametrikus modellek

mint korábban említettem, jellemzően a λ Veszélyességi Arány modellezése érdekli.

egy nem parametrikus modellben nem teszünk feltételezéseket a λ funkcionális formájáról. Ebben az esetben a Kaplan–Meier görbe a legnagyobb valószínűség-becslés. A hátránya az, hogy ez megnehezíti a kovariánsok bármilyen hatásának modellezését. Ez egy kicsit olyan, mint egy scatter telek használata, hogy megértsük a kovariáns hatását., Nem feltétlenül olyan hasznos, mint egy teljesen parametrikus modell, mint egy lineáris regresszió.

egy teljesen parametrikus modellben feltételezzük a λ pontos funkcionális formáját. A teljesen parametrikus modellek megvitatása önmagában egy teljes cikk,de érdemes egy nagyon rövid vitát. Az alábbi táblázat három leggyakoribb teljesen parametrikus modellt mutat be. Mindegyik általánosítható a következővel, 1-2-3 paraméterrel. A veszélyességi funkció funkcionális formája a középső oszlopban látható. A veszélyfüggvény logaritmusa az utolsó oszlopban is látható., Minden paraméter (ɣ, α, μ) pozitívnak tekinthető, kivéve, hogy μ lehet 0 az általánosított Weibull eloszlásban (a Weibull Eloszlás reprodukálása).

Nézi a logaritmusát azt mutatja, hogy az exponenciális modell feltételezi, hogy a figyelmeztető funkció állandó. A Weibull modell azt feltételezi, hogy növekszik, ha α >1, állandó, ha α=1, és csökken, ha α< 1., Az általánosított Weibull modell ugyanúgy indul, mint a Weibull modell (az elején ln s = 0). Ezután egy extra kifejezés következik.

ezekkel a modellekkel az a probléma, hogy erős feltételezéseket tesznek az adatokról. Bizonyos kontextusokban okkal feltételezhető, hogy ezek a modellek jól illeszkednek. De ezekkel, valamint számos más lehetőség áll rendelkezésre, fennáll annak a veszélye, hogy helytelen következtetéseket von le a modell hibás meghatározása miatt.

Ez az oka annak, hogy a Cox arányos veszélyek, a félig parametrikus modell annyira népszerű., A Veszélyfüggvény alakjára vonatkozóan nincsenek funkcionális feltevések; ehelyett csak a kovariánsok hatásairól tesznek funkcionális-formai feltételezéseket.,

A Cox arányos veszélyek modellje

A Cox arányos veszélyek modelljét általában a T idő, az X kovariáns vektor és a β együttható

ahol a λₒ az idő önkényes függvénye, a kiindulási veszély. Az X és β pontterméke ugyanúgy az exponensben van, mint a standard lineáris regresszióban., A kovariánsok értékétől függetlenül minden alanynak ugyanaz a kiindulási értéke λ λ. Ezt követően a kovariánsok alapján kiigazításokat végeznek.

az Eredmények Értelmezése

Hiszem, hogy abban a percben, hogy mi illik egy Cox Arányos Veszélyek a modell, hogy az adat, amely abból állt,

1. Egy oszlop meghatározza az egyes tárgy
2. Egy oszlop meghatározza, hogy a téma volt a “megfigyelt” (sikertelen volt, vagy, a kívánt példa, hogy a betegség előrehaladását). Az 1-es érték azt jelenti, hogy a beteg betegsége előrehaladt., A 0 érték azt jelenti,hogy az utolsó megfigyelési időpontban a betegség nem fejlődött ki. A megfigyelést cenzúrázták.
3. oszlopok a kovariánsokhoz X.

az illesztés után megkapjuk a β értékeket. Tegyük fel például, hogy az egyszerűség kedvéért egyetlen kovariáns van. A β = 0,1 érték azt jelenti, hogy a kovariáns 1-es mennyiségének növekedése a betegség progressziójának körülbelül 10% – os nagy esélyéhez vezet egy adott időpontban., A pontos értéket a tény,

A kis értékek, a β értéke β önmagában elég jó közelítése a pontos növeli a veszélyt. Nagyobb β értékek esetén a pontos összeget ki kell számítani.

a β=0, 1 kifejezésének másik módja az, hogy az x növekedésével a veszély 10% – kal növekszik az X 1-es növekedésénél. A nagyobb 10.,52% a (folyamatos) összetételből származik, csakúgy, mint az összetett kamat.

továbbá a β=0 nem jelent hatást, a β negatív pedig azt jelenti, hogy a kovariáns növekedésével kevesebb a kockázat. Ne feledje, hogy a szokásos regressziókkal ellentétben nincs elfogási kifejezés. Ehelyett az intercept abszorbeálódik a λ λ kiindulási veszélybe, amely szintén becsülhető (lásd alább).

végül, feltételezve, hogy megbecsültük a kiindulási veszély függvényt, meg tudjuk építeni a túlélő függvényt.,

div >

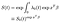
az alapfüggvény a kovariánsokból származó EXP(xʹß) faktor erejére emelkedik. Némi figyelmet kell fordítani a kiindulási túlélő függvény értelmezésére, amely nagyjából az intercept kifejezés szerepét játssza a rendszeres lineáris regresszióban. Ha a kovariánsok középpontba kerültek (átlag 0), akkor ez az “átlagos” tárgy túlélő funkcióját jelenti.,

A Cox arányos veszélyek modelljének becslése

Az 1970-es években David Cox, egy brit matematikus javasolta a β becslésének módját anélkül, hogy meg kellett volna becsülni a kiindulási veszélyt λₒ. A kiindulási veszélyt később is meg lehet becsülni. Mint korábban említettük, látni fogjuk, hogy a megfigyelt kudarcok rendezése számít, nem maguk az idők.

a becslésbe való ugrás előtt érdemes megvitatni a kapcsolatokat. Mivel általában csak diszkrét lépésekben figyeljük az adatokat, lehetséges, hogy két hiba fordulhat elő egyszerre., Például két gép meghibásodhat ugyanazon a héten, a felvétel csak heti rendszerességgel készül. Ezek a kapcsolatok meglehetősen bonyolulttá teszik a helyzet elemzését anélkül, hogy sok betekintést adnának hozzá. Következésképpen, én levezetni a becslések esetében nincs kapcsolat.

emlékezzünk arra, hogy adataink bizonyos számhibák megfigyeléseiből állnak diszkrét időben. Legyen R (t) jelöli a lakosság “veszélyeztetett” idején t. ha egy alany a vizsgálat nem sikerült (betegség előrehaladtával, például) idő előtt t, akkor nem “veszélyben.,”Továbbá, ha a tanulmányunkban szereplő alanyok megfigyelését a t idő előtti időben cenzúrázták, akkor ők sem “vannak veszélyben.”

a szokásos módon szeretnénk építeni egy valószínűségét funkció (mi a valószínűsége annak, mi lett volna a megfigyelt adatok tettünk, mivel a covariates, valamint együtthatók), majd optimalizálni, hogy a maximális-a valószínűsége becslő.

minden diszkrét időpontban, amikor megfigyeltük a J alany kudarcát, az előfordulás valószínűsége, tekintettel arra, hogy hiba történt, alacsonyabb. Az összeget a J időpontban veszélyeztetett összes alanyra átveszik.,

Figyeljük meg, hogy a kiindulási veszélyességi λₒ esett ki! Nagyon kényelmes. Ezért a valószínűség, amit építünk, csak részleges valószínűség. Vegye figyelembe azt is, hogy az idők egyáltalán nem jelennek meg., A J tárgy kifejezése csak attól függ, hogy mely alanyok még életben vannak a J időpontban, ami viszont csak attól függ, hogy az alanyokat cenzúrázzák vagy betartják-e.

a részleges valószínűség természetesen csak ezeknek a kifejezéseknek a terméke, minden egyes kudarc esetén (nincs cenzúrázott megfigyelés).,

A napló részleges valószínűsége, akkor

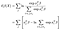
A fit történik standard numerikus módszerek, például a python csomag statsmodels a variancia-covariance mátrix a becslések által adott (inverz) Fisher Információs Mátrix. Semmi izgalmas itt.,

az alap túlélő függvény becslése

most, hogy megbecsültük az együtthatókat, meg tudjuk becsülni a túlélő függvényt. Ez végül nagyon hasonlít a Kaplan–Meier görbe becsléséhez.

az I. által indexelt α kifejezéseket posztuláljuk. az i. időpontban az alaptúlélési görbének az α frakcióval kell csökkennie, amely a veszélyeztetett alanyok arányát képviseli, amelyek az i. időpontban kudarcot vallnak., Más szavakkal

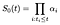
ahhoz, Hogy kiszámolja a maximum likelihood becslés α, figyelembe vesszük a valószínűsége hozzájárulás tárgyát, azt, ami nem az én külön-külön a hozzájárulást azok, hogy cenzúrázzák az idő.

A témáról, hogy nem az idő, a valószínűség által adott annak a valószínűsége, hogy élnek az alkalom, hogy kevesebb a valószínűsége, hogy életben vannak a legközelebb i+1. (Ideiglenesen feltételezzük, hogy az idők megrendelésre kerülnek).,

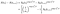
Ha ahelyett, hogy cenzúrázzák az idő, a hozzájárulás csak annak a valószínűsége, hogy élnek az idő után, azaz, hogy még nem halt meg., Ez csak

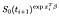
van egy extra kifejezés az alanyokat, hogy figyeltek meg (azaz megfigyelhető, hogy sikerül, ahelyett, hogy cenzúrázott)., A napló valószínűséggel válik,

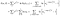
én már egy kicsit hanyag nyomon követhetőek a végpontok (én vs i+1), de minden rendbe fog jönni.

csak α kifejezések vannak a megfigyelt alanyok számára., Az α-j tekintetében megkülönböztetve, és feltételezve, hogy nincs kapcsolat, a bal oldali összegből csak a J időpontban élő alanyok számára kapunk hozzájárulást, a jobb oldali kifejezésből pedig egyetlen hozzájárulást.,qual, hogy a 0 azt jelenti, hogy meg tudjuk szerezni a maximum likelihood becslések α segítségével a becsült β, mint a megoldás a több egyenletek, egy minden témát, ami megfigyelhető volt, hogy sikerül:

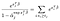
Fájlokat, illetve Kifogások

rengeteg mondanivalóm Cox Arányos Veszélyek modellek, de megpróbálom tartani a dolgokat, rövid, csak megemlíteni néhány dolgot.,

például érdemes megfontolni az időváltozós regresszorokat, és ez lehetséges.

a másik fontos dolog, amelyet szem előtt kell tartani, a változó torzítás. A standard lineáris regresszióban a regresszorokkal nem összefüggő kihagyott változók nem jelentenek nagy problémát. Ez nem igaz a túlélési elemzésben. Tegyük fel, hogy adatainkban két egyenlő méretű és mintavételezett alpopuláció van, amelyek mindegyike állandó veszélyességi rátával rendelkezik, az egyik 0,1, a másik pedig 0,5. Kezdetben magas veszélyességi arányt fogunk látni (az átlag, csak 0,3)., Az idő előrehaladtával a magas veszélyességi rátával rendelkező népesség elhagyja a lakosságot, és megfigyeljük a 0,1-re csökkenő veszélyességi rátát. Ha kihagyjuk a két populációt reprezentáló változót, az alapkockázati arányunk teljesen el lesz rontva.