Statisztikák Meghatározások > ANOVA
Tartalom:
- Az ANOVA-Teszt
- egyirányú ANOVA
- Két Way ANOVA
- Mi az a NAP?
- mi az a faktoriális ANOVA?
- hogyan kell futtatni egy ANOVA
- ANOVA vs. T teszt
- ismételt intézkedések ANOVA
- Sphericity
az ANOVA teszt
mi az az ANOVA?, Nézze meg a videót a bevezetéshez, vagy olvassa el alább:
még mindig problémái vannak? Chegg.com meg fog egyezni egy oktatóval (az első lecke ingyenes!).
az ANOVA teszt egy módja annak, hogy megtudja, a felmérés vagy a kísérlet eredményei jelentősek-e. Más szavakkal, segítenek kitalálni, hogy el kell-e utasítania a null hipotézist, vagy el kell fogadnia az alternatív hipotézist.
alapvetően csoportokat tesztel, hogy megnézze, van-e különbség közöttük., Példák arra, hogy mikor érdemes különböző csoportokat tesztelni:
- a pszichiátriai betegek egy csoportja három különböző terápiát próbál ki: tanácsadást, gyógyszeres kezelést és biofeedback-et. Látni akarja, hogy az egyik terápia jobb-e, mint a többi.
- a gyártónak két különböző folyamata van az izzók készítéséhez. Tudni akarják, hogy az egyik folyamat jobb-e, mint a másik.
- a különböző főiskolák diákjai ugyanazt a vizsgát teszik. Szeretné látni, hogy az egyik Főiskola felülmúlja-e a másikat.
mit jelent az” egyirányú “vagy a” kétirányú?,
egyirányú vagy kétirányú a független változók (IVs) számára utal a Varianciateszt elemzésében.
- az egyirányú változónak egy független változója van (2 szinttel). Például: márka gabona,
- kétirányú két független változók (ez lehet több szinten). Például: gabona márka, kalória.
mik azok a “csoportok”vagy ” szintek”?
a csoportok vagy szintek különböző csoportok ugyanazon független változón belül. A fenti példában, a szintek “márka gabona” lehet szerencsés varázsa, mazsola korpa, kukoricapehely — összesen három szinten., A “kalóriák” szintje lehet: édesített, cukrozatlan — összesen két szint.
tegyük fel, hogy tanul, ha egy alkoholos támogató csoport és egyéni tanácsadás kombinált a leghatékonyabb kezelés csökkenti az alkoholfogyasztást. A vizsgálat résztvevőit három csoportra vagy szintre oszthatja:
- csak gyógyszeres kezelés,
- gyógyszeres kezelés és tanácsadás,
- csak tanácsadás.
a függő változó a napi fogyasztott alkoholtartalmú italok száma.,
Ha a csoportok vagy szintek hierarchikus struktúrával rendelkeznek (minden szintnek egyedi alcsoportjai vannak), akkor az elemzéshez használjon beágyazott ANOVA-t.
mit jelent a” replikáció”?
Ez az, hogy Ön replikáló(azaz duplikáló) a teszt (ek) több csoport. A kétirányú ANOVA a replikáció, van két csoport és az egyének, hogy a csoport csinál több, mint egy dolog (azaz két csoport diák két főiskola vesz két teszt). Ha csak egy csoport vesz két tesztet, akkor replikáció nélkül használná.
A tesztek típusai.,
két fő típus létezik: egyirányú és kétirányú. A kétirányú tesztek replikációval vagy anélkül is elvégezhetők.
- egyirányú ANOVA csoportok között: két csoport tesztelésére használják, hogy megnézzék, van-e különbség közöttük.
- kétirányú ANOVA replikáció nélkül: akkor használatos, ha egy csoportja van, és ugyanazt a csoportot kétszer teszteli. Például, te teszteli egy sor egyének előtt és után vesznek egy gyógyszert, hogy ha működik, vagy sem.
- kétirányú ANOVA replikációval: két csoport, és ezeknek a csoportoknak a tagjai egynél több dolgot csinálnak., Például a különböző kórházakból származó betegek két csoportja két különböző terápiát próbál.
vissza a tetejére
egyirányú ANOVA
egyirányú ANOVA két eszköz összehasonlítására szolgál két független (független) csoportból az F-eloszlás használatával. A teszt nullhipotézise az, hogy a két eszköz egyenlő. Ezért egy jelentős eredmény azt jelenti, hogy a két eszköz egyenlőtlen.
példák arra, hogy mikor kell használni egyirányú ANOVA
1. helyzet: van egy csoport egyének véletlenszerűen kisebb csoportokra oszlik, és különböző feladatokat., Például, lehet, hogy tanulmányozza a hatását tea fogyás alkotnak három csoport: zöld tea, fekete tea, nincs tea.
2. helyzet: hasonló az 1. helyzethez, de ebben az esetben az egyéneket csoportokra osztják az általuk birtokolt attribútum alapján. Például, lehet, hogy tanulmányozza a láb erejét az emberek szerint súly. A résztvevőket súlykategóriákra (elhízott, túlsúlyos és normális) oszthatjuk, és egy súlygépen mérhetjük a lábszár erejét.,
az ANOVA
egyirányú korlátozása az ANOVA azt fogja mondani, hogy legalább két csoport különbözött egymástól. De nem fogja megmondani, hogy melyik csoport különbözött. Ha a teszt jelentős f-statisztikát ad vissza, előfordulhat, hogy ad hoc tesztet kell futtatnia (mint például a legkevésbé jelentős Különbségteszt), hogy pontosan megmondja, mely csoportoknak volt különbség az eszközökben.
vissza a tetejére
kétirányú ANOVA
a kétirányú ANOVA az egyirányú ANOVA kiterjesztése. Egy módon, van egy független változó érintő függő változó., Kétirányú ANOVÁVAL két független van. Használjon kétirányú ANOVA-t, ha van egy mérési változó (azaz kvantitatív változó) és két névleges változó. Más szóval, ha a kísérletnek kvantitatív eredménye van, és két kategorikus magyarázó változója van, akkor az ANOVA kétféleképpen megfelelő.
például érdemes lehet megtudni, hogy van-e interakció a jövedelem és a nem között a szorongás szintjén az állásinterjúk során. A szorongási szint az eredmény, vagy a mérhető változó. A nemek és a jövedelem a két kategorikus változó., Ezek a kategorikus változók a független változók is, amelyeket két módon ANOVA tényezőknek neveznek.
a tényezők szintekre oszthatók. A fenti példában a jövedelmi szint három szintre osztható: alacsony, közepes és magas jövedelemre. A nem három szintre osztható: férfi, nő és transznemű. A kezelési csoportok a tényezők összes lehetséges kombinációja. Ebben a példában 3 x 3 = 9 kezelési csoport lenne.
fő hatás és interakciós hatás
a kétirányú ANOVA eredményei kiszámítják a fő hatást és az interakciós hatást., A fő hatás hasonló egyirányú ANOVA-hoz: minden tényező hatását külön kell figyelembe venni. Az interakciós hatással minden tényezőt egyszerre kell figyelembe venni. A tényezők közötti interakciós hatásokat könnyebb tesztelni, ha minden sejtben egynél több megfigyelés van. A fenti példában több stressz pontszámokat lehet beírni a sejtekbe. Ha több megfigyelést ír be a cellákba, akkor az egyes cellák számának egyenlőnek kell lennie.
két null hipotézist tesztelnek, ha egy megfigyelést helyez el minden cellában., Ebben a példában ezek a hipotézisek a következők:
H01:minden jövedelemcsoportnak egyenlő az átlagos stressz.
H02: minden nemi csoport egyenlő átlagos stresszel rendelkezik.
a sejtekben végzett többszörös megfigyelések esetén egy harmadik hipotézist is tesztelne:
H03: a tényezők függetlenek, vagy az interakciós hatás nem létezik.
egy F-statisztikát számítunk ki minden egyes vizsgált hipotézisre.
feltételezések kétirányú ANOVA
- a populációnak közel kell lennie a normál eloszláshoz.
- a mintáknak függetleneknek kell lenniük.
- A populációs eltéréseknek egyenlőnek kell lenniük.,
- a csoportoknak egyenlő mintamérettel kell rendelkezniük.
vissza a tetejére
mi az a MANOVA?
MANOVA csak egy ANOVA, több függő változóval. Ez hasonló a sok más vizsgálatok, kísérletek, hogy ez a célja, hogy megtudja, ha a válasz változó (azaz a függő változó) változik manipulálásával a független változó. A teszt segít számos kutatási kérdés megválaszolásában, beleértve:
- a független változók változásai statisztikailag szignifikáns hatással vannak a függő változókra?
- milyen kölcsönhatások vannak a függő változók között?,
- milyen kölcsönhatások vannak a független változók között?
Manova példa
tegyük fel, hogy meg akarta tudni, hogy a tankönyvek különbsége befolyásolta-e a diákok matematikai és tudományos pontszámait. A matematika és a tudomány fejlődése azt jelenti, hogy két függő változó létezik, tehát egy MANOVA megfelelő.
az ANOVA egyetlen (univariate) f-értéket ad, míg a MANOVA többváltozós F értéket ad. MANOVA teszteli a többszörös függő változókat új, mesterséges, függő változók létrehozásával, amelyek maximalizálják a csoportkülönbségeket., Ezek az új függő változók a mért függő változók lineáris kombinációi.
A MANOVA eredmények értelmezése
Ha a többváltozós F érték azt jelzi, hogy a teszt statisztikailag szignifikáns, ez azt jelenti, hogy valami jelentős. A fenti példában nem tudná, hogy a matematikai pontszámok javultak-e, a tudományos pontszámok javultak-e (vagy mindkettő)., Miután jelentős eredményt ért el, akkor meg kell vizsgálnia az egyes komponenseket (az univariate F teszteket), hogy megnézze, melyik függő változó(k) járultak hozzá a statisztikailag szignifikáns eredményhez.
A MANOVA vs. ANOVA előnyei és hátrányai
előnyök
- MANOVA lehetővé teszi több függő változó tesztelését.
- MANOVA védelmet nyújt az I. típusú hibák ellen.
- MANOVA sokszor bonyolultabb, mint az ANOVA, így kihívást jelent látni, hogy mely független változók befolyásolják a függő változókat.,
- a szabadság egy foka elveszik minden új változó hozzáadásával.
- a függő változókat a lehető legnagyobb mértékben össze kell kapcsolni. Ha korrelálnak, a szabadságfok elvesztése azt jelenti, hogy nincs sok előnye annak, ha egynél több függő változót is beveszünk a tesztbe.
referencia:
(SFSU)
vissza a tetejére
mi az a faktoriális ANOVA?
a faktoriális ANOVA a Varianciavizsgálat elemzése egynél több Független változóval vagy”tényezővel”. A független változó több szintjére is utalhat., Például egy kezelési csoporttal és egy kontrollcsoporttal végzett kísérletnek van egy tényezője (a kezelés), de két szintje (a kezelés és a kontroll). A “kétirányú” és a “háromirányú” kifejezések a tesztben szereplő tényezők számára vagy szintek számára utalnak. A négyutas ANOVA-t ritkán használják, mert a teszt eredményei összetettek és nehezen értelmezhetők.
- a kétirányú ANOVA két tényezővel (független változókkal) és egy függő változóval rendelkezik. Például a tanulással töltött idő és az előzetes tudás olyan tényezők, amelyek befolyásolják, hogy milyen jól teljesítesz egy teszten.,
- egy háromutas ANOVA három tényezővel (független változókkal) és egy függő változóval rendelkezik. Például a tanulással töltött idő, az előzetes tudás és az alvási órák olyan tényezők, amelyek befolyásolják, hogy mennyire jól teljesít egy teszten
Factorial ANOVA hatékony módja a teszt elvégzésének. Ahelyett, hogy egy kísérletsorozatot végezne, ahol egy független változót tesztel egy függő változóval szemben, egyszerre tesztelheti az összes független változót.
variabilitás
egyirányú ANOVA esetén a variabilitás a csoportok közötti különbségeknek és a csoportokon belüli különbségeknek köszönhető., A faktoriális ANOVA-ban minden szint és tényező párosul egymással (“keresztezett”). Ez segít látni, hogy milyen kölcsönhatások zajlanak a szintek és a tényezők között. Ha van interakció, akkor az egyik tényező különbségei a másik különbségeitől függenek.
tegyük fel, hogy kétirányú ANOVA-t futtatott, hogy tesztelje a férfi/női teljesítményt egy záróvizsgán. Az alanyok vagy 4, 6 vagy 8 órát aludtak.,
- IV1: Nem (Férfi / Nő)
- IV2: alvás (4/6/8)
- DV: záróvizsga pontszám
egy kétirányú faktoriális ANOVA segítene a következő kérdések megválaszolásában:
- a szex a fő hatás? Más szóval, a férfiak és a nők jelentősen különböznek a vizsga teljesítményétől?
- az alvás a fő hatás? Más szóval, azok az emberek, akik 4,6 vagy 8 órás alvással rendelkeztek, jelentősen különböznek teljesítményükben?
- van-e jelentős kölcsönhatás a tényezők között? Más szóval, hogyan működik óra alvás, szex kölcsönhatásba tekintetében vizsga teljesítményét?,
- lehet-e bármilyen különbség a szex és a vizsga teljesítményében az alvás különböző szintjein?
Factorial ANOVA
- normalitás: a függő változó általában eloszlik.
- függetlenség: a megfigyelések és csoportok egymástól függetlenek.
- variancia egyenlősége: a populációs varianciák egyenlőek a tényezők/szintek között.
ANOVA
futtatása ezek a tesztek kézzel nagyon időigényesek. Szinte minden esetben használni szeretné a szoftvert., Például több lehetőség áll rendelkezésre az Excelben:
- kétirányú Anova Excelben replikációval, replikáció nélkül.
- egyirányú Anova az Excel 2013-ban.
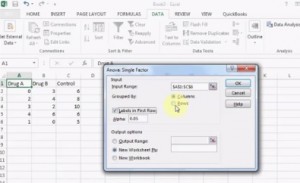
a teszt futtatása Excelben.
az ANOVA tesztek statisztikai csomagokban parametrikus adatokon futnak. Ha rangsorolt vagy megrendelt adatai vannak, akkor nem parametrikus ANOVA-t szeretne futtatni (általában a szoftver másik címe alatt található, mint például a “nem paraméteres tesztek”).,
lépések
nem valószínű, hogy kézzel szeretné elvégezni ezt a tesztet, de ha szükséges, ezek a lépések, amelyeket meg kell tennie:
- keresse meg az egyes csoportok átlagát.
- keresse meg az Általános átlagot (a csoportok átlaga együtt).
- keresse meg a csoporton belüli variációt;az egyes tagok pontszámának teljes eltérése a csoport átlagától.
- keresse meg a csoport közötti variációt:az egyes csoportok eltérése az Általános átlagtól.
- keresse meg az F statisztikát: a Csoportváltozatok közötti arány a Csoportváltozaton belül.
ANOVA vs., T teszt
a hallgató t-tesztje megmondja, hogy van-e jelentős eltérés a csoportok között. A T-teszt összehasonlítja az eszközöket, míg az ANOVA összehasonlítja a populációk közötti eltéréseket.
akkor technikailag végre egy sor T-tesztek az adatokat. Azonban, ahogy a csoportok száma növekszik, akkor a végén egy csomó pár összehasonlítást, hogy meg kell futtatni. Az ANOVA egyetlen számot (az f-statisztikát) és egy p-értéket ad a null-hipotézis támogatásához vagy elutasításához.,
vissza a tetejére
ismételt intézkedések ANOVA
ismételt intézkedések az ANOVA majdnem ugyanaz, mint az egyirányú ANOVA, egy fő különbséggel: a kapcsolódó csoportokat teszteli, nem pedig függetleneket. Ezt ismételt intézkedéseknek hívják, mert ugyanazt a résztvevőcsoportot újra és újra mérik. Például az étrend megváltoztatása után 1, 3 vagy 6 hónappal tanulmányozhatja ugyanazon betegcsoport koleszterinszintjét. Ebben a példában a független változó az “idő”, a függő változó pedig a “koleszterin”.,”A független változót általában az alanyokon belüli tényezőnek nevezik.
ismételt intézkedések az ANOVA hasonló egy egyszerű többváltozós kialakításhoz. Mindkét tesztben ugyanazokat a résztvevőket mérik újra és újra. Ismételt mérésekkel azonban ugyanazt a jellemzőt más állapotban mérik. Például a vérnyomást az “idő”állapot alatt mérik. Az egyszerű többváltozós kialakításhoz ez a jellemző változik. Például, meg tudná mérni a vérnyomást, pulzusszám és a légzési sebesség idővel.,
ismételt intézkedések alkalmazásának okai ANOVA
- ha ugyanazon résztvevőktől adatokat gyűjt egy idő alatt, az egyéni különbségek (a csoportkülönbségek forrása) csökkennek vagy megszűnnek.
- a tesztelés erősebb, mivel a minta mérete nem oszlik meg csoportok között.
- a teszt gazdaságos lehet, mivel ugyanazokat a résztvevőket használja.,
ismételt mérésekre vonatkozó feltételezések ANOVA
az ismételt mérésekből származó eredmények az ANOVA csak akkor érvényesek, ha a következő feltételezéseket nem sértették meg:
- egy független változónak és egy függő változónak kell lennie.
- a függő változónak folyamatos változónak kell lennie, intervallumskálán vagy arányskálán.
- a független változónak kategorikusnak kell lennie, akár a névleges skálán, akár a sorskálán.
- ideális esetben a csoportok párjai közötti függőség szintje egyenlő (“sphericity”)., Korrekciók lehetségesek, ha ezt a feltételezést megsértik.
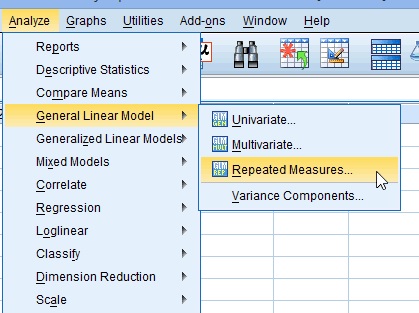
ismételt intézkedések ANOVA az SPSS-ben: lépések
1.lépés: Kattintson az “Elemzés” gombra, majd vigye az egérmutatót az “általános lineáris modell” fölé.”Kattintson” Ismételt Intézkedések.”
2.lépés: cserélje ki a” factor1 ” nevet valamire, amely a független változót képviseli. Például “kor” vagy “idő” lehet.”
3. lépés: Írja be a ” szintek számát.”Ez az, hogy hányszor mértük a függő változót. Például, ha hetente összesen 4 héten végzett méréseket, ez a szám 4 lenne.,
4. lépés: Kattintson a” Hozzáadás ” gombra, majd adjon nevet a függő változónak.
5. lépés: Kattintson a” Hozzáadás ” gombra. Egy ismételt intézkedések határozzák doboz jelenik meg. Kattintson a” meghatározás ” gombra.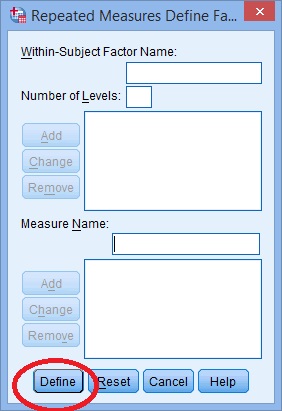
6.lépés: a nyílgombokkal mozgassa a változókat balról jobbra úgy, hogy a képernyő hasonló legyen az alábbi képhez: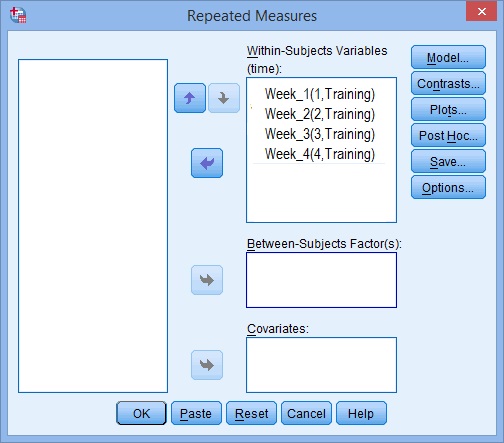
7. lépés: Kattintson a “telkek” gombra, és használja a nyilakat a tényező átviteléhez a vízszintes tengely dobozból.
8. lépés: Kattintson a “Hozzáadás” gombra, majd az ablak alján kattintson a “Folytatás” gombra.,
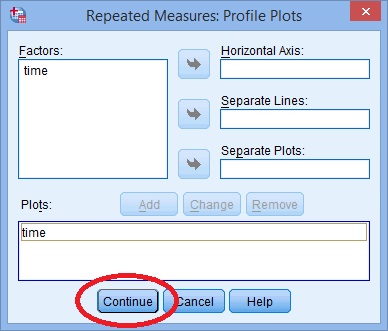
9.lépés: Kattintson az” Opciók ” gombra, majd vigye át a tényezőket a bal oldali dobozból a jobb oldali doboz megjelenítési eszközeire.
10. lépés: Kattintson a következő jelölőnégyzetekre:
- főbb hatások összehasonlítása.
- Leíró statisztika.
- a hatás méretének becslése.
11. lépés: Válassza a” Bonferroni ” lehetőséget a legördülő menüből a konfidencia intervallum beállítása alatt.
12. lépés: Kattintson a “Folytatás” gombra, majd kattintson az “OK” gombra a teszt futtatásához.,
vissza a tetejére
Sphericity
a statisztikában a sphericity (ε) a Mauchly sphericity tesztjére utal, amelyet 1940-ben John W. Mauchly fejlesztett ki, aki együtt fejlesztette ki az első általános célú elektronikus számítógépet.
definíció
Sphericity használják feltételezésként ismételt intézkedések ANOVA. A feltételezés azt állítja, hogy az összes lehetséges csoportpár közötti különbségek egyenlőek. Ha adatai megsértik ezt a feltételezést, az I. típusú hiba növekedését eredményezheti (a null hipotézis helytelen elutasítása).,
nagyon gyakori, hogy az ismételt intézkedések ANOVA a feltételezés megsértését eredményezik. Ha a feltételezést megsértették, javításokat fejlesztettek ki, amelyek elkerülhetik az I. típusú hibaarány növekedését. A korrekciót az F-eloszlás szabadságának fokára alkalmazzák.
Mauchly Sphericity tesztje
Mauchly sphericity tesztje a statisztikai szoftverek többségében futtatható, ahol általában a sphericity alapértelmezett tesztje. Mauchly tesztje ideális közepes méretű mintákhoz., Előfordulhat, hogy a kis mintákban nem érzékeli a gömböt, és nagy mintákban túlzottan kimutathatja.
Ha a teszt egy kis p-értéket ad vissza(p≤.05), ez azt jelzi, hogy adatai megsértették a feltételezést. A következő kép SPSS kimenet ANOVA azt mutatja, hogy a jelentősége “sig” csatolt Mauchly van .274. Ez azt jelenti, hogy ezt az adatkészletet nem sértették meg.
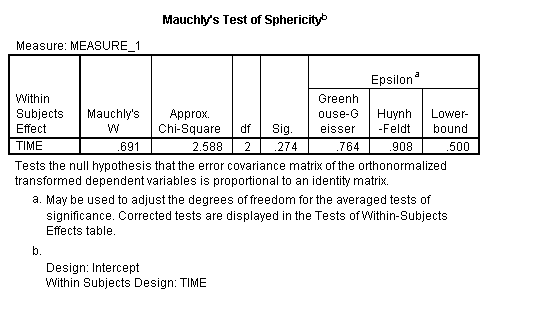
kép: UVM.,EDU
jelentené a fenti eredményt, mivel ” Mauchly tesztje azt jelezte, hogy a szfericitás feltételezését nem sértették meg, χ2(2) = 2, 588, p = .274.”
Ha a teszt egy kis p-értéket adott vissza, akkor korrekciót kell alkalmazni, általában a:
- Greehouse-Geisser korrekciót.
- Huynh-Feldt korrekció.
Ha ε ≤ 0,75 (vagy nem tudja, mi a statisztika értéke), használja az üvegházhatást okozó Geisser korrekciót.
amikor ε >.75, használja a Huynh-Feldt korrekciót.,
vissza a tetejére
Grand mean
ANOVA vs regresszió
——————————————————————————
segítségre van szüksége egy házi feladathoz vagy tesztkérdéshez? A Chegg tanulmány segítségével lépésről-lépésre megoldásokat kaphat kérdéseire a terület szakértőjétől. Az első 30 perc egy Chegg oktatóval ingyenes!