az egész számok szorzását és megosztását szabályozó szabályok nagyon hasonlóak. Ebben a leckében az egész számok szorzására összpontosítunk.
szabályok Az egész számok szorzására
1. lépés: szorozzuk meg abszolút értékeiket.
2. lépés: Határozza meg a végső válasz jelét (ebben az esetben a terméknek nevezzük, mert megszorozzuk) a következő feltételek mellett.
- 1. állapot: ha a két szám jelei azonosak, a termék mindig pozitív szám.,
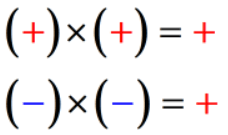
- 2.feltétel: ha a két szám jelei eltérőek, a termék mindig negatív szám.
példák egész szorzásra
1.példa: szorozzuk meg az alábbi egészeket.
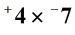
megoldás: először szerezd meg az egyes számok abszolút értékét.,
ezután szorozza meg vagy keresse meg az abszolút értékek szorzatát.
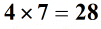
végül határozza meg a végső válasz jelét. A szabály kimondja, hogy ha a két egész szám jelei eltérőek, akkor a végső válasz negatív lesz.
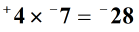
2.példa: szorozzuk meg az alábbi egészeket.,
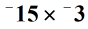
megoldás: szorozzuk meg a két szám abszolút értékeit.
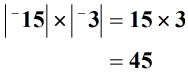
mivel ugyanazt a jelet megszorozzuk, a végső válasznak (terméknek) pozitívnak kell lennie.
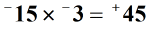
3.példa: keresse meg az alábbi három egész szám termékét.,
megoldás: három vagy több egész számot is megszorozhatunk. Egyszerre csak két egész számot kell megszoroznunk. Hadd tegyek egy zárójelet, hogy megmutassam, melyik két számot fogjuk először megszorozni. A +3 és -8 szorzata − 24. Negatív, mert a jelek eltérőek. Ezután szorozzuk meg – 24-et -2-vel, hogy +48-at kapjunk. Ne feledje, hogy két azonos jelű egész szám terméke mindig pozitív.,
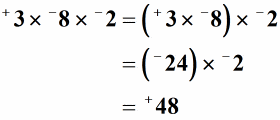
gyakorlat a munkalapokkal
is érdekelhet:
egész kiegészítés
egész kivonás
integer Division