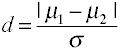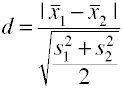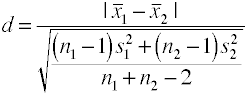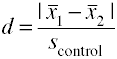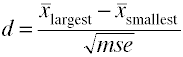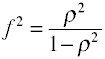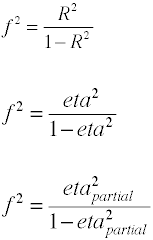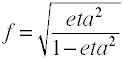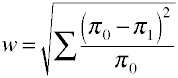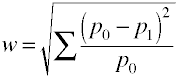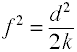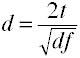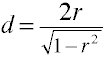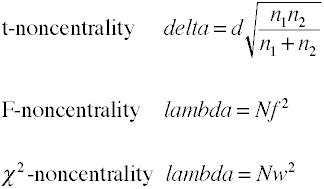az effekt-méret egyik használata standardizált index, amely független a minta méretétől, és számszerűsíti a populációk közötti különbség nagyságát vagy a magyarázó és válaszváltozók közötti kapcsolatot. A hatásméret másik használata a végrehajtásbanteljesítményelemzés.
Effect size for difference in means
Effect size for differences in means is given byCohen ‘ S d is defined in terms of population means (µs) and a population standarddeviation (σ), as lentow.,
többféle módon lehet megbecsülni a σ-t a Cohen d-családjában több variánshoz vezető mintaadatokból.
A root mean négyzet szórás
az összevont szórás (Hedges’ g)
A Cohen d > ezen verzióját használja az összevont szórás és más néven sövény “g”.,
ezt az értéket könnyen megszerezheti egy anova programból a meansquare-hiba négyzetgyökének felvételével, amely szintén gyökér átlagos négyzet hiba.
a kontrollcsoport szórása (üveg’ Δ)
egy másik változata Cohen d a standard eltérés a kontroll csoport is ismert, mint glass ‘ Δ.,
több, mint két csoport
Ha több, akkor két csoport használja a különbséget a legnagyobb és a legkisebbaz átlagos négyzet hiba négyzetgyökével osztva.
effect size for F-raties in regressziós analízis
LS regresszió esetében az effektek mérete F, amelyet Cohen a következőképpen határoz meg.,
ismét számos módja van annak, hogy a hatás mérete lehet számítani a minta adatait. Megjegyzés: η2 az R2 másik neve.
Effect size for F-rations in analysis of variancia
a variancia elemzéséhez használt hatásméretet a populációs standarddeviations aránya határozza meg.,
bár Cohen f-jét a fentiek szerint definiálják, általában az f2 négyzetgyökét veszik figyelembe.
a Hatás méret χ2 a kontingencia táblázatok
ismét elindul a definitional képlet szempontjából népesség-értékek.A W hatásméret a szabványosított chi-négyzet statisztika négyzetgyöke.,
és itt van, hogyan számítják ki a w-t a mintaadatok alapján.
itt található az alacsony, közepes és magas hatások javasolt értékeinek táblázata (Cohen, 1988). Ezeket az értékeket nem szabad abszolútnak tekinteni, és a kutatási program keretében kell értelmezni. A gyakorlatban gyakran túllépik az 1,0-nél nagyobb d értékeket, nem ritka.,Azonban a prospektív teljesítményelemzésben nagyon nagy hatásméretek alkalmazása valószínűleg nem jó ötlet, mivel az alulteljesítéses vizsgálatokhoz vezethet.,a képletek
ahol k = csoportok száma
Convert t d a két, egymástól független csoportok
Convert r d a két, egymástól független csoportok
Noncentrality becslések
Teljesítmény elemzés segítségével analitikus módszereket igényelnek becslést noncentrality ami basicallythe hatás mérete szorozva a minta mérete tényező., Íme néhány képlet a nemcentralitás becsléséhez.
example power analysis
itt van egy példa, amely egyesíti a hatás méretét és a nemcentralitást egy teljesítményelemzésben.
fontolja meg a variancia egyirányú elemzését három csoporttal (k = 3). Ha azt várjuk, andeta2 egyenlő .,12 ebben az esetben a hatás mérete
effect size f = sqrt(eta2/(1-eta2)) = sqrt(.12/(1-.12)) = .369
60-as vetített mintamérettel a nemcentralitás becslése
noncentrality coefficient lambda = N*f = 60*.369^2 = 60*.136 = 8.17
a számláló szabadsági foka k-1 = 3-1 = 2, míg a df nevező N-k = 60-3 = 57.Az F kritikus értéke 2 és 57 fokos szabadsággal 3,16. Ami a
power = noncentralFtail(df1,df2,lambda,Fcrit(2,57)) = noncentralFtail(2,57,8.17,3.16) = .703
erejét eredményezi, tehát egy 60-as n és az effekt mérete .369 hozamok a tervezett teljesítmény körülbelül.7.
mi lehet javítani a hatalom .7 A vetített minta mérete 75 helyett 60., Az azonos hatású mérete.369, kapunk egy új noncentrality becslés
noncentrality coefficient lambda = N*f = 75*.369^2 = 75*.136 = 10.2
a számláló szabadságfok ugyanaz marad, míg a nevező df most egyenlő N-k = 75-3 = 72.Az F kritikus értéke 2 és 72 fokos szabadsággal 3,12. Ezúttal a teljesítmény
power = noncentralFtail(df1,df2,lambda,Fcrit(2,72)) = noncentralFtail(2,72,10.2,3.12) = .807
, amely elfogadható kutatási határokon belül van.
kérjük, vegye figyelembe,hogy a különböző stat csomagok különböző neveket és argumentumok sorrendjét használjákaz általunk nem centralftail-nek nevezett függvény. El kell olvasnia a dokumentációtjön a szoftverével.,
Becker, L. Psychology 590 course notes. Megtekintve 19 június 2009 <http://web.uccs.edu/lbecker/Psy590/es.htm>
Cohen, J. 1988. Statisztikai teljesítményelemzés a viselkedési tudományok számára. Hillsdale, New Jersey:Lawrence Erlbaum Associates