az α-együttható a legszélesebb körben alkalmazott eljárás az alkalmazott kutatások megbízhatóságának becslésére. Amint azt Sijtsma (2009) kijelentette, népszerűsége olyan, hogy Cronbachot (1951) hivatkozásként gyakrabban említik, mint a DNS kettős spirál felfedezéséről szóló cikket., Ennek ellenére korlátai jól ismertek (Lord and Novick, 1968; Cortina, 1993; Yang and Green, 2011), ezek közül a legfontosabbak a nem összefüggő hibák, a tau-egyenértékűség és a normalitás feltételezései.
az a feltételezés, A szabálytalan alakzat hiba (a hiba pontszám pár tételek szabálytalan alakzat) az a hipotézis, hogy a Klasszikus Teszt Elmélet (Lord, s Novick, 1968), megsértése, amely arra utalhat, hogy a jelenléte összetett, többdimenziós struktúrák igénylő becslési eljárások, amelyek ezt a komplexitás figyelembe (pl., Tarkkonen, valamint Vehkalahti, 2005; Zöld-Yang, 2015)., Fontos, hogy megszüntessük azt a téves hiedelmet, hogy az α-együttható jó mutatója az unidimenzionalitásnak, mert értéke magasabb lenne, ha a skála egydimenziós lenne. Valójában éppen az ellenkezője a helyzet, amint azt a Sijtsma (2009) is kimutatta, és alkalmazása ilyen körülmények között a megbízhatóság erősen túlbecsüléséhez vezethet (Raykov, 2001). Következésképpen az α kiszámítása előtt ellenőrizni kell, hogy az adatok egydimenziós modellekhez illeszkednek-e.
a tau-egyenértékűség feltételezése (azaz,, ugyanaz a valós pontszám az összes tesztelemre, vagy egyenlő tényezőterhelés az összes elem egy faktoriális modellben) követelmény, hogy az α egyenértékű legyen a megbízhatósági együtthatóval (Cronbach, 1951). Ha megsértik a tau-egyenértékűség feltételezését, akkor a valódi megbízhatósági értéket alábecsülik (Raykov, 1997; Graham, 2006) egy olyan összeggel, amely a jogsértés súlyától függően 0,6-11,1% között változhat (Green and Yang, 2009a). Az e feltételezésnek megfelelő adatokkal való munka a gyakorlatban általában nem életképes (Teo and Fan, 2013); a kongener modell (azaz,, különböző tényező terhelések) a reálisabb.
a többváltozós normalitás követelménye kevésbé ismert, és befolyásolja mind a puntuális megbízhatósági becslést, mind a konfidencia intervallumok megállapításának lehetőségét (Dunn et al., 2014). Sheng and Sheng (2012) nemrégiben megfigyelte, hogy amikor az eloszlások ferdék és/vagy leptokurtikusak, negatív torzítás keletkezik az α együttható kiszámításakor; hasonló eredményeket mutatott be a Green and Yang (2009b) a nem normális eloszlások hatásainak elemzésében a megbízhatóság becslésében., A ferde problémák tanulmányozása sokkal fontosabb, ha látjuk, hogy a gyakorlatban a kutatók szokásosan ferde mérlegekkel dolgoznak (Miceri, 1989; Norton et al., 2013; Ho and Yu, 2014). Például Miceri (1989) becslése szerint a képesség körülbelül 2/3-a, a pszichometriai intézkedések több mint 4/5-e legalább mérsékelt aszimmetriát mutatott (azaz 1 körüli ferde). Ennek ellenére a nyárs megbízhatósági becslésre gyakorolt hatását kevéssé tanulmányozták.,
figyelembe véve az α-együttható korlátairól és torzításairól szóló bőséges szakirodalmat (Revelle and Zinbarg, 2009; Sijtsma, 2009, 2012; Cho and Kim, 2015; Sijtsma and van der Ark, 2015), felmerül a kérdés, hogy a kutatók miért használják tovább az α-t, amikor alternatív együtthatók léteznek, amelyek leküzdik ezeket a korlátokat. Lehetséges, hogy a múlt században kifejlesztett megbízhatóság becslésére szolgáló eljárások feleslegessége elősegítette a vitát. Ezt tovább súlyosbította volna az együttható kiszámításának egyszerűsége és a kereskedelmi szoftverekben való elérhetősége.,
a pxx megbízhatósági együtthatójának becslésének nehézsége a definíciójában található pxx’=σt2∕σx2, amely magában foglalja a variancia számlálóban a valódi pontszámot, ha ez természeténél fogva nem észlelhető. Az α-együttható megpróbálja közelíteni ezt a megfigyelhető eltérést az elemek vagy komponensek közötti kovarianciától. Cronbach (1951) kimutatta, hogy Tau-egyenértékűség hiányában az α-együttható (vagy Guttman lambda 3, amely egyenértékű az α-val) jó alacsonyabb kötési közelítés volt., Így, amikor a feltételezések megsértik a probléma fordítja megtalálni a lehető legjobb alsó határ; sőt ezt a nevet adják a Legnagyobb Alsó korlát módszer (GLB), amely a lehető legjobb közelítés egy elméleti szög (Jackson Agunwamba, 1977; Woodhouse-Jackson, 1977; Shapiro tíz Berge, 2000; Sočan, 2000; ten Berge, valamint Sočan, 2004; Sijtsma, 2009). Revelle and Zinbarg (2009) azonban úgy véli, hogy ω jobb alsó kötést ad, mint a GLB., Ezért van egy megoldatlan vita arról, hogy e két módszer közül melyik adja a legjobb alsó határt; továbbá a nem normalitás kérdését nem vizsgálták kimerítően, amint azt a jelen munka tárgyalja.
ω együtthatók
McDonald (1999) egy faktoriális elemzési keretrendszer megbízhatóságának becslésére javasolta a WT-együtthatót, amely formálisan kifejezhető:
ahol λj a J elem betöltése, λj2 a J elem közössége, és megegyezik a ψ egyediségével., A wt együttható, beleértve a lambdas a képletek, alkalmas mindkét amikor tau-egyenértékűségének (azaz, egyenlő tényező kirakodás az összes vizsgált tételek) létezik (wt egybe matematikailag a α), amikor az elemek különböző megkülönböztetések vannak jelen a képviselet a konstrukció (azaz más tényező kirakodás tételek: congeneric mérések). Következésképpen a wt korrigálja az α alulbecslési torzítását, amikor megsértik a tau-egyenértékűség feltételezését (Dunn et al., 2014) és különböző tanulmányok azt mutatják, hogy ez az egyik legjobb alternatíva a megbízhatóság becsléséhez (Zinbarg et al.,, 2005, 2006; Revelle and Zinbarg, 2009), bár a mai napig nem ismert a nyársas körülmények között való működése.
Ha a korrelációs között fennáll a hibák, vagy több, mint egy látens dimenzió az adatok, a hozzájárulás minden dimenzió a teljes megmagyarázott variancia becsült, megszerzése az ún. hierarchikus ω (wh), amely lehetővé teszi számunkra, hogy helyes a legrosszabb túlzó elfogultság α a többdimenziós adatok (lásd Tarkkonen, valamint Vehkalahti, 2005; Zinbarg et al., 2005; Revelle és Zinbarg, 2009)., A WT és WT együtthatók egyenértékűek egydimenziós adatokban, ezért ezt az együtthatót egyszerűen ω-nak nevezzük.
Greatest Lower Bound (GLB)
Sijtsma (2009) egy tanulmánysorozatban azt mutatja, hogy a megbízhatóság egyik legerősebb becslőjét Woodhouse és Jackson (1977) a klasszikus Tesztelmélet (CX = Ct + Ce) feltételezéseiből—egy tételközi kovariancia mátrix a megfigyelt pontszámokhoz Cx. Két részre bomlik: az elemek közötti kovarianciamátrix összege a tétel valódi pontszámaihoz Ct; valamint az elemek közötti hiba covariance mátrix Ce (ten Berge and Sočan, 2004)., Kifejezése:
ahol σx2 a vizsgálati variancia és tr(Ce) az elemek közötti kovarianciamátrix nyomára utal, amelyet olyan nehéz megbecsülni. Az egyik megoldás az volt, hogy faktoriális eljárások, mint például a minimális Rang faktor elemzés (eljárás ismert glb.F). Újabban a GLB algebrai (GLBa) eljárást Andreas Moltner (Moltner and Revelle, 2015) által kidolgozott algoritmusból fejlesztették ki., Revelle (2015a) szerint ez az eljárás a Jackson and Agunwamba (1977) eredeti definíciójához leghűségesebb formát alkalmazza, és további előnye, hogy vektort vezet be a tételek fontosságának súlyozására (Al-Homidan, 2008).
elméleti erősségei ellenére a GLB-t nagyon kevéssé használták, bár néhány közelmúltbeli empirikus tanulmány kimutatta,hogy ez az együttható jobb eredményeket eredményez, mint az α (Lila et al., 2014) és α És ω (Wilcox et al., 2014)., Mindazonáltal kis mintákban, a normalitás feltételezése mellett, hajlamos túlbecsülni a valódi megbízhatósági értéket (Shapiro and ten Berge, 2000); azonban nem normális körülmények között történő működése ismeretlen, különösen akkor, ha az elemek eloszlása aszimmetrikus.
figyelembe véve a fent meghatározott együtthatókat, valamint mindegyik torzítását és korlátozását, e munka célja ezen együtthatók szilárdságának értékelése aszimmetrikus elemek jelenlétében, figyelembe véve a tau-egyenértékűség feltételezését és a minta méretét is.,
Módszerek
Adatok Generációs
Az adatok felhasználásával R (R Development Core Team, 2013), valamint RStudio (Racine, 2012) szoftver, a következő a faktoriális modell:
ahol Xij a szimulált válasz hatálya alá azt a tételt, j, λjk a terhelés elem j a ” k ” Tényezővel (ami által generált unifactorial modell); Fk a látens faktor által generált egy standardizált normális eloszlás (értem 0 várható értékű, egy szórású 1) ej, az a véletlen mérési hiba minden elem is következő egy standardizált normális eloszlás.,
Ferde elemek: Standard normális Xij volt átalakult, hogy létrehoz a nem normális eloszlások segítségével az eljárás által javasolt Headrick (2002) alkalmazása ötödik rend polinom kódolása:
Szimulált Körülmények
teljesítményének értékelése a megbízhatóság együtthatók (α, ω, GLB, valamint GLBa) dolgoztunk három méretben kapható (250, 500, 1000), két vizsgálati méretek: rövid (6 elem) hosszú (12 tétel), két feltételnek a tau-egyenértékűség (az egyik tau-egyenértékűségi egyik nélkül, azaz,, congeneric) és az aszimmetrikus elemek fokozatos beépítése (az összes elem normálistól kezdve az összes elem aszimmetrikusáig). A rövid teszt a megbízhatóság volt beállítva 0.731, amely jelenlétében tau-egyenértékűségi érhető el a hat elemek tényező kirakodás = 0.558; míg a congeneric modell által megszerzett beállítás tényező a kirakodás értékeit 0.3, 0.4, 0.5, 0.6, 0.7, pedig 0,8 (lásd i. Függelék). A 12 tétel hosszú tesztje során a megbízhatóságot 0-ra állították.,845 ugyanazokat az értékeket veszi figyelembe, mint a rövid tesztben mind a tau-egyenértékűség, mind a kongener modell esetében (ebben az esetben a lambda minden értékére két tétel volt). Ily módon 120 körülményt szimuláltak 1000 replikával minden esetben.
Adatelemzés
a fő elemzéseket a Psych (Revelle, 2015b) és a GPArotation (Bernaards and Jennrich, 2015) csomagok segítségével végezték, amelyek lehetővé teszik az α És ω becslését. Két számítógépes megközelítést alkalmaztak a GLB: glb becslésére.fa (Revelle, 2015a) és glb.,algebrai (Moltner and Revelle, 2015), utóbbi olyan szerzők munkái, mint Hunt and Bentler (2015).
annak érdekében, hogy értékeljük a különböző becslések pontosságát a megbízhatóság helyreállításában, kiszámítottuk a hiba gyökere átlagos négyzetét (RMSE), valamint az elfogultságot. Az első a becsült és a szimulált megbízhatóság közötti különbségek átlaga, és a következőképpen formálódik:
ahol ρ^ az egyes együtthatók becsült megbízhatósága, ρ a szimulált megbízhatóság és Nr a replikák száma., A % elfogultság az értendő, hogy a különbséget az jelenti, hogy a becsült megbízhatóságát, valamint a szimulált megbízhatóság, definíciója:
mindkét index, annál nagyobb az érték, annál nagyobb a pontatlanság, a becslő, de ellentétben RMSE, az előítélet lehet pozitív vagy negatív; ebben az esetben további információra lenne szerzett arról, hogy az együttható alábecsüli, vagy túlbecsüli a szimulált megbízhatóság paraméter., Az RMSE < 0,05 és % bias < 5% értékeit a Hoogland and Boomsma (1998) ajánlása alapján elfogadhatónak tekintették.
eredmények
a fő eredmények az 1.táblázatban (6 tétel) és a 2. táblázatban (12 tétel) láthatók. Ezek azt mutatják, hogy az együtthatók RMSE és % -OS torzulása tau-egyenértékűségben és kongener körülmények között van, és hogy a vizsgálati Eloszlás torzulása hogyan növekszik az aszimmetrikus elemek fokozatos beépítésével.
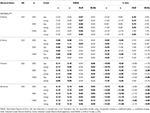
1.táblázat., RMSE és torzítás tau-egyenértékűséggel és kongener feltétel 6 tételre, három mintaméretre és a ferde tételek számára.
2. táblázat. RMSE és torzítás tau-egyenértékűséggel és kongener feltétellel 12 tételre, három mintaméretre és a ferde tételek számára.
csak tau-egyenértékűség és normalitás feltételei mellett (ferdeség < 0.2) megfigyelhető, hogy az α-együttható helyesen becsüli meg a szimulált megbízhatóságot, mint például ω., A kongenerikus állapotban ω korrigálja az α alulbecslését. Mind a GLB, mind a GLBa pozitív torzítást mutat a normalitás alatt, azonban a GLBa megközelítőleg ½ % – kal kevesebb torzítást mutat, mint a GLB (lásd 1.táblázat). Ha figyelembe vesszük a minta méretét, megfigyeljük, hogy a teszt méretének növekedésével a GLB és a GLBa pozitív torzulása csökken,de soha nem tűnik el.
aszimmetrikus körülmények között az 1.táblázatban azt látjuk, hogy mind az α, mind az ω elfogadhatatlan teljesítményt mutat az RMSE növekedésével és alulbecslésekkel, amelyek elérhetik a torzítást> 13% az α együttható esetében (ω esetén 1-2% – kal alacsonyabb)., A GLB és a GLBa együtthatók alacsonyabb RMSE-t mutatnak, ha a vizsgálati torzítás vagy az aszimmetrikus elemek száma nő (lásd az 1., 2. táblázatot). A GLB-együttható jobb becsléseket mutat, ha a teszt nyárs értéke 0,30 körül van; a GLBa nagyon hasonló, jobb becsléseket mutat, mint az ω, a vizsgálati nyárs értéke 0,20 vagy 0,30 körül van. Ha azonban a nyárs értéke 0,50-re vagy 0,60-ra emelkedik, a GLB jobb teljesítményt nyújt, mint a GLBa. A vizsgálati méret (6 vagy 12 ítélem) sokkal fontosabb hatással van, mint a minta mérete a becslések pontosságára.,
a Vita
ebben A vizsgálatban négy tényező manipulálták: tau-egyenértékűségi vagy congeneric modell, minta mérete (250, 500, 1000), a szám a vizsgált tételek (6, 12), valamint a számos aszimmetrikus elemek (0 aszimmetrikus elemek az összes elem, hogy aszimmetrikus) annak érdekében, hogy értékelje a lelkesedés, hogy a jelenléte aszimmetrikus adatok a négy megbízhatóság együtthatók elemzése. Ezeket az eredményeket az alábbiakban tárgyaljuk.,
tau-egyenértékűség esetén az α És ω együtthatók konvergálnak, azonban tau-egyenértékűség (kongener) hiányában az ω mindig jobb becsléseket és kisebb RMSE és % – OS torzítást mutat, mint az α. Ebben a reálisabb állapotban tehát (zöld és Yang, 2009a; Yang és zöld, 2011) az α negatív elfogult megbízhatósági becslővé válik (Graham, 2006; Sijtsma, 2009; Cho és Kim, 2015), az ω pedig mindig előnyösebb, mint α (Dunn et al., 2014). A normalitás feltételezésének megsértése esetén az ω az összes értékelt együttható legjobb becslése (Revelle and Zinbarg, 2009).,
a minta méretéhez fordulva megfigyeljük, hogy ennek a tényezőnek a normalitás alatt kis hatása van, vagy kissé eltér a normalitástól: az RMSE és az elfogultság csökken, amikor a minta mérete növekszik. Mindazonáltal elmondható, hogy e két együttható esetében, a minta mérete 250 és normalitás, viszonylag pontos becsléseket kapunk (Tang and Cui, 2012; Javali et al., 2011)., A GLB és a GLBa együtthatók esetében, mivel a mintaméret növeli az RMSE-t, és az elfogultság általában csökken; ugyanakkor pozitív előítéletet tartanak fenn a normalitás állapotára vonatkozóan még az 1000 nagy mintaméreteknél is (Shapiro és ten Berge, 2000; ten Berge és Sočan, 2004; Sijtsma, 2009).
a tesztméretnél általában nagyobb RMSE-t és torzítást figyelünk meg 6 tételnél, mint a 12-nél, ami arra utal, hogy minél nagyobb az elemek száma, annál alacsonyabb az RMSE és a becslők elfogultsága (Cortina, 1993). Általában a tendencia mind a 6, mind a 12 tétel esetében fennmarad.,
amikor megvizsgáljuk az aszimmetrikus elemek fokozatos beépítésének hatását az adatkészletbe, megfigyeljük, hogy az α-együttható nagyon érzékeny az aszimmetrikus elemekre; ezek az eredmények hasonlóak a Sheng and Sheng (2012), valamint a Green and Yang (2009b) által talált eredményekhez. Az ω koefficiens hasonló RMSE és torzítási értékeket mutat az α értékéhez, de valamivel jobb, még tau-egyenértékűséggel is. A GLB és a GLBa jobb becsléseket mutat, ha a vizsgálat torzulása eltér a 0-hoz közeli értékektől.
figyelembe véve, hogy a gyakorlatban gyakori az aszimmetrikus adatok megtalálása (Miceri, 1989; Norton et al.,, 2013; Ho and Yu, 2014), Sijtsma javaslata (2009) a GLB, mint a megbízhatóság becslése tűnik megalapozott. Más szerzők, mint például a Revelle and Zinbarg (2009) és a Green and Yang (2009a), ω használatát javasolják, azonban ez az együttható csak jó eredményeket hozott a normalitás állapotában, vagy alacsony arányban a nyárs elemek. Mindenesetre ezek az együtthatók nagyobb elméleti és empirikus előnyöket mutattak, mint az α. Ennek ellenére azt javasoljuk a kutatóknak, hogy ne csak a pontos becsléseket tanulmányozzák, hanem az intervallumbecslést is használják (Dunn et al., 2014).,
ezek az eredmények a szimulált körülményekre korlátozódnak, és feltételezhető, hogy nincs összefüggés a hibák között. Ez szükségessé tenné további kutatások elvégzését a különböző megbízhatósági együtthatók összetettebb többdimenziós struktúrákkal való működésének értékeléséhez (Reise, 2012; Green and Yang, 2015), valamint olyan ordinális és/vagy kategorikus adatok jelenlétében, amelyekben a normalitás feltételezésének be nem tartása a norma.
következtetés
amikor a teljes vizsgálati pontszámok általában eloszlanak (azaz,, az összes elem általában eloszlik) ω legyen az első választás, amelyet α követ, mivel elkerülik a GLB által bemutatott túlbecsülési problémákat. Azonban, ha van egy alacsony vagy mérsékelt teszt nyárs GLBa kell használni. A GLB akkor ajánlott, ha az aszimmetrikus elemek aránya magas, mivel ilyen körülmények között mind az α, mind az ω megbízhatósági becslőként történő használata nem ajánlott, függetlenül a minta méretétől.
szerzői hozzájárulások
a kutatási és elméleti keret (IT, JA) fogalmának kidolgozása. A módszertani keret felépítése (IT, JA)., Az R nyelvi szintaxis (IT, JA) fejlesztése. Az adatok elemzése és értelmezése (IT, JA). Az eredmények megvitatása a jelenlegi elméleti háttér fényében (JA, IT). A cikk elkészítése és írása (JA, IT). Általában mindkét szerző egyformán hozzájárult e munka fejlődéséhez.,
finanszírozás
az első szerző nyilvánosságra megkapta a következő pénzügyi támogatást a kutatás, szerzőség, és / vagy közzététele ezt a cikket: pénzügyi támogatást kapott a chilei Nemzeti Bizottság tudományos és technológiai kutatás (CONICYT) “Becas Chile” doktori Ösztöndíj program (támogatási szám: 72140548).
összeférhetetlenségi nyilatkozat
a szerzők kijelentik, hogy a kutatást olyan kereskedelmi vagy pénzügyi kapcsolatok hiányában végezték, amelyek potenciális összeférhetetlenségnek tekinthetők.
Cronbach, L. (1951)., Az alfa-együttható és a vizsgálatok belső szerkezete. Psychometrika 16, 297-334. doi: 10.1007/BF02310555
CrossRef teljes szöveg/Google Scholar
McDonald, R. (1999). Tesztelmélet: egységes kezelés. Mahwah, NJ: Lawrence Erlbaum Associates.
Google Scholar
R Development Core Team (2013). R: a statisztikai Számítástechnika nyelve és környezete. Bécs: R Alapítvány statisztikai Számítástechnika.
Raykov, T. (1997)., Scale reliability, cronbach”s coefficient alpha, and violations of essential tau- equivalence with fixed congeneric components. Multivariate Behav. Res. 32, 329–353. doi: 10.1207/s15327906mbr3204_2
PubMed Abstract | CrossRef Full Text | Google Scholar
Raykov, T. (2001). Bias of coefficient alpha for fixed congeneric measures with correlated errors. Appl. Psychol. Meas. 25, 69–76. doi: 10.1177/01466216010251005
CrossRef Full Text | Google Scholar
Revelle, W. (2015b). Package “psych.,”Elérhető online: http://org/r/psych-manual.pdf
Shapiro, A., and ten Berge, J. M. F. (2000). A minimális nyomtényező-analízis aszimptotikus torzulása, a megbízhatósághoz leginkább kötődő alkalmazásokkal. Psychometrika 65., 413-425. doi: 10.1007/BF02296154
CrossRef teljes szöveg/Google Scholar
ten Berge, J. M. F., And Sočan, G. (2004). A legnagyobb alsó határ a teszt megbízhatóságához és az unidimenzionalitás hipotéziséhez kötődik. Psychometrika 69, 613-625. doi: 10.,1007 / Bf02289858
CrossRef Full Text | Google Scholar
Woodhouse, B., and Jackson, P. H. (1977). A nem homogén elemekből álló teszt teljes pontszámának megbízhatóságának alsó határai: II: keresési eljárás a legnagyobb alsó határ megtalálására. Psychometrika 42, 579-591. doi: 10.1007/BF02295980
CrossRef teljes szöveg/Google Scholar
I. függelék
r szintaxis a Pearson korrelációs mátrixainak megbízhatósági együtthatóinak becsléséhez., Az átlón kívüli korrelációs értékeket úgy számítjuk ki, hogy megszorozzuk az elemek faktorterhelését: (1) tau-ekvivalens modell mindegyik egyenlő 0,3114-gyel (λiλj = 0,558 × 0,558 = 0,3114) és (2) kongenerikus modell ezek a különböző faktorterhelés függvényében változnak (például az A1, 2 = λ1λ2 = 0,3 × 0,4 = 0,12 mátrixelem). Mindkét példában az igazi megbízhatóság 0,731.
> omega(Cr,1)$alpha # standardized Cronbach”s α
0.731
> omega(CR,1)$omega.tot # együttható ω összesen
0.,731
> glb.fa(Cr)$glb # GLB factorial procedure
0.731
> glb.algebraic(Cr)$glb # GLB algebraic procedure
0.731
> omega(Cr,1)$alpha # standardized Cronbach”s α
0.717
> omega(Cr,1)$omega.tot # coefficient ω total
0.731
> glb.fa(Cr)$glb # GLB factorial procedure
0.754
> glb.algebraic(Cr)$glb # GLB algebraic procedure
0.731