Pythagoras “tétel

Pythagoras

Több mint 2000 évvel ezelőtt csodálatos felfedezés volt a háromszögekről:

amikor egy háromszögnek derékszöge van (90°) …

… a négyzetek mindegyikén készülnekhárom oldalról …

… ezután a legnagyobb négyzet pontosan ugyanaz a terület,mint a másik két négyzet együtt!,

Ez az úgynevezett “Pitagorasz” Tétel” meg lehet írni egy rövid egyenlet:

a2 + b2 = c2

Megjegyzés:

• c a leghosszabb oldalán a háromszög
• a b a másik két oldala

Definíció

A leghosszabb oldala a háromszögnek az úgynevezett “átfogó”, tehát a hivatalos meghatározás:

biztos … ?

nézzük meg, hogy valóban működik-e egy példa segítségével.

miért hasznos ez?

ha ismerjük a derékszögű háromszög két oldalának hosszát, akkor megtaláljuk a harmadik oldal hosszát. (De ne feledje, hogy csak a derékszögű háromszögeken működik!)

hogyan kell használni?,

Írd le, mint egy egyenlet:

Akkor használja, hogy megtalálja a hiányzó érték, mint ezek a példák:

Azt is olvastam, Négyzet, Négyzet, Gyökerek, hogy megtudja, miért √169 = 13

működik fordítva is: ha a három oldalán egy háromszög, hogy a2 + b2 = c2, akkor a háromszög megfelelő szögben.,

és Ön is bizonyíthatja a tételt !

szerezzen papírtollat és ollót, majd a következő animációt használja útmutatóként:

• rajzoljon egy derékszögű háromszöget a papírra, sok helyet hagyva.,
• Felhívni a tér mentén az átfogó (a leghosszabb oldal)
• Draw-az azonos méretű, négyzet, a másik oldalon az átfogó
• vonalakat, mint ahogy azt az animáció, mint ez:
• 
• Vágd ki a formákat
• Rendezni őket, így lehet bizonyítani, hogy a nagy tér van ugyanazon a területen, mint a két négyzet a másik oldalon

a Másik, Elképesztően Egyszerű, Bizonyíték

Itt az egyik legrégebbi bizonyíték arra, hogy a tér a hosszú oldalon ugyanazon a területen, mint a többi négyzet.,

nézze meg az animációt, és figyeljen, amikor a háromszögek elkezdenek csúszni.

érdemes néhányszor megnézni az animációt, hogy megértsük, mi történik.

a lila háromszög a fontos.

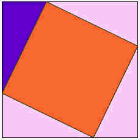lesz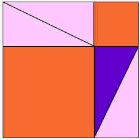