“i, bármely értékeld, meg vagyok győződve arról, hogy nem dob kockát.,”
~ Albert Einstein
- Véletlen Változók
- Diszkrét Véletlen Változók
- Folytonos Véletlen Változók
- Vegyes Véletlen Változók
- Kumulatív Eloszlás Függvények (CDF)
- sűrűségfüggvényt (PDF)
- Interaktív CDF/PDF Példa
a Véletlen Változók:

mondtam, hogy egy érme a zsebéből, majd dobd be a levegő. Miközben az űrben repül, mit mondhat a jövőjéről?
le fog szállni? Írás?, Sőt, mennyi ideig marad a levegőben? Hányszor fog ugrálni? Milyen messze van attól, ahol először eléri a talajt, végül pihenni fog? Ami azt illeti, valaha is a földre kerül? Valaha pihenni?
néhány ilyen kérdés esetén már jóval a megfigyelések előtt meg tudunk és meg is tudunk állapodni a válaszokkal; biztosak vagyunk benne, hogy a gravitáció megmarad, és az érme le fog szállni. De másoknak nincs más választásunk, mint ítélkezni és homályosabban beszélni, ha a jövőről bármi hasznosat akarunk mondani.,
mint tudósok, természetesen a mi feladatunk valami hasznosat mondani(vagy legalábbis hiteles…), míg a fontos fizikai rendszer metaforikus érméi még mindig a levegőben vannak. A fej vagy a farok akár élet vagy halál kérdése is lehet. Érméink lehetnek például különböző hűtőfolyadék-áramlási sebesség vagy urán tömeg egy atomerőműben. Nagyon érdekel, hogy mi az esélye, hogy mi lesz örvénylő turbinák helyett olvadás.,
szigorú deterministának az összes ilyen fogadást jóval azelőtt rendezték, hogy bármilyen érmét, metaforikus vagy sem, valaha verték volna; egyszerűen még nem tudjuk. Ha csak tudtuk, hogy az erők alkalmazott egy érme dobás, pontos eloszlása tömeg, a különböző perc mozgását levegő a szobában… Ha mindezt tudnánk, akkor tudnánk, hogy az adott pénzfeldobásnak 100% esélye van arra, hogy úgy landoljon, ahogy leszáll, és nulla esélye van bármilyen más eredményre.
de természetesen gyakran hiányzik még a világ ilyen ismereteinek említhető töredéke is., Ráadásul rendkívül kicsi skálán úgy tűnik, hogy a szigorú deterministák teljesen tévednek; nem lehet megjósolni, hogy például egy urán atom mikor oszlik meg, és ha egy ilyen esemény befolyásolja a nagyobb világot, akkor ez a makró esemény valóban kiszámíthatatlan. Egyes eredmények valóban fel a levegőben, nyugtalan, amíg azok a múlt része.
annak érdekében, hogy megbirkózzunk ezzel a valósággal, és hogy egy rendszer jövőbeli állapotait valamilyen hasznos módon le tudjuk írni, véletlenszerű változókat használunk., A véletlenszerű változó egyszerűen egy olyan funkció, amely a rendszer minden lehetséges fizikai kimenetelét egy egyedi, valós számhoz kapcsolja. Mint ilyen, háromféle véletlenszerű változó létezik: diszkrét, folyamatos és vegyes. A következő szakaszokban ezeket a kategóriákat röviden ismertetjük, majd példákat adunk.
diszkrét véletlen változók:
fontolja meg újra a pénzfeldobást. Lehet, hogy fejünk vagy farkunk van, amennyire csak lehetséges. Ha meghatároztunk egy változót, x, mint a fejek száma egyetlen dobásban, akkor x lehet 1 vagy 0, semmi más., Egy ilyen függvény, x, példa lenne egy diszkrét véletlenszerű változóra. Az ilyen véletlenszerű változók csak diszkrét értékeket vehetnek fel. Más példák a terhességi teszt lehetséges eredményei, vagy az osztályteremben lévő hallgatók száma.
folyamatos véletlen változók:
vissza a pénzfeldobáshoz, mi lenne, ha leírnánk azt a távolságot, ahol az érménk pihent, és ahol először a földre esett. Ez a távolság, x, folyamatos véletlenszerű változó lenne, mert végtelen számú értéket vehet fel a valós számok folyamatos tartományán belül., Az érme 1 cm-t, 1,1 cm-t, vagy 1,11 cm-t, vagy tovább haladhat. A folyamatos véletlenszerű változók további példái a galaxisunkban lévő csillagok tömege, az óceán vizeinek pH-ja vagy néhány analit tartózkodási ideje egy gázkromatográfban.
vegyes véletlen változók:
vegyes véletlen változók mind diszkrét, mind folyamatos komponensekkel rendelkeznek. Az ilyen véletlenszerű változók ritkán fordulnak elő. Egy lehetséges példa, bár, lehet, hogy méri a minta súlyát, és úgy dönt, hogy minden súly mért negatív értéket kap egy értéke 0., Így a véletlen változónak diszkrét komponense van x = 0-nál, és folytonos komponense, ahol x > 0.
kumulatív eloszlási függvények (CDF):
természetesen felmerül a kérdés, hogy hogyan lehet a legjobban matematikailag leírni (és vizuálisan megjeleníteni) a véletlenszerű változókat. Ezekhez a feladatokhoz valószínűségi sűrűségfüggvényeket (PDF) és kumulatív sűrűségfüggvényeket (CDF) használunk. Mivel a CDFs egyszerűbb megérteni mind a diszkrét, mind a folyamatos véletlenszerű változókat, mint a PDF-eket, először elmagyarázzuk a CDFs-t.
fontolja meg a tisztességes 6 oldalú kocka dobását., Mi lenne a 1 ban ben 6 esélye, hogy bármely lehetséges értékét a véletlen változó (1, 2, 3, 4, 5, vagy 6). Ha ezeket a lehetséges értékeket az x tengelyen ábrázoljuk, és az y tengelyen ábrázoljuk az egyes értékek, x vagy az X-nél kisebb értékek mérésének valószínűségét, akkor a véletlenszerű változó CDF-je lesz.
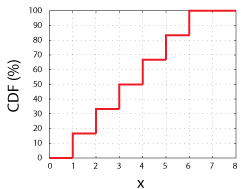
CDF egy tisztességes 6 oldalirányú kocka számára. Vegye figyelembe, hogy minden lépés magassága 16,67%, vagy 1 A 6-ban.
Ez a funkció, a CDF (x) egyszerűen elmondja nekünk az X-ig terjedő értékek mérésének esélyeit., Mint ilyen, minden CDFs mind ezek a jellemzők:
- A CDF kell egyenlő 0, ha x = -∞, valamint megközelítés 1 (vagy 100%) x megközelítések +∞. Egyszerűen fogalmazva, az összes lehetséges kimenetel közül eredménynek kell lennie; a hatoldalas kocka dobásának esélye, valamint a -∞ és ∞ közötti érték elérése 100%.
- a CDF lejtésének mindig nullával vagy annál nagyobbnak kell lennie. Vegyük például annak az esélyét, hogy egy 6 oldalas kockát dobjunk (tisztességes vagy sem), és 0 és 4 közötti értéket kapjunk., Ez az esély valószínűleg nem lehet több, mint a 0 és 5 közötti érték megszerzésének esélye, mivel az 1, 2 vagy 3 leszállás esélye felfelé természetesen mindig az 1, 2, 3 vagy 4 esélyeinek egy töredéke lesz.
egy folyamatos véletlenszerű változó példáján a következő kisalkalmazás mutatja a normálisan elosztott CDF-et.,div>
| -5 | 5 |
| x | |
This important distribution is discussed elsewhere., Egyszerűen vegye figyelembe, hogy a jellemzői A CDF fent leírt magyarázata egy diszkrét véletlen változó hold folyamatos véletlen változók is.
a CDFs tulajdonságainak intuitívabb példáit lásd az alábbi interaktív példában. Továbbá, interaktív telkek sok más CDFs fontos a statisztika területén használt ezen az oldalon megtalálható itt.
valószínűségi Sűrűségfüggvények (PDF):
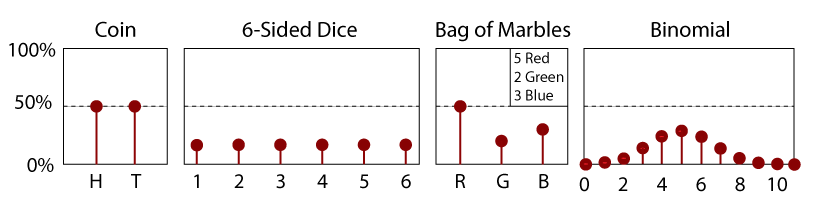
PDF egy tisztességes 6 oldalú kockához.
A PDF egyszerűen egy CDF származéka., Így a PDF egy véletlenszerű változó, x függvénye is, amelynek nagysága jelzi egy adott érték mérésének relatív valószínűségét. Mivel ez egy CDF lejtése, a PDF-nek mindig pozitívnak kell lennie; semmilyen eseményre nincs negatív esély. Ezenkívül definíció szerint A -∞ és x közötti PDF(x) görbe alatti terület megegyezik a CDF(x) értékével. Mint ilyen, a két x1 és x2 érték közötti terület megadja annak a valószínűségét,hogy egy értéket ezen a tartományon belül mérnek.
a következő kisalkalmazás egy példát mutat a PDF-re egy normálisan elosztott véletlenszerű változóhoz, x-hez.,
Normal PDF
|
x:
| mean:
| stdev:
| f(x):
|
|
Notice, when the mean and standard deviations are equal, how the PDF correlates with the normal CDF in the section above., a folytonos és diszkrét PDF közötti különbséget is figyelembe kell venni. Míg egy diszkrét PDF (mint például a fenti kocka) megadja az esélye, hogy egy adott eredmény, valószínűségek folyamatos PDF számít tartomány, nem diszkrét pontokat. Például egyértelműen van egy 1 A 6-ban (16.6%) esélye egy 3 dobásra, amint az a PDF-ben látható. De mi a furcsa, ha pontosan nullát mérünk egy véletlenszerű változóval, amelynek normál PDF-értéke nulla, amint az fent látható? Annak ellenére, hogy ez az érték, ahol a PDF a legnagyobb, az esélye a mérési pontosan 0.00000..,. talán intuitív módon ellentétes, nulla. Az esélye, hogy egy adott véletlen számot végtelen pontossággal mérjünk, valójában nulla. folyamatos PDF-fájl esetén ehelyett megkérdezheti, hogy mi az esélye annak, hogy két érték között mérje meg a nullánál nagyobb valószínűséget. Ennek a valószínűségnek a megtalálásához egyszerűen a véletlenszerű változónk CDF-jét használjuk., Mivel a CDF azt mondja nekünk, hogy páratlan az érték mérése, vagy bármi alacsonyabb, mint ez az érték, hogy megtaláljuk a két érték, x1 és x2 közötti mérés valószínűségét (ahol x1 > x2), egyszerűen meg kell vennünk a CDF értékét x1-en, és kivonjuk belőle a CDF értékét x2-EN. Például, ha a normál CDF-et használjuk a fenti kisalkalmazásban (μ=0, σ=1), Ha meg akarjuk tudni a 0.01 és 0.02 közötti mérési esélyeket, akkor CDF(x=0.1)=53.9828% és CDF(x=0.2)=57.9260%. Ezután a különbség, CDF(0.2)-CDF(0.1), ad nekünk az esélye körülbelül 3.9% mérési x között 0.1 és 0.2., a PDF-ek tulajdonságainak intuitív, vizuális példáit lásd az alábbi interaktív példában. Ezen az oldalon számos fontos PDF-fájl interaktív parcellái is láthatók. |
|||||||||||||||||