Tartalom
Valószínűség-sűrűség funkciók
A sűrűségfüggvényt (pdf) \(f(x)\) egy folytonos eloszlású véletlen változó \(X\) meghatározott, a származékos, a cdf \(F(x)\):
\
Ez néha hasznos, hogy fontolja meg a cdf \(F(x)\) a szempontból, hogy a pdf \(f(x)\):
\
A pdf \(f(x)\) két fontos tulajdonságok:
- \(f(x) \geq 0\), mind a \(x\)
- \(\displaystyle\int_{-\infty}^{\infty} f(x)\;dx = 1\).,
végtelen sokféle alakzat lehetséges egy pdf számára, mivel az egyetlen követelmény a fenti két tulajdonság. A pdf-nek lehet egy vagy több csúcsa, vagy egyáltalán nincs csúcs; lehetnek megszakítások, funkciók kombinációiból állhatnak stb. az 5. ábra egy egyetlen csúcsú pdf-et mutat, némi enyhe nyárssal. Mint egy tipikus pdf esetében, a függvény értéke nulla, mint \(x \to \infty\) és \(x \to -\infty\).
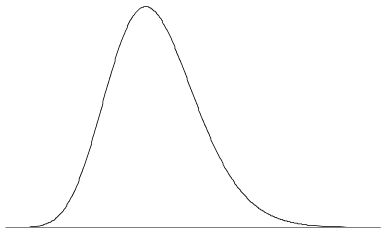
5.ábra: a pdf így nézhet ki.,
most azt vizsgáljuk, hogy a \(X\) folyamatos véletlenszerű változóval kapcsolatos valószínűségek hogyan kapcsolódnak a pdf-hez. A fontos eredmény itt az, hogy
\ _a^b.\]
Ez az eredmény abból a tényből következik, hogy mindkét oldal egyenlő \(F(B) – F(a)\).
Megjegyzések.
- egy folyamatos véletlenszerű változó esetében figyelembe kell vennünk annak valószínűségét, hogy egy intervallumban fekszik. Ennek az eredménynek az a jelentősége, hogy azt mondja nekünk, hogy a valószínűség megtalálásához meg kell találnunk A PDF alatti területet az adott intervallumban.
- a pdf teljes területe 1., Tehát ez az eredmény azt mondja nekünk, hogy ahhoz, hogy megközelítsük azt a valószínűséget, hogy a véletlenszerű változó egy adott intervallumban fekszik, csak meg kell kitalálnunk a PDF alatti terület töredékét az intervallum végei között.
- ez az eredmény egy másik perspektívát ad arra vonatkozóan, hogy a PDF-ek miért nem lehetnek negatívak, mivel ha igen, negatív valószínűség érhető el, ami lehetetlen.
- a pdf analóg, de különbözik a valószínűségi függvénytől (PF) egy diszkrét véletlen változóhoz. A pf valószínűséget ad, így nem lehet nagyobb, mint egy., A pdf \(F(x)\) azonban nagyobb értéket adhat a \(x\) egyes értékeihez, mivel nem a \(f(x)\) értéke, hanem a görbe alatti terület jelenti a valószínűséget. Másrészt a görbe magassága tükrözi a relatív valószínűséget. Ha \(f(B) = 2F(a)\), akkor a \(b\) közelében lévő megfigyelés körülbelül kétszer olyan valószínű, mint egy megfigyelés \(a\) közelében.,
Következő oldal – Tartalom – Jelent s eltérést, egy folytonos eloszlású véletlen változó
 |
Ez a kiadvány által finanszírozott Ausztrál Kormány Oktatási Minisztérium, a Foglalkoztatás, illetve a Munkahelyi Kapcsolatok |
Közreműködők Kifejezés használata |