8.1 a történelmi példa
könyvében a két új tudomány, Galileo Galilea (1564-1642) számos érvet ad annak bizonyítására, hogy nem lehet olyan dolog, mint a tényleges végtelenség vagy a tényleges végtelenség. Az egyik érvét a következő módon lehet rekonstruálni. A Galileo azt javasolja, hogy feltételezzük, hogy a természetes számok tényleges végtelenek (a természetes számok a pozitív egész számok 1-től):
{1, 2, 3, 4, 5, 6, 7, ….,}
azt is javasolja, hogy feltételezzük, hogy a természetes számok négyzeteinek tényleges végtelensége van.
{1, 4, 9, 16, 25, 36, 49, ….}
most, Galileo okokból, vegye figyelembe, hogy ez a két csoport (ma “készleteknek” neveznénk őket) azonos méretű. Ezt láthatjuk, mert láthatjuk, hogy a két csoport között egy-egy levelezés van.,
| {1, | 2, | 3, | 4, | 5, | 6, | 7, ….,div> | |
| {1, | 4, | 9, | 16, | 25, | 36-os | 49, …} |
Ha meg tudjuk társítani minden természetes szám egyetlen egy tér szám, ha tudjuk társítani minden téren szám egyetlen egy természetes szám, akkor ezek a készletek kell az azonos méretű.,
de várjon egy pillanatot, mondja Galileo. Nyilvánvalóan sokkal több természetes szám van, mint négyzetszámok. Vagyis minden négyzetszám szerepel a természetes számok listáján, de sok természetes szám nem szerepel a négyzetszámok listáján. A következő számok mind a természetes számok listáján szerepelnek, de nem a négyzetszámok listáján.
{2, 3, 5, 6, 7, 8, 10, ….,}
tehát, Galileo okokból, ha a természetes számok csoportjában sok olyan szám van, amely nem szerepel a négyzetszámok csoportjában, és ha a négyzetszámok csoportjában nincsenek olyan számok, amelyek nem szerepelnek a naturals számokban, akkor a természetes számok nagyobbak, mint a négyzetszámok. És ha a természetes számok csoportja nagyobb, mint a négyzetszámok csoportja, akkor a természetes számok és a négyzetszámok nem azonos méretűek.,
két következtetést vontunk le: a természetes számok halmaza és a négyzetszámok halmaza azonos méretű; a természetes számok halmaza és a négyzetszámok halmaza nem azonos méretű. Ez ellentmondásos.
Galileo azt állítja, hogy az ellentmondás oka az, hogy feltételeztük, hogy vannak tényleges végtelenségek. Ezért arra a következtetésre jut, hogy nincsenek tényleges végtelenségek.
8.2 közvetett bizonyítékok
logikánk még nem elég erős ahhoz, hogy néhány érvényes érvet bizonyítsunk. Vegyük példaként a következő érvet.,
(P→(QvR))
Q
r
p
Ez az érv érvényesnek tűnik. Az első feltevést tudjuk: ha P igaz, akkor így lenne (Q v R) igaz legyen. De akkor vagy Q vagy R vagy mindkettő igaz lenne. A második és harmadik helyen pedig tudjuk: a K hamis, az R pedig hamis. Tehát nem lehet, hogy (Q v R) igaz, tehát nem lehet, hogy P igaz.
az érvet egy igazságtáblázat segítségével ellenőrizhetjük. Asztalunk összetett lesz, mert az egyik előfeltételünk összetett.,
In any kind of situation in which all the premises are true, the conclusion is true., Vagyis: a helyiségek csak az utolsó sorban igazak. Ebben a sorban a következtetés is igaz. Tehát ez egy érvényes érv.
de szánjon egy percet, és próbálja bizonyítani ezt az érvet. Kezdjük

és most megállunk. Egyik szabályunkat sem alkalmazhatjuk. Itt van egy érvényes érv, hogy még nem tette a érvelési rendszer elég erős ahhoz, hogy bizonyítani.
számos módja van, hogy orvosolja ezt a problémát, és hogy a mi érvelési rendszer elég erős., Az egyik legrégebbi megoldás egy új bizonyítási módszer bevezetése, amelyet hagyományosan “reductio ad absurdum” – nak neveznek, ami az abszurditás csökkentését jelenti. Ezt a módszert gyakran “közvetett bizonyítéknak” vagy “közvetett származtatásnak”is nevezik.
az ötlet az, hogy feltételezzük a következtetésünk megtagadását, majd megmutatjuk, hogy az ellentmondás eredménye. Az ellentmondás akkor jelenik meg, amikor valamilyen mondatot bizonyítunk Ψ, és annak tagadása Ψ. Ez bármilyen mondat lehet. A lényeg az, hogy a kétértelműség elvét figyelembe véve valami hamisnak kellett bizonyítanunk. Mert ha Ψ igaz, akkor Ψ hamis; és ha Ψ igaz, akkor Ψ hamis., Nem kell tudnunk, hogy melyik hamis (Ψ vagy Ψ); elég tudni, hogy az egyiknek kell lennie.
ne feledje, hogy logikai rendszerünket úgy építettük fel, hogy valódi kijelentésekből ne lehessen hamisságot előállítani. A közvetett levezetésben előidézett hamisság forrásának tehát valamilyen hamisságnak kell lennie, amelyet hozzáadtunk érvünkhöz. És amit hozzátettünk az érveléshez, az a következtetés megtagadása. Így a következtetésnek igaznak kell lennie.,
Az argumentum alakja a következő:

hagyományosan a közvetett származtatás feltételezését”reduktio feltételezésének” is nevezik.
konkrét példaként bizonyíthatjuk zavaró esetünket.

a 4-es vonalon feltételeztük a következtetésünk megtagadását. A következtetés, amit helyesnek hittünk, P volt, és ennek a tagadása P. a 7. sorban, bebizonyítottuk R., Technikailag ezen a ponton végeztünk, de szeretnénk kedvesek lenni bárkinek, aki megpróbálja megérteni a bizonyítékunkat, ezért megismételjük a 3. sort, hogy az R és R mondatok egymás mellett legyenek, és nagyon könnyű látni, hogy valami rosszul ment. Vagyis ha bebizonyítottuk mind az R, mind az R-t, akkor bebizonyítottuk, hogy valami hamis.
érvelésünk most így megy. Mi történt rosszul? Vonal 8 helyes használata ismétlés; vonal 7 származik a helyes használata modus tollendo ponens; vonal 6 a helyes használata modus ponens; vonal 5 a helyes használata kettős tagadás., Tehát nem hibáztunk az érvelésünkben. Az 1-es, a 2-es és a 3-as vonalakat használtuk, de azok a helyiségek, amelyeket elfogadtunk, helyesek. Ez elhagyja a 4-es vonalat. Ez lehet az ellentmondásom forrása. Hamisnak kell lennie. Ha a 4. sor hamis, akkor a P igaz.
egyesek a közvetett bizonyítékokat kevésbé erősnek tartják, mint a közvetlen bizonyítékokat. Ennek sok, összetett oka van. De, a mi propositional logika, ezen okok egyike sem vonatkozik. Ez azért van, mert bizonyítani lehet, hogy javaslataink logikája következetes., Ez azt jelenti, hogy bizonyítható, hogy javaslatunk logikája nem bizonyíthat hamisságot, hacsak először nem vezet be hamisságot a rendszerbe. (Általában nem lehet bizonyítani, hogy az erősebb és fejlettebb logikai vagy matematikai rendszerek konzisztensek e rendszerek belsejéből; például az aritmetikában nem lehet bizonyítani, hogy az aritmetika következetes.) Tekintettel arra, hogy biztosak lehetünk a javaslattételi logika következetességében, biztosak lehetünk abban, hogy a javaslattételi logikánkban a közvetett bizonyíték az érvelés jó formája., Tudjuk, hogy ha bebizonyítjuk, hogy a hazugság, mi kell egy hazugság a; ha meg vagyunk győződve arról, hogy minden más feltételezések (a helyszínen) a bizonyíték, kivéve a feltételezés, hogy a közvetett levezetése, akkor biztosak lehetünk abban, hogy ez a feltételezés a közvetett levezetése lehet a forrása a hazugság.
itt egy megjegyzés a terminológiáról. Az “ellentmondás” szót a legtöbb logikai vitában kétértelműen használják. Ez olyan helyzetet jelenthet, mint amilyet fent látunk, ahol két mondatot állítunk be, és ezek a mondatok nem lehetnek igazak., Vagy egyetlen mondatot jelenthet, amely nem lehet igaz. Egy ilyen mondat példája (P^P)., Ennek a mondatnak az igazságtáblája:
| p | p |
|---|---|
| f | |
| t |
így ez a fajta mondat soha nem lehet igaz, függetlenül a P jelentése.,
a kétértelműség elkerülése érdekében ebben a szövegben mindig egyetlen mondatot fogunk hívni, amely nem lehet igaz “ellentmondásos mondat”. Így (P^P) ellentmondásos mondat. Azok a helyzetek, amikor két mondatot állítunk be, amelyek nem lehetnek mind igazak, “ellentmondásnak”nevezzük.
8.3 példánk és más példák
a Galileo érvelésének egy változatát most rekonstruálhatjuk. A következő kulcsot fogjuk használni.
P: vannak tényleges végtelenségek (beleértve a természetes számokat és a négyzetszámokat).,
Q: A természetes számok és a négyzetszámok között egy-egy összefüggés van.
R: a természetes számok halmazának mérete és a négyzetszámok halmazának mérete azonos.
S: minden négyzetszám természetes szám.
T: a természetes számok egy része nem négyzet alakú szám.
U: több természetes szám van, mint négyzetszám.,
ez A kulcs az az érv lesz lefordítva:
(P→Q)
(Q→R)
(P→(S^T))
((S^T)→U)
(U→R)
O
De be tudjuk bizonyítani, hogy ez egy érvényes érv segítségével közvetett származtatása:

A vonal 6, feltételeztük, P mert Galileo hitte, hogy P célja annak bizonyítása, hogy P., Ami azt hitte, hogy nincs tényleges infinities, ezért feltételezte, hogy téves azt hinni, hogy nem ez a helyzet, hogy nincs tényleges infinities. Ez a hamisság más hamisságokhoz vezet, felfedve magát.,
azok számára, akik érdeklődnek: Galileo arra a következtetésre jutott, hogy nincsenek tényleges végtelenségek, de vannak lehetséges végtelenségek. Így indokolta, hogy nem az a helyzet, hogy minden természetes szám létezik (bizonyos értelemben “létezik”), de igaz, hogy a természetes számokat örökre meg lehet számolni. Galileo előtt és után számos filozófus tartotta ezt a nézetet; ez hasonlít Arisztotelész nézetéhez,aki fontos logikusként és filozófusként közel kétezer évvel Galileo előtt írt.,
vegye figyelembe, hogy egy ilyen érvelésnél nem a közvetett származtatás feltételezése, hanem az egyik helyiség volt az ellentmondás forrása. Ma a legtöbb matematikus ezt hiszi Galileo érvéről. Georg Cantor (1845-1918), a halmazelmélet feltalálója szerint a végtelen halmazoknak azonos méretű megfelelő részhalmazai lehetnek., Vagyis Cantor tagadta a fenti 4. feltevést: annak ellenére, hogy az összes négyzetszám természetes szám, és nem minden természetes szám négyzetszám, nem az a helyzet, hogy ez a két készlet különböző méretű. Cantor azonban elfogadta a fenti 2. feltevést, ezért úgy vélte, hogy a természetes számok halmazának mérete és a négyzetszámok halmazának mérete megegyezik. Ma, Cantor érvelése alapján, a matematikusok és a logikusok a végtelenséget tanulmányozzák, és nagy mennyiségű tudást fejlesztettek ki a végtelenség természetéről. Ha ez érdekli Önt, lásd a 17.5 pontot.,
Vegyünk egy másik példát a közvetett származtatás szemléltetésére. A tételek nagyon hasznos halmazát ma “De Morgan tételeinek” nevezik, Augustus De Morgan (1806-1871) logikusa után. Ezeket a 9. fejezetig nem tudjuk teljes mértékben kijelenteni, de angolul meg tudjuk adni az egyenértéküket: DeMorgan megfigyelte, hogy (PvQ) és (P^Q) egyenértékűek, valamint hogy (P^Q) és (PvQ) egyenértékűek. Tekintettel erre, a nyelvünk tételének kell lennie ((PvQ)→(P^Q)). Bizonyítsuk be.
az egész képlet feltételes, ezért feltételes származékot használunk., Bizonyításunknak tehát meg kell kezdődnie:
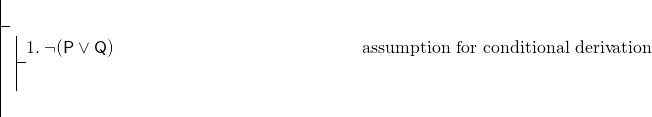
a feltételes származtatás befejezéséhez bizonyítanunk kell (P^Q). Ez egy összefüggés, és a konjunkciók bemutatására vonatkozó szabályunk adjunction. Mivel ennek a szabálynak a használata lehet a legjobb módja a megjelenítésnek (P^Q), törekedhetünk a P megjelenítésére, majd a Q megjelenítésére, majd az adjunktus elvégzésére. De, nyilvánvalóan nagyon kevés a munka-csak vonal 1, ami negáció. Ilyen esetben általában bölcs dolog közvetett bizonyítékot megkísérelni. Kezdje közvetett bizonyíték P.,

most ellentmondást kell találnunk—bármilyen ellentmondást. De már van egy nyilvánvaló. Az 1. sor azt mondja, hogy sem P, sem Q nem igaz. De vonal 3 azt mondja, hogy P igaz. Ezt az ellentmondást egy képlet megtalálásával és annak tagadásával kell kifejezésre juttatnunk. Ezt kiegészítéssel tudjuk megtenni.

a bizonyítás befejezéséhez újra ezt a stratégiát fogjuk használni.

a 9.fejezet problémájaként fogjuk bizonyítani de Morgan tételeit.,
itt van egy általános ökölszabály a bizonyítások elvégzéséhez: feltételes bizonyításkor mindig feltételes származtatást végezzen; ellenkező esetben próbálja meg a közvetlen származtatást; ha ez nem sikerül, akkor próbálja meg az indirekt származtatást.
8.4 problémák
- töltse ki a következő igazolásokat. Mindegyik közvetett származtatást igényel. Az utolsó kettő kihívást jelent.
- Bizonyítsuk be, hogy a következő tételek.
- (P^P).
- (((P→P)^(P→P)).
- (P→(P^Q)).
- ((P^Q)→(P→Q)).
- normál angol nyelven írja be saját érvényes érvét legalább két helyiséggel., Az érvnek csak egy bekezdésnek kell lennie (nem a mondatok rendezett listája vagy bármi más, ami formális logikának tűnik). Fordítsd le propositional logikára, és bizonyítsd, hogy indirekt derivációval érvényes.
a Galileo könyv címének ez a fordítása vált a leggyakoribbá, bár szó szerint inkább matematikai diskurzusok és bemutatók lettek volna. A könyv fordításai közé tartozik Drake (1974).