ANOVA Test: Definizione, Tipologie, Esempi

Condividi su

le Statistiche di Definizioni > ANOVA
Sommario:

ANOVA Test
One Way ANOVA
Due Vie ANOVA
che Cosa è MANOVA?
Che cos’è l’ANOVA fattoriale?
Come eseguire un test ANOVA
ANOVA vs. T
Misure ripetute ANOVA
Sfericità

Il test ANOVA

Che cos’è ANOVA?, Guarda il video per un’introduzione, o continua a leggere qui sotto:

Si prega di accettare statistiche, cookie di marketing per guardare questo video.

Hai ancora problemi? Chegg.com ti abbinerà con un tutor (la tua prima lezione è gratuita!).

Un test ANOVA è un modo per scoprire se i risultati dell’indagine o dell’esperimento sono significativi. In altre parole, ti aiutano a capire se devi rifiutare l’ipotesi nulla o accettare l’ipotesi alternativa.

Fondamentalmente, stai testando i gruppi per vedere se c’è una differenza tra loro., Esempi di quando potresti voler testare diversi gruppi:

Un gruppo di pazienti psichiatrici sta provando tre diverse terapie: consulenza, farmaci e biofeedback. Vuoi vedere se una terapia è migliore delle altre.
Un produttore ha due diversi processi per realizzare lampadine. Vogliono sapere se un processo è migliore dell’altro.
Studenti provenienti da diversi college sostenere lo stesso esame. Vuoi vedere se un college supera l’altro.

Cosa significa “unidirezionale” o “Bidirezionale?,

unidirezionale o bidirezionale si riferisce al numero di variabili indipendenti (IV) nell’analisi del test di varianza.

unidirezionale ha una variabile indipendente (con 2 livelli). Ad esempio: marca di cereali,
A due vie ha due variabili indipendenti (può avere più livelli). Ad esempio: marca di cereali, calorie.

Che cosa sono “Gruppi” o “Livelli”?

Gruppi o livelli sono gruppi diversi all’interno della stessa variabile indipendente. Nell’esempio precedente, i livelli per “marca di cereali” potrebbero essere portafortuna, crusca di uva passa, cornflakes — un totale di tre livelli., I livelli di “Calorie” potrebbero essere: zuccherato, non zuccherato-un totale di due livelli.

Diciamo che stai studiando se un gruppo di supporto alcolico e una consulenza individuale combinati sono il trattamento più efficace per abbassare il consumo di alcol. Potresti dividere i partecipanti allo studio in tre gruppi o livelli:

Solo farmaci,
Farmaci e consulenza,
Solo consulenza.

La tua variabile dipendente sarebbe il numero di bevande alcoliche consumate al giorno.,

Se i tuoi gruppi o livelli hanno una struttura gerarchica (ogni livello ha sottogruppi univoci), usa un ANOVA nidificato per l’analisi.

Cosa significa” Replica”?

È se stai replicando (cioè duplicando) i tuoi test con più gruppi. Con un ANOVA a due vie con replica, hai due gruppi e gli individui all’interno di quel gruppo stanno facendo più di una cosa (cioè due gruppi di studenti di due college che prendono due test). Se si dispone di un solo gruppo che esegue due test, utilizzare senza replica.

Tipi di test.,

Esistono due tipi principali: unidirezionale e bidirezionale. I test bidirezionali possono essere con o senza replica.

ANOVA unidirezionale tra gruppi: utilizzato quando si desidera testare due gruppi per vedere se c’è una differenza tra loro.
ANOVA bidirezionale senza replica: utilizzato quando si dispone di un gruppo e si esegue il doppio test dello stesso gruppo. Ad esempio, stai testando una serie di individui prima e dopo che prendono un farmaco per vedere se funziona o meno.
ANOVA bidirezionale con replica: due gruppi e i membri di quei gruppi stanno facendo più di una cosa., Ad esempio, due gruppi di pazienti provenienti da diversi ospedali che cercano due terapie diverse.

Torna all’inizio

ANOVA unidirezionale

Un ANOVA unidirezionale viene utilizzato per confrontare due mezzi da due gruppi indipendenti (non correlati) utilizzando la distribuzione F. L’ipotesi nulla per il test è che i due mezzi siano uguali. Pertanto, un risultato significativo significa che i due mezzi sono disuguali.

Esempi di quando utilizzare un ANOVA unidirezionale

Situazione 1: Hai un gruppo di individui suddivisi casualmente in gruppi più piccoli e completando compiti diversi., Ad esempio, potresti studiare gli effetti del tè sulla perdita di peso e formare tre gruppi: tè verde, tè nero e nessun tè.
Situazione 2: Simile alla situazione 1, ma in questo caso gli individui sono divisi in gruppi in base a un attributo che possiedono. Ad esempio, potresti studiare la forza delle gambe delle persone in base al peso. Si potrebbe dividere i partecipanti in categorie di peso (obesi, sovrappeso e normale) e misurare la loro forza delle gambe su una macchina di peso.,

Limitazioni dell’ANOVA unidirezionale

Un ANOVA unidirezionale ti dirà che almeno due gruppi erano diversi l’uno dall’altro. Ma non ti dirà quali gruppi erano diversi. Se il test restituisce una statistica f significativa, potrebbe essere necessario eseguire un test ad hoc (come il test di differenza meno significativo) per dirti esattamente quali gruppi hanno avuto una differenza di mezzi.
Torna all’inizio

ANOVA bidirezionale

Un ANOVA bidirezionale è un’estensione dell’ANOVA a senso unico. Con un modo unidirezionale, hai una variabile indipendente che influenza una variabile dipendente., Con un ANOVA a due vie, ci sono due indipendenti. Usa un ANOVA a due vie quando hai una variabile di misura (cioè una variabile quantitativa) e due variabili nominali. In altre parole, se il tuo esperimento ha un risultato quantitativo e hai due variabili esplicative categoriali, un ANOVA a due vie è appropriato.

Ad esempio, potresti voler scoprire se c’è un’interazione tra reddito e genere per il livello di ansia durante i colloqui di lavoro. Il livello di ansia è il risultato, o la variabile che può essere misurata. Genere e reddito sono le due variabili categoriali., Queste variabili categoriali sono anche le variabili indipendenti, che sono chiamati fattori in un ANOVA bidirezionale.

I fattori possono essere suddivisi in livelli. Nell’esempio precedente, il livello di reddito potrebbe essere suddiviso in tre livelli: basso, medio e alto reddito. Genere potrebbe essere diviso in tre livelli: maschio, femmina, e transgender. I gruppi di trattamento sono tutte le possibili combinazioni dei fattori. In questo esempio ci sarebbero 3 x 3 = 9 gruppi di trattamento.

Effetto principale e effetto di interazione

I risultati di un ANOVA bidirezionale calcoleranno un effetto principale e un effetto di interazione., L’effetto principale è simile a un ANOVA a senso unico: l’effetto di ciascun fattore è considerato separatamente. Con l’effetto di interazione, tutti i fattori sono considerati allo stesso tempo. Gli effetti di interazione tra fattori sono più facili da testare se c’è più di un’osservazione in ogni cellula. Per l’esempio precedente, è possibile inserire più punteggi di stress nelle celle. Se si inseriscono più osservazioni nelle celle, il numero in ogni cella deve essere uguale.

Due ipotesi nulle vengono testate se si sta posizionando un’osservazione in ogni cella., Per questo esempio, quelle ipotesi sarebbero:
H01: Tutti i gruppi di reddito hanno uguale stress medio.
H02: Tutti i gruppi di genere hanno uguale stress medio.

Per osservazioni multiple nelle celle, si verificherebbe anche una terza ipotesi:
H03: I fattori sono indipendenti o l’effetto di interazione non esiste.

Viene calcolata una statistica F per ogni ipotesi che si sta testando.

Ipotesi per ANOVA bidirezionale

La popolazione deve essere vicina a una distribuzione normale.
I campioni devono essere indipendenti.
Le varianze di popolazione devono essere uguali.,
I gruppi devono avere dimensioni del campione uguali.

Torna su

Che cos’è MANOVA?

MANOVA è solo un ANOVA con diverse variabili dipendenti. È simile a molti altri test ed esperimenti in quanto il suo scopo è scoprire se la variabile di risposta (cioè la variabile dipendente) viene modificata manipolando la variabile indipendente. Il test aiuta a rispondere a molte domande di ricerca, tra cui:

Le modifiche alle variabili indipendenti hanno effetti statisticamente significativi sulle variabili dipendenti?
Quali sono le interazioni tra variabili dipendenti?,
Quali sono le interazioni tra variabili indipendenti?

Esempio MANOVA

Supponiamo di voler scoprire se una differenza nei libri di testo ha influenzato i punteggi degli studenti in matematica e scienze. Miglioramenti in matematica e scienza significa che ci sono due variabili dipendenti, quindi una MANOVA è appropriata.

Un ANOVA ti darà un singolo valore f (univariato) mentre un MANOVA ti darà un valore F multivariato. MANOVA verifica le variabili dipendenti multiple creando nuove variabili dipendenti artificiali che massimizzano le differenze di gruppo., Queste nuove variabili dipendenti sono combinazioni lineari delle variabili dipendenti misurate.

Interpretazione dei risultati MANOVA

Se il valore F multivariato indica che il test è statisticamente significativo, ciò significa che qualcosa è significativo. Nell’esempio precedente, non saprai se i punteggi matematici sono migliorati, i punteggi scientifici sono migliorati (o entrambi)., Una volta ottenuto un risultato significativo, è necessario esaminare ogni singolo componente (i test F univariati) per vedere quali variabili dipendenti hanno contribuito al risultato statisticamente significativo.

Vantaggi e svantaggi di MANOVA vs. ANOVA

Vantaggi

MANOVA consente di testare più variabili dipendenti.
MANOVA può proteggere dagli errori di tipo I.

Svantaggi

MANOVA è molte volte più complicato di ANOVA, rendendo una sfida vedere quali variabili indipendenti influenzano le variabili dipendenti.,
Si perde un grado di libertà con l’aggiunta di ogni nuova variabile.
Le variabili dipendenti dovrebbero essere il più possibile non correlate. Se sono correlati, la perdita di gradi di libertà significa che non ci sono molti vantaggi nell’includere più di una variabile dipendente dal test.

Riferimento:
(SFSU)

Torna su

Che cos’è l’ANOVA fattoriale?

Un ANOVA fattoriale è un’analisi del test di varianza con più di una variabile indipendente, o “fattore”. Può anche riferirsi a più di un livello di variabile indipendente., Ad esempio, un esperimento con un gruppo di trattamento e un gruppo di controllo ha un fattore (il trattamento) ma due livelli (il trattamento e il controllo). I termini “a due vie” e” a tre vie ” si riferiscono al numero di fattori o al numero di livelli nel test. ANOVA a quattro vie e sopra sono usati raramente perché i risultati del test sono complessi e difficili da interpretare.

Un ANOVA bidirezionale ha due fattori (variabili indipendenti) e una variabile dipendente. Ad esempio, il tempo trascorso a studiare e la conoscenza preliminare sono fattori che influenzano il modo in cui si esegue un test.,
Un ANOVA a tre vie ha tre fattori (variabili indipendenti) e una variabile dipendente. Ad esempio, il tempo trascorso a studiare, la conoscenza preliminare e le ore di sonno sono fattori che influenzano il modo in cui si esegue un test

L’ANOVA fattoriale è un modo efficace per condurre un test. Invece di eseguire una serie di esperimenti in cui si verifica una variabile indipendente contro una variabile dipendente, è possibile testare tutte le variabili indipendenti allo stesso tempo.

Variabilità

In un ANOVA unidirezionale, la variabilità è dovuta alle differenze tra i gruppi e alle differenze all’interno dei gruppi., Nell’ANOVA fattoriale, ogni livello e fattore sono accoppiati l’uno con l’altro (”incrociati”). Questo ti aiuta a vedere quali interazioni stanno succedendo tra i livelli e i fattori. Se c’è un’interazione, le differenze in un fattore dipendono dalle differenze in un altro.

Diciamo che stavi eseguendo un ANOVA a due vie per testare le prestazioni maschili / femminili in un esame finale. I soggetti avevano avuto 4, 6 o 8 ore di sonno.,

IV1: SESSO (maschio/femmina)
IV2: SONNO (4/6/8)
DV: Punteggio dell’esame finale

Un ANOVA fattoriale bidirezionale ti aiuterà a rispondere alle seguenti domande:

Il sesso è un effetto principale? In altre parole, gli uomini e le donne differiscono in modo significativo sulle loro prestazioni di esame?
Il sonno è un effetto principale? In altre parole, le persone che hanno avuto 4,6 o 8 ore di sonno differiscono significativamente nelle loro prestazioni?
Esiste un’interazione significativa tra i fattori? In altre parole, come interagiscono ore di sonno e sesso per quanto riguarda le prestazioni dell’esame?,
Si possono trovare differenze nel sesso e nelle prestazioni degli esami nei diversi livelli di sonno?

Ipotesi di ANOVA fattoriale

Normalità: la variabile dipendente è normalmente distribuita.
Indipendenza: Osservazioni e gruppi sono indipendenti l’uno dall’altro.
Uguaglianza di varianza: le varianze della popolazione sono uguali tra fattori / livelli.

Come eseguire un ANOVA

Questi test richiedono molto tempo a mano. In quasi tutti i casi ti consigliamo di utilizzare il software., Ad esempio, in Excel sono disponibili diverse opzioni:

ANOVA bidirezionale in Excel con replica e senza replica.
Un modo ANOVA in Excel 2013.

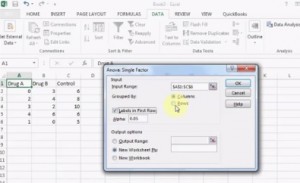
Esecuzione del test in Excel.

I test ANOVA nei pacchetti di statistiche vengono eseguiti su dati parametrici. Se hai dati di rango o ordinati, ti consigliamo di eseguire un ANOVA non parametrico (di solito si trova sotto una voce diversa nel software, come “test non parametrici”).,

Passi

È improbabile che tu voglia fare questo test a mano, ma se devi, questi sono i passi che vorrai fare:

Trova la media per ciascuno dei gruppi.
Trova la media complessiva (la media dei gruppi combinati).
Trova la variazione all’interno del gruppo; la deviazione totale del punteggio di ciascun membro dalla media del gruppo.
Trova la variazione tra gruppi: la deviazione di ogni media di gruppo dalla media complessiva.
Trova la statistica F: il rapporto tra la variazione del gruppo e la variazione del gruppo.

ANOVA vs., T Test

Il t-test di uno studente ti dirà se c’è una variazione significativa tra i gruppi. Un t-test confronta i mezzi, mentre l’ANOVA confronta le varianze tra le popolazioni.
Si potrebbe tecnicamente eseguire una serie di t-test sui dati. Tuttavia, man mano che i gruppi crescono di numero, potresti finire con molti confronti di coppia che devi eseguire. ANOVA ti darà un singolo numero (la statistica f) e un valore p per aiutarti a supportare o rifiutare l’ipotesi nulla.,
Torna all’inizio

Misure ripetute ANOVA

A misure ripetute ANOVA è quasi la stessa di ANOVA a senso unico, con una differenza principale: si testano gruppi correlati, non quelli indipendenti. Si chiama Misure ripetute perché lo stesso gruppo di partecipanti viene misurato più e più volte. Ad esempio, potresti studiare i livelli di colesterolo dello stesso gruppo di pazienti a 1, 3 e 6 mesi dopo aver cambiato la loro dieta. Per questo esempio, la variabile indipendente è ” tempo “e la variabile dipendente è” colesterolo.,”La variabile indipendente è solitamente chiamata fattore all’interno dei soggetti.

Misure ripetute ANOVA è simile a un semplice disegno multivariato. In entrambi i test, gli stessi partecipanti vengono misurati più e più volte. Tuttavia, con misure ripetute la stessa caratteristica viene misurata con una condizione diversa. Ad esempio, la pressione sanguigna viene misurata sulla condizione “tempo”. Per un semplice design multivariato è la caratteristica che cambia. Ad esempio, è possibile misurare la pressione sanguigna, la frequenza cardiaca e la frequenza respiratoria nel tempo.,

Motivi per utilizzare misure ripetute ANOVA

Quando si raccolgono dati dagli stessi partecipanti per un periodo di tempo, le differenze individuali (una fonte di differenze tra gruppi) vengono ridotte o eliminate.
Il test è più potente perché la dimensione del campione non è divisa tra i gruppi.
Il test può essere economico, poiché stai usando gli stessi partecipanti.,

Ipotesi per misure ripetute ANOVA

I risultati delle tue misure ripetute ANOVA saranno validi solo se le seguenti ipotesi non sono state violate:

Ci deve essere una variabile indipendente e una variabile dipendente.
La variabile dipendente deve essere una variabile continua, su una scala di intervallo o una scala di rapporto.
La variabile indipendente deve essere categorica, sulla scala nominale o sulla scala ordinale.
Idealmente, i livelli di dipendenza tra coppie di gruppi sono uguali (”sfericità”)., Le correzioni sono possibili se questa ipotesi viene violata.

Misure ripetute ANOVA in SPSS: Passi

Passo 1: Fare clic su “Analizza”, quindi passare il mouse su ” Modello lineare generale.”Fare clic su” Misure ripetute.”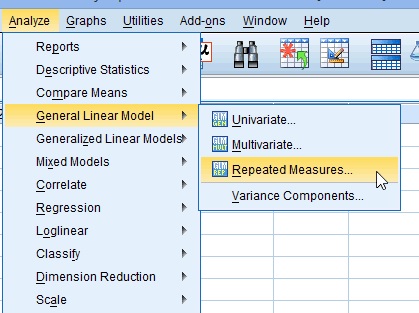

Passo 2: Sostituisci il nome” factor1 ” con qualcosa che rappresenti la tua variabile indipendente. Ad esempio, potresti mettere “età” o “tempo.”

Passo 3: Inserire il “Numero di livelli.”Questo è il numero di volte in cui è stata misurata la variabile dipendente. Ad esempio, se hai preso misure ogni settimana per un totale di 4 settimane, questo numero sarebbe 4.,

Passo 4: Fai clic sul pulsante “Aggiungi” e quindi assegna un nome alla variabile dipendente.

Passo 5: Fare clic sul pulsante” Aggiungi”. Verrà visualizzata una casella Definizione misure ripetute. Fare clic sul pulsante “Definisci”.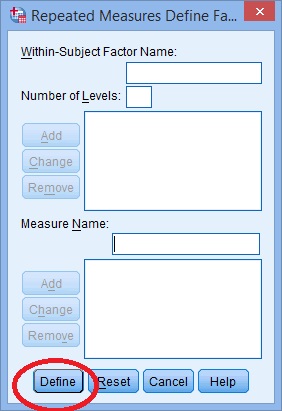

Passo 6: Utilizzare i tasti freccia per spostare il vostro variabili da sinistra a destra in modo che la vostra schermata simile all’immagine qui sotto: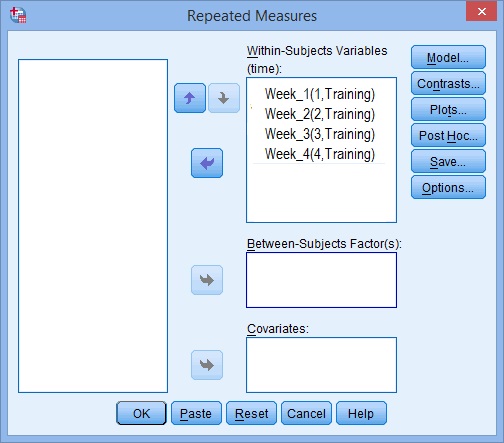

Passo 7: fare Clic su “Trame” e utilizzare i tasti freccia per trasferire il fattore dalla casella di sinistra sull’Asse Orizzontale di dialogo.

Passo 8: Fai clic su “Aggiungi” e quindi su “Continua” nella parte inferiore della finestra.,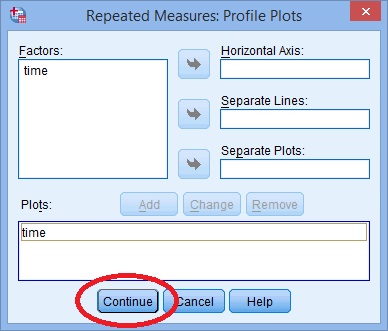

Passo 9: Fare clic su “Opzioni”, quindi trasferire i fattori dalla casella di sinistra al display Significa per la casella a destra.

Passo 10: Fare clic sulle seguenti caselle di controllo:

Confronta gli effetti principali.
Statistiche descrittive.
Stime della dimensione dell’effetto.

Passo 11: Selezionare “Bonferroni” dal menu a discesa in Regolazione intervallo di confidenza.
Passo 12: Fare clic su “Continua” e quindi fare clic su ” OK ” per eseguire il test.,
Torna su

Sphericità

In statistica, sphericità (ε) si riferisce al test di sfericità di Mauchly, che è stato sviluppato nel 1940 da John W. Mauchly, che ha co-sviluppato il primo computer elettronico per uso generale.

Definizione

La sfericità viene utilizzata come ipotesi nelle misure ripetute ANOVA. L’ipotesi afferma che le varianze delle differenze tra tutte le possibili coppie di gruppi sono uguali. Se i tuoi dati violano questa ipotesi, può comportare un aumento di un errore di tipo I (il rifiuto errato dell’ipotesi nulla).,

È molto comune che le misure ripetute di ANOVA comportino una violazione dell’ipotesi. Se l’ipotesi è stata violata, sono state sviluppate correzioni che possono evitare aumenti del tasso di errore di tipo I. La correzione viene applicata ai gradi di libertà nella distribuzione F.

Test di sfericità di Mauchly

Il test di Mauchly per sfericità può essere eseguito nella maggior parte dei software statistici, dove tende ad essere il test predefinito per sfericità. Il test di Mauchly è ideale per campioni di medie dimensioni., Potrebbe non riuscire a rilevare la sfericità in piccoli campioni e potrebbe rilevare eccessivamente in campioni di grandi dimensioni.
Se il test restituisce un piccolo valore p (p≤.05), questa è un’indicazione che i tuoi dati hanno violato l’ipotesi. La seguente immagine dell’output SPSS per ANOVA mostra che il significato “sig” collegato a Mauchly è .274. Ciò significa che l’ipotesi non è stata violata per questo insieme di dati.

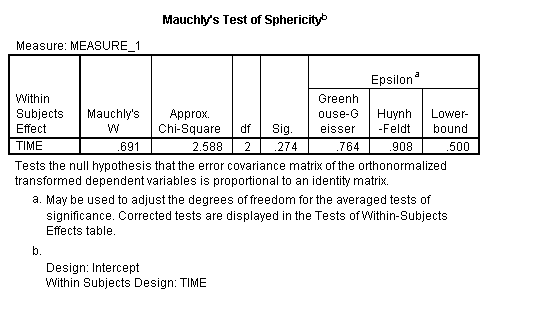
Immagine: UVM.,EDU

Riporteresti il risultato di cui sopra come “Il test di Mauchly indicava che l’assunzione di sfericità non era stata violata, χ2(2) = 2.588, p = .274.”

Se il test ha restituito un piccolo valore p, è necessario applicare una correzione, di solito la correzione:

Greehouse-Geisser.
Correzione di Huynh-Feldt.

Quando ε ≤ 0.75 (o non si sa quale sia il valore per la statistica), utilizzare la correzione Serra-Geisser.
Quando ε >.75, utilizzare la correzione Huynh-Feldt.,