Contenuto
funzioni di densità di Probabilità
La funzione di densità di probabilità (pdf) \(f(x)\) di una variabile casuale continua \(X\) è definita come la derivata della cdf \(F(x)\):
\
a volte è utile considerare il cdf \(F(x)\) in termini di il pdf \(f(x)\):
\
Il pdf \(f(x)\) ha due caratteristiche importanti:
- \(f(x) \geq 0\) per ogni \(x\)
- \(\displaystyle\int_{-\infty}^{\infty} f(x)\;dx = 1\).,
Una varietà infinita di forme è possibile per un pdf, poiché gli unici requisiti sono le due proprietà sopra. Il pdf può avere uno o più picchi, o nessun picco a tutti; può avere discontinuità, essere costituito da combinazioni di funzioni, e così via. la figura 5 mostra un pdf con un singolo picco e una leggera asimmetria. Come nel caso di un tipico pdf, il valore della funzione si avvicina a zero come \(x \ to \ infty\) e \(x \to -\infty\).
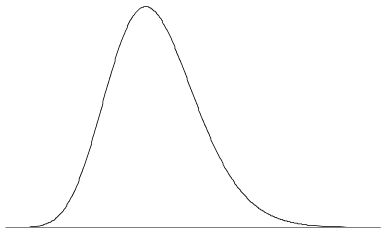
Figura 5: Un pdf può essere simile a questo.,
Ora esploriamo come le probabilità riguardanti la variabile casuale continua \(X\) si riferiscono al suo pdf. Il risultato importante qui è che
\_a^b.\]
Questo risultato deriva dal fatto che entrambi i lati sono uguali a \(F(b) – F(a)\).
Note.
- Per una variabile casuale continua, dobbiamo considerare la probabilità che si trovi in un intervallo. L’importanza di questo risultato è che ci dice che, per trovare la probabilità, dobbiamo trovare l’area sotto il pdf sull’intervallo dato.
- L’area totale sotto il pdf è uguale a 1., Quindi questo risultato ci dice che, per approssimare la probabilità che la variabile casuale si trovi in un dato intervallo, dobbiamo solo indovinare la frazione dell’area sotto il pdf tra le estremità dell’intervallo.
- Questo risultato fornisce un’altra prospettiva sul perché i pdf non possono essere negativi, poiché se lo fossero, si potrebbe ottenere una probabilità negativa, il che è impossibile.
- Il pdf è analogo, ma diverso, alla funzione di probabilità (pf) per una variabile casuale discreta. Un pf dà una probabilità, quindi non può essere maggiore di uno., Un pdf \ (f (x)\), tuttavia, può dare un valore maggiore di uno per alcuni valori di \(x\), poiché non è il valore di \(f(x)\) ma l’area sotto la curva che rappresenta la probabilità. D’altra parte, l’altezza della curva riflette la probabilità relativa. Se \(f(b) = 2f(a)\), allora un’osservazione vicino a \(b\) è approssimativamente due volte più probabile di un’osservazione vicino a \(a\).,
pagina Successiva – Contenuto – Media e varianza di una variabile casuale continua
 |
Questa pubblicazione è finanziato dalla Governo Australiano Dipartimento dell’Educazione, per l’Occupazione e Rapporti sul Lavoro |
Collaboratori Termine di utilizzo |