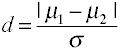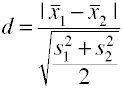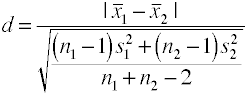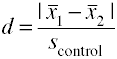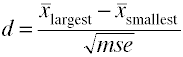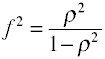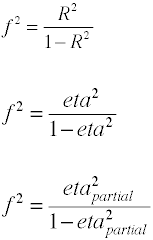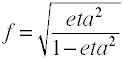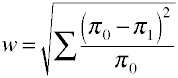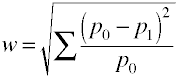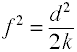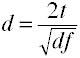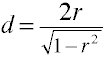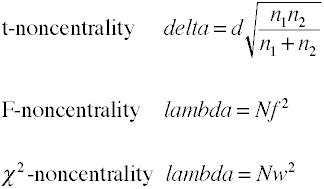Un uso di effect-size è un indice standardizzato indipendente dalla dimensione del campione e quantifica l’entità della differenza tra le popolazioni o la relazione tra le variabili esplicative e di risposta. Un altro uso della dimensione dell’effetto è il suo uso nell’eseguimentoanalisi della potenza.
Dimensione dell’effetto per differenza di mezzi
Dimensione dell’effetto per differenze di mezzi è dato d di Cohen è definito in termini di mezzi di popolazione (µs) e una popolazione standarddeviation (σ), come mostrato di seguito.,
Ci sono diversi modi in cui si potrebbe stimare σ da dati di esempio che portano a più varianti all’interno della famiglia d di Cohen.
Usando la radice quadrata media deviazione standard
Utilizzando il pool di deviazione standard (Siepi’ g)
Questa versione di Cohen d utilizza il pool di deviazione standard ed è anche conosciuto come Siepi’ g.,
È possibile ottenere facilmente questo valore da un programma anova prendendo la radice quadrata dell’errore meansquare che è anche noto come errore quadrato medio radice.
Utilizzando la deviazione standard del gruppo di controllo (Glass ‘ Δ)
Un’altra versione della d di Cohen che utilizza la deviazione standard per il gruppo di controllo è anche nota come Glass’ Δ.,
Più di due gruppi
Quando ci sono più di due gruppi di utilizzare la differenza tra il più grande e smallestmeans diviso per la radice quadrata dell’errore quadratico medio.
dimensione dell’Effetto per F-i rapporti di analisi di regressione
Per la regressione OLS, la misura degli effetti di dimensione F definita da Cohen come segue.,
Ancora una volta ci sono diversi modi in cui la dimensione dell’effetto può essere calcolata dai dati di esempio. Notache η2 è un altro nome per R2.
dimensione dell’Effetto per F-i rapporti di analisi della varianza
La dimensione dell’effetto utilizzati nell’analisi della varianza è definito dal rapporto tra la popolazione di standarddeviations.,
Sebbene la f di Cohen sia definita come sopra, di solito viene calcolata prendendo la radice quadrata di f2.
Dimensione dell’effetto per χ2 dalle tabelle di contingenza
Ancora una volta iniziamo con la formula definizionale in termini di valori di popolazione.La dimensione dell’effetto w è la radice quadrata della statistica chi-quadrata standardizzata.,
Ed ecco come w viene calcolato utilizzando i dati di esempio.
Ecco una tabella dei valori suggeriti per effetti bassi, medi e alti (Cohen, 1988). Questi valori non dovrebbero essere presi come assoluti e dovrebbero essere interpretati nel contesto del tuo programma di ricerca. I valori per i grandi effetti sono spesso superati nella pratica con valori d di Cohen superiori a 1.0 non rari.,Tuttavia, utilizzando molto grandi dimensioni effetto in analisi di potenza prospettica probabilmente non è una buona idea asit potrebbe portare a studi sotto alimentato.,formule
dove k = numero di gruppi
Converti t a d per due gruppi indipendenti
la Conversione r a d per due gruppi indipendenti
Noncentrality stime
Analisi della potenza utilizzando metodi analitici di richiedere un preventivo di noncentrality che è basicallythe dimensione dell’effetto moltiplicato per la dimensione del campione fattore., Ecco alcune formule per stimare la noncentralità.
Esempio di analisi della potenza
Ecco un esempio che riunisce la dimensione dell’effetto e la non centralità in un’analisi della potenza.
Considera un’analisi unidirezionale della varianza con tre gruppi (k = 3). Se ci aspettiamo che andeta2 sia uguale .,12 nel qual caso la dimensione dell’effetto sarà
effect size f = sqrt(eta2/(1-eta2)) = sqrt(.12/(1-.12)) = .369
Con una dimensione del campione proiettata di 60 la stima della noncentralità è
noncentrality coefficient lambda = N*f = 60*.369^2 = 60*.136 = 8.17
Il numeratore gradi di libertà è k-1 = 3-1 = 2 mentre il denominatore df è N-k = 60-3 = 57.Il valore critico di F con 2 e 57 gradi di libertà è 3.16. Che si traduce in una potenza di
power = noncentralFtail(df1,df2,lambda,Fcrit(2,57)) = noncentralFtail(2,57,8.17,3.16) = .703
quindi, un N di 60 e la dimensione dell’effetto di.369 produce una potenza proiettata di circa .7.
Siamo in grado di migliorare la potenza di .7 utilizzando una dimensione del campione proiettata di 75 invece di 60., Con la stessa dimensione effetto di.369, otteniamo una nuova stima di non centralità di
noncentrality coefficient lambda = N*f = 75*.369^2 = 75*.136 = 10.2
I gradi di libertà del numeratore rimangono gli stessi mentre il denominatore df ora è uguale N-k = 75-3 = 72.Il valore critico di F con 2 e 72 gradi di libertà di 3.12. Questa volta la potenza è
power = noncentralFtail(df1,df2,lambda,Fcrit(2,72)) = noncentralFtail(2,72,10.2,3.12) = .807
che è entro limiti di ricerca accettabili.
Si noti che diversi pacchetti stat utilizzano nomi diversi e un diverso ordine di argomenti nella funzione che abbiamo chiamato noncentralFtail. Dovrai leggere la documentazioneviene fornito con il tuo software.,
Becker, L. Psicologia 590 note del corso. Ho visto 19 Jun 2009 <http://web.uccs.edu/lbecker/Psy590/es.htm>
Cohen, J. 1988. Analisi di potenza statistica per le scienze comportamentali. Home Page-Comune di Milano