Il coefficiente α è la procedura più utilizzata per stimare l’affidabilità nella ricerca applicata. Come affermato da Sijtsma (2009), la sua popolarità è tale che Cronbach (1951) è stato citato come riferimento più frequentemente dell’articolo sulla scoperta della doppia elica del DNA., Tuttavia, i suoi limiti sono ben noti (Lord and Novick, 1968; Cortina, 1993; Yang and Green, 2011), alcuni dei più importanti sono le ipotesi di errori non correlati, tau-equivalenza e normalità.
L’assunzione di incorrelati errori (errore punteggio di ogni coppia di elementi è incorrelate) è un’ipotesi Classica Prova di Teoria (Signore e Novick, 1968), la cui violazione può comportare la presenza di complesse strutture multidimensionali che richiedono procedure di stima che prendere in considerazione tale complessità (ad esempio, Tarkkonen e Vehkalahti, 2005; Verde e Yang, 2015)., È importante sradicare l’errata convinzione che il coefficiente α sia un buon indicatore di unidimensionalità perché il suo valore sarebbe più alto se la scala fosse unidimensionale. In realtà è esattamente il contrario, come è stato dimostrato da Sijtsma (2009), e la sua applicazione in tali condizioni può portare a sopravvalutare fortemente l’affidabilità (Raykov, 2001). Di conseguenza, prima di calcolare α è necessario verificare che i dati si adattino a modelli unidimensionali.
L’assunzione di tau-equivalenza (cioè,, lo stesso punteggio vero per tutti gli elementi di prova, o carichi di fattori uguali di tutti gli elementi in un modello fattoriale) è un requisito per α essere equivalente al coefficiente di affidabilità (Cronbach, 1951). Se l’assunzione di tau-equivalenza viene violata, il vero valore di affidabilità verrà sottovalutato (Raykov, 1997; Graham, 2006) di un importo che può variare tra lo 0,6 e l ‘ 11,1% a seconda della gravità della violazione (Green e Yang, 2009a). Lavorare con dati conformi a questa ipotesi non è generalmente praticabile nella pratica( Teo e Fan, 2013); il modello congenerico (cioè,, loadings di fattore diverso) è il più realistico.
Il requisito della normalità multivariante è meno noto e influenza sia la stima dell’affidabilità puntuale che la possibilità di stabilire intervalli di confidenza (Dunn et al., 2014). Sheng e Sheng (2012) hanno osservato di recente che quando le distribuzioni sono distorte e/o leptokurtiche, viene prodotto un bias negativo quando viene calcolato il coefficiente α; risultati simili sono stati presentati da Green e Yang (2009b) in un’analisi degli effetti delle distribuzioni non normali nella stima dell’affidabilità., Lo studio dei problemi di asimmetria è più importante quando vediamo che in pratica i ricercatori lavorano abitualmente con scale distorte (Micceri, 1989; Norton et al., 2013; Ho e Yu, 2014). Ad esempio, Micceri (1989) ha stimato che circa 2/3 dell’abilità e oltre 4/5 delle misure psicometriche mostravano un’asimmetria almeno moderata (cioè un’asimmetria intorno a 1). Nonostante ciò, l’impatto dell’asimmetria sulla stima dell’affidabilità è stato poco studiato.,
Considerando l’abbondante letteratura sulle limitazioni e i pregiudizi del coefficiente α (Revelle e Zinbarg, 2009; Sijtsma, 2009, 2012; Cho e Kim, 2015; Sijtsma e van der Ark, 2015), sorge la domanda sul perché i ricercatori continuino a usare α quando esistono coefficienti alternativi che superano queste limitazioni. È possibile che l’eccesso di procedure per la stima dell’affidabilità sviluppato nel secolo scorso abbia oscurato il dibattito. Ciò sarebbe stato ulteriormente aggravato dalla semplicità di calcolo di questo coefficiente e dalla sua disponibilità nei software commerciali.,
La difficoltà di stimare il coefficiente di affidabilità pxx risiede nella sua definizione pxx’=σt2 σ σx2, che include il punteggio vero nel numeratore di varianza quando questo è per natura inosservabile. Il coefficiente α cerca di approssimare questa varianza non osservabile dalla covarianza tra gli elementi o i componenti. Cronbach (1951) ha mostrato che in assenza di tau-equivalenza, il coefficiente α (o lambda di Guttman 3, che è equivalente a α) era una buona approssimazione del limite inferiore., Così, quando le ipotesi sono violati, il problema si traduce nel trovare le migliori limite inferiore; infatti questo viene dato il nome al più Grande dei minoranti metodo (GLB), che costituisce la migliore approssimazione da un teorico angolo (Jackson e Agunwamba, 1977; Woodhouse e Jackson, 1977; Shapiro e ten Berge, 2000; Sočan, 2000; ten Berge e Sočan, 2004; Sijtsma, 2009). Tuttavia, Revelle e Zinbarg (2009) ritengono che ω dia un limite inferiore migliore di GLB., C’è quindi un dibattito irrisolto su quale di questi due metodi dia il miglior limite inferiore; inoltre la questione della non-normalità non è stata esaminata in modo esaustivo, come discute il presente lavoro.
ω Coefficienti
McDonald (1999) ha proposto il wt coefficiente per la stima dell’affidabilità di un’analisi fattoriale quadro, che può essere espressa formalmente come:
Dove λ j è il caricamento dell’elemento j, λj2 è la comunanza di elemento j e ψ equivale all’unicità., Il coefficiente wt, includendo i lambda nelle sue formule, è adatto sia quando esiste l’equivalenza tau (cioè, carichi di fattori uguali di tutti gli elementi di prova) (wt coincide matematicamente con α), sia quando elementi con diverse discriminazioni sono presenti nella rappresentazione del costrutto (cioè, carichi di fattori diversi degli elementi: misure congeneriche). Di conseguenza wt corregge il bias di sottostima di α quando l’assunzione di tau-equivalenza viene violata (Dunn et al., 2014) e diversi studi dimostrano che è una delle migliori alternative per stimare l’affidabilità (Zinbarg et al.,, 2005, 2006; Revelle e Zinbarg, 2009), anche se ad oggi il suo funzionamento in condizioni di asimmetria è sconosciuto.
Quando esiste correlazione tra errori, o c’è più di una dimensione latente nei dati, il contributo di ogni dimensione per la varianza totale spiegata è stimato, ottenendo il cosiddetto gerarchica ω (wh) che ci permette di correggere il peggiore sovrastima bias di α con dati multidimensionali (vedi Tarkkonen e Vehkalahti, 2005; Zinbarg et al., 2005; Revelle e Zinbarg, 2009)., I coefficienti wh e wt sono equivalenti nei dati unidimensionali, quindi ci riferiremo a questo coefficiente semplicemente come ω.
Greatest Lower Bound (GLB)
Sijtsma (2009) mostra in una serie di studi che uno dei più potenti stimatori di affidabilità è GLB—dedotto da Woodhouse e Jackson (1977) dalle ipotesi della Teoria dei test classica (Cx = Ct + Ce)—una matrice di covarianza inter-item per i punteggi degli oggetti osservati Cx. Si suddivide in due parti: la somma della matrice di covarianza tra elementi per i punteggi veri dell’elemento Ct; e la matrice di covarianza degli errori tra elementi Ce (ten Berge e Sočan, 2004)., La sua espressione è:
dove σx2 è la varianza di prova e tr (Ce) si riferisce alla traccia della matrice di covarianza degli errori inter-item che si è dimostrata così difficile da stimare. Una soluzione è stata quella di utilizzare procedure fattoriali come l’analisi del fattore di rango minimo (una procedura nota come glb.fa). Più recentemente la procedura GLB algebrica (GLBa) è stata sviluppata da un algoritmo ideato da Andreas Moltner (Moltner e Revelle, 2015)., Secondo Revelle (2015a) questa procedura adotta la forma che è più fedele alla definizione originale di Jackson e Agunwamba (1977), e ha il vantaggio aggiunto di introdurre un vettore per pesare gli elementi per importanza (Al-Homidan, 2008).
Nonostante i suoi punti di forza teorici, GLB è stato molto poco utilizzato, anche se alcuni recenti studi empirici hanno dimostrato che questo coefficiente produce risultati migliori di α (Lila et al., 2014) e α e ω (Wilcox et al., 2014)., Tuttavia, in piccoli campioni, sotto l’assunto della normalità, tende a sopravvalutare il vero valore di affidabilità (Shapiro e ten Berge, 2000); tuttavia il suo funzionamento in condizioni non normali rimane sconosciuto, in particolare quando le distribuzioni degli elementi sono asimmetriche.
Considerando i coefficienti sopra definiti, e i pregiudizi e i limiti di ciascuno, lo scopo di questo lavoro è valutare la robustezza di questi coefficienti in presenza di elementi asimmetrici, considerando anche l’assunzione di tau-equivalenza e la dimensione del campione.,
Metodi
la Generazione di Dati
I dati sono stati generati utilizzando R (R Development Core Team, 2013) e RStudio (Racine, 2012) software, seguendo il modello fattoriale:
dove Xij è simulata la risposta del soggetto al punto j, λjk è il caricamento dell’elemento j nel Fattore k (che è stato generato dal unifactorial modello); Fk è il fattore latente generato da una distribuzione normale standardizzata (media 0 e varianza 1), e non è casuale errore di misura di ogni elemento, anche a seguito di una distribuzione normale standardizzata.,
Inclinata elementi: normale Standard Xij sono stati trasformati per generare distribuzioni non normali utilizzando la procedura proposta da Headrick (2002) l’applicazione di un quinto ordine polinomiale trasforma:
Condizioni Simulate
Per valutare le prestazioni dei coefficienti di affidabilità (α, ω, GLB e GLBa) abbiamo lavorato con tre dimensioni del campione (250, 500, 1000), due grandezze di prova: breve (6 elementi) e lungo (12 elementi), due condizioni di tau-equivalenza (di cui uno con tau-equivalenza e uno senza, cioè,, congeneric) e l’incorporazione progressiva di articoli asimmetrici (da tutti gli articoli che sono normali a tutti gli articoli che sono asimmetrici). Nel test breve l’affidabilità è stata impostata a 0,731, che in presenza di tau-equivalenza si ottiene con sei elementi con carichi di fattore = 0,558; mentre il modello congenerico si ottiene impostando carichi di fattore a valori di 0.3, 0.4, 0.5, 0.6, 0.7, e 0.8 (vedi Appendice I). Nel lungo test di 12 elementi l’affidabilità è stata impostata su 0.,845 prendendo gli stessi valori del test breve sia per l’equivalenza tau che per il modello congenerico (in questo caso c’erano due elementi per ogni valore di lambda). In questo modo sono state simulate 120 condizioni con 1000 repliche in ogni caso.
Analisi dei dati
Le analisi principali sono state effettuate utilizzando i pacchetti Psych (Revelle, 2015b) e GPArotation (Bernaards e Jennrich, 2015), che consentono di stimare α e ω. Due approcci computerizzati sono stati utilizzati per stimare GLB: glb.fa (Revelle, 2015a) e glb.,algebraic (Moltner e Revelle, 2015), quest’ultimo lavorato da autori come Hunt e Bentler (2015).
Al fine di valutare l’accuratezza dei vari stimatori nel recupero dell’affidabilità, abbiamo calcolato il Quadrato Medio Radice dell’errore (RMSE) e il bias. La prima è la media delle differenze tra l’affidabilità stimata e quella simulata ed è formalizzata come:
dove ρ^ è l’affidabilità stimata per ciascun coefficiente, ρ l’affidabilità simulata e Nr il numero di repliche., L’ % bias è inteso come la differenza tra la media delle stime di affidabilità e la simulazione di affidabilità ed è definito come:
In entrambi gli indici, maggiore è il valore, maggiore è l’imprecisione della stima, ma a differenza di RMSE, il bias può essere positivo o negativo; in questo caso ulteriori informazioni sarebbe ottenuto se il coefficiente è di sottovalutare o sopravvalutare la simulazione di un parametro di affidabilità., In seguito alla raccomandazione di Hoogland e Boomsma (1998) i valori di RMSE < 0,05 e % bias < 5% sono stati considerati accettabili.
Risultati
I risultati principali sono riportati nella Tabella 1 (6 elementi) e nella Tabella 2 (12 elementi). Questi mostrano il bias RMSE e % dei coefficienti in tau-equivalenza e condizioni congeneriche, e come l’asimmetria della distribuzione del test aumenta con l’incorporazione graduale di elementi asimmetrici.
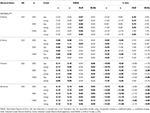
Tabella 1., RMSE e Bias con tau-equivalenza e condizione congenerica per 6 articoli, tre dimensioni del campione e il numero di articoli inclinati.
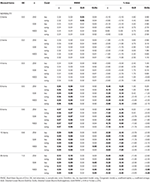
Tabella 2. RMSE e Bias con tau-equivalenza e condizione congenerica per 12 articoli, tre dimensioni del campione e il numero di articoli inclinati.
Solo in condizioni di tau-equivalenza e normalità (skewness< 0.2) si osserva che il coefficiente α stima correttamente l’affidabilità simulata, come ω., Nella condizione congenerica ω corregge la sottostima di α. Sia GLB che GLBa presentano un bias positivo sotto la normalità, tuttavia GLBa mostra approssimativamente ½ meno % di bias rispetto a GLB (vedere Tabella 1). Se consideriamo la dimensione del campione, osserviamo che all’aumentare della dimensione del test, il bias positivo di GLB e GLBa diminuisce, ma non scompare mai.
In condizioni asimmetriche, vediamo nella Tabella 1 che sia α che ω presentano una prestazione inaccettabile con RMSE crescente e sottostime che possono raggiungere bias> 13% per il coefficiente α (tra 1 e 2% inferiore per ω)., I coefficienti GLB e GLBa presentano un RMSE inferiore quando aumenta l’asimmetria del test o il numero di elementi asimmetrici (vedere Tabelle 1, 2). Il coefficiente GLB presenta stime migliori quando il valore di skewness del test è di circa 0,30; GLBa è molto simile, presentando stime migliori di ω con un valore di skewness del test intorno a 0,20 o 0,30. Tuttavia, quando il valore di asimmetria aumenta a 0,50 o 0,60, GLB presenta prestazioni migliori rispetto a GLBa. La dimensione della prova (6 o 12 elementi) ha un effetto molto più importante della dimensione del campione sull’accuratezza delle stime.,
Discussione
In questo studio quattro fattori sono stati manipolati: tau-equivalenza o congenerica modello, la dimensione del campione (250, 500, 1000), il numero di elementi di prova (6 e 12) e il numero di asimmetrico articoli (da 0 asimmetrico articoli per tutti gli articoli che vengono asimmetrica) al fine di valutare la robustezza della presenza di asimmetrico dati in quattro affidabilità coefficienti analizzati. Questi risultati sono discussi di seguito.,
In condizioni di tau-equivalenza, i coefficienti α e ω convergono, tuttavia in assenza di tau-equivalenza (congenerica), ω presenta sempre stime migliori e meno RMSE e % bias di α. In questa condizione più realistica quindi (Green e Yang, 2009a; Yang e Green, 2011), α diventa uno stimatore di affidabilità negativamente polarizzato (Graham, 2006; Sijtsma, 2009; Cho e Kim, 2015) e ω è sempre preferibile a α (Dunn et al., 2014). Nel caso di non violazione dell’assunzione di normalità, ω è il miglior stimatore di tutti i coefficienti valutati (Revelle e Zinbarg, 2009).,
Passando alla dimensione del campione, osserviamo che questo fattore ha un piccolo effetto sotto la normalità o un leggero allontanamento dalla normalità: l’RMSE e il bias diminuiscono all’aumentare della dimensione del campione. Tuttavia, si può dire che per questi due coefficienti, con dimensione del campione di 250 e normalità otteniamo stime relativamente accurate (Tang e Cui, 2012; Javali et al., 2011)., Per i coefficienti GLB e GLBa, man mano che la dimensione del campione aumenta l’RMSE e il bias tendono a diminuire; tuttavia mantengono un bias positivo per la condizione di normalità anche con campioni di grandi dimensioni di 1000 (Shapiro e ten Berge, 2000; ten Berge e Sočan, 2004; Sijtsma, 2009).
Per la dimensione del test osserviamo generalmente un RMSE e un bias più alti con 6 elementi rispetto a 12, suggerendo che maggiore è il numero di elementi, minore è il RMSE e il bias degli stimatori (Cortina, 1993). In generale la tendenza è mantenuta sia per 6 che per 12 articoli.,
Quando osserviamo l’effetto di incorporare progressivamente elementi asimmetrici nel set di dati, osserviamo che il coefficiente α è altamente sensibile agli elementi asimmetrici; questi risultati sono simili a quelli trovati da Sheng e Sheng (2012) e Green e Yang (2009b). Il coefficiente ω presenta valori RMSE e bias simili a quelli di α, ma leggermente migliori, anche con l’equivalenza tau. Si scopre che GLB e GLBa presentano stime migliori quando l’asimmetria del test parte da valori vicini a 0.
Considerando che in pratica è comune trovare dati asimmetrici (Micceri, 1989; Norton et al.,, 2013; Ho e Yu, 2014), il suggerimento di Sijtsma (2009) di utilizzare GLB come stimatore di affidabilità sembra ben fondato. Altri autori, come Revelle e Zinbarg (2009) e Green e Yang (2009a), raccomandano l’uso di ω, tuttavia questo coefficiente ha prodotto solo buoni risultati in condizioni di normalità o con una bassa percentuale di elementi di asimmetria. In ogni caso, questi coefficienti presentavano maggiori vantaggi teorici ed empirici rispetto a α. Tuttavia, raccomandiamo ai ricercatori di studiare non solo stime puntuali ma anche di utilizzare la stima dell’intervallo (Dunn et al., 2014).,
Questi risultati sono limitati alle condizioni simulate e si presume che non vi sia alcuna correlazione tra errori. Ciò renderebbe necessario effettuare ulteriori ricerche per valutare il funzionamento dei vari coefficienti di affidabilità con strutture multidimensionali più complesse (Reise, 2012; Green e Yang, 2015) e in presenza di dati ordinali e/o categorici in cui la non conformità con l’assunzione di normalità è la norma.
Conclusione
Quando i punteggi totali dei test sono normalmente distribuiti (es.,, tutti gli articoli sono normalmente distribuiti) ω dovrebbe essere la prima scelta, seguita da α, poiché evitano i problemi di sovrastima presentati da GLB. Tuttavia, quando c’è un’asimmetria di prova bassa o moderata, GLBa deve essere usato. GLB è raccomandato quando la proporzione di elementi asimmetrici è elevata, poiché in queste condizioni l’uso di α e ω come stimatori di affidabilità non è consigliabile, indipendentemente dalla dimensione del campione.
Contributi dell’autore
Sviluppo dell’idea di ricerca e quadro teorico (IT, JA). Costruzione del quadro metodologico (IT, JA)., Sviluppo della sintassi del linguaggio R (IT, JA). Analisi dei dati e interpretazione dei dati (IT, JA). Discussione dei risultati alla luce dell’attuale background teorico (JA, IT). Preparazione e scrittura dell’articolo (JA, IT). In generale, entrambi gli autori hanno contribuito allo sviluppo di questo lavoro.,
Finanziamento
Il primo autore ha comunicato di aver ricevuto il seguente sostegno finanziario per la ricerca, la paternità e / o la pubblicazione di questo articolo: ha ricevuto un sostegno finanziario dalla Commissione nazionale cilena per la ricerca scientifica e tecnologica (CONICYT) “Becas Chile” Doctoral Fellowship program (Grant no: 72140548).
Dichiarazione sul conflitto di interessi
Gli autori dichiarano che la ricerca è stata condotta in assenza di relazioni commerciali o finanziarie che potrebbero essere interpretate come un potenziale conflitto di interessi.
Cronbach, L. (1951)., Coefficiente alfa e struttura interna dei test. Psychometrika 16, 297-334. doi: 10.1007/BF02310555
CrossRef Full Text / Google Scholar
McDonald, R. (1999). Teoria dei test: un trattamento unificato. I nostri servizi sono a vostra disposizione.
Google Scholar
R Team di sviluppo principale (2013). R: Un linguaggio e un ambiente per il calcolo statistico. Vienna: R Fondazione per l’informatica statistica.
Raykov, T. (1997)., Scale reliability, cronbach”s coefficient alpha, and violations of essential tau- equivalence with fixed congeneric components. Multivariate Behav. Res. 32, 329–353. doi: 10.1207/s15327906mbr3204_2
PubMed Abstract | CrossRef Full Text | Google Scholar
Raykov, T. (2001). Bias of coefficient alpha for fixed congeneric measures with correlated errors. Appl. Psychol. Meas. 25, 69–76. doi: 10.1177/01466216010251005
CrossRef Full Text | Google Scholar
Revelle, W. (2015b). Package “psych.,”Disponibile online all’indirizzo: http://org/r/psych-manual.pdf
Shapiro, A., e ten Berge, JMF (2000). Il bias asintotico dell’analisi del fattore di traccia minimo, con applicazioni al massimo inferiore legato all’affidabilità. Psychometrika 65, 413-425. doi: 10.1007 | BF02296154
CrossRef Full Text/Google Scholar
ten Berge, JMF, and Sočan, G. (2004). Il massimo inferiore legato all’affidabilità di un test e all’ipotesi di unidimensionalità. Psychometrika 69, 613-625. doi: 10.,1007 | BF02289858
CrossRef Full Text/Google Scholar
Woodhouse, B., e Jackson, P. H. (1977). Limiti inferiori per l’affidabilità del punteggio totale su un test composto da elementi non omogenei: II: una procedura di ricerca per individuare il massimo limite inferiore. Psychometrika 42, 579-591. doi: 10.1007 | BF02295980
CrossRef Full Text/Google Scholar
Appendice I
Sintassi R per stimare i coefficienti di affidabilità dalle matrici di correlazione di Pearson., La correlazione dei valori al di fuori della diagonale sono calcolati moltiplicando il fattore di carico degli elementi: (1) tau-modello equivalente sono tutti uguali, per 0.3114 (λiλj = 0.558 × 0.558 = 0.3114) e (2) congenerica modello possono variare in funzione del fattore di carico (ad esempio, l’elemento di matrice di a1, 2 = λ1λ2 = 0.3 × 0.4 = 0.12). In entrambi gli esempi la vera affidabilità è 0.731.
> omega(Cr,1) alpha alpha # standardized Cronbach”s α
0.731
> omega(Cr,1) omega omega.tot # coefficiente ω totale
0.,731
> glb.fa(Cr)$glb # GLB factorial procedure
0.731
> glb.algebraic(Cr)$glb # GLB algebraic procedure
0.731
> omega(Cr,1)$alpha # standardized Cronbach”s α
0.717
> omega(Cr,1)$omega.tot # coefficient ω total
0.731
> glb.fa(Cr)$glb # GLB factorial procedure
0.754
> glb.algebraic(Cr)$glb # GLB algebraic procedure
0.731