Un modello di regressione per i dati di sopravvivenza
In precedenza ho scritto su come calcolare la curva di Kaplan–Meier per i dati di sopravvivenza. Come stimatore non parametrico, fa un buon lavoro nel dare una rapida occhiata alla curva di sopravvivenza per un set di dati. Tuttavia, ciò che non ti consente di fare è modellare l’impatto delle covariate sulla sopravvivenza. In questo articolo, ci concentreremo sul modello di rischi proporzionali Cox, uno dei modelli più utilizzati per i dati di sopravvivenza.
Andremo in profondità su come calcolare le stime., Questo è prezioso perché vedremo che le stime dipendono solo dall’ordinamento dei guasti e non dai loro tempi effettivi. Discuteremo anche brevemente alcune questioni complicate sull’inferenza causale che sono speciali per l’analisi della sopravvivenza.
In genere pensiamo ai dati di sopravvivenza in termini di curve di sopravvivenza come quella qui sotto.,
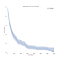
Sull’asse x, abbiamo il tempo in giorni. Sull’asse y, abbiamo (uno stimatore per) la percentuale (tecnicamente, proporzione) di soggetti nella popolazione che “sopravvivono” a quel tempo. Sopravvivere può essere figurativo o letterale., Potrebbe essere se le persone vivono fino a una certa età, se una macchina lo rende una certa quantità di tempo senza rompersi, o potrebbe essere se qualcuno rimane disoccupato una certa quantità di tempo dopo aver perso il lavoro.
Fondamentalmente, la complicazione nell’analisi della sopravvivenza è che alcuni soggetti non hanno la loro “morte” osservata. Potrebbero essere ancora vivi, una macchina potrebbe ancora funzionare o qualcuno potrebbe essere ancora disoccupato al momento della raccolta dei dati., Tali osservazioni sono chiamate “censurate a destra” e trattare con la censura significa che l’analisi della sopravvivenza richiede diversi strumenti statistici.
Denotiamo la funzione survivor come S, una funzione del tempo. Il suo output è la percentuale di soggetti sopravvissuti al tempo t. (Di nuovo, è tecnicamente una proporzione tra 0 e 1, ma userò le due parole in modo intercambiabile). Per semplicità faremo il presupposto tecnico che se aspettiamo abbastanza a lungo tutti i soggetti ” moriranno.”
Indicizzeremo i soggetti con un pedice come i o j., Il fallimento volte di tutta la popolazione, sarà indicato con un simile indice sulla variabile tempo t.

Un’altra sottigliezza da considerare è se stiamo trattando tempo discreto (di settimana in settimana, per esempio) o in continuo. Filosoficamente parlando, misuriamo sempre e solo il tempo in incrementi discreti (al secondo più vicino, diciamo)., Comunemente i nostri dati ci diranno solo se qualcuno è morto in un dato anno o se una macchina ha fallito in un dato giorno. Andrò avanti e indietro tra i casi discreti e continui nell’interesse di mantenere l’esposizione il più chiara possibile.
Quando stiamo cercando di modellare gli effetti delle covariate (ad esempio età, sesso, razza, produttore della macchina) saremo in genere interessati a comprendere l’effetto della covariata sul tasso di pericolo. Il tasso di pericolo è la probabilità istantanea di fallimento/morte/transizione di stato in un dato momento t, a condizione che sia già sopravvissuto così a lungo., Lo denoteremo λ (t). Il trattamento con tempo discreto:
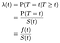
Dove f è il generale di densità di probabilità di fallire al tempo t. Siamo in grado di unificare il discreto e il caso continuo, consentendo delta funzioni di densità di probabilità “funzione”. Quindi il risultato λ = f / S è lo stesso per il caso continuo.
Correggiamo un esempio., Consideriamo il contesto di uno studio clinico in cui un farmaco provoca inizialmente una malattia in remissione. Diremo che il farmaco “fallisce” per un soggetto quando la malattia inizia a progredire per un soggetto. Infine, supponiamo che gli stati di malattia dei soggetti siano misurati ogni settimana. Quindi se λ(3) = 0.1, ciò significa che c’è una probabilità del 10% che, per un dato soggetto, se sono ancora in remissione prima della settimana 3, la loro malattia inizierà a progredire alla settimana 3. L’altro 90% rimarrà in remissione.,
Successivamente, la funzione di densità di probabilità complessiva f è solo la derivata di S rispetto al tempo. (Ancora una volta, se il tempo è discreto, f è solo la somma di alcune funzioni delta).,341fa8b2″>
Questo significa che se conosciamo la funzione di rischio, siamo in grado di risolvere questa equazione differenziale per S:
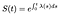
Se il tempo è discreto, l’integrale di una somma di delta funzioni si trasforma in una somma di pericoli in ogni tempo discreto.,
Ok, questo riassume la notazione e i concetti di base di cui avremo bisogno. Passiamo alla discussione dei modelli.
Modelli non-, Semi-e completamente parametrici
Come ho detto prima, siamo tipicamente interessati a modellare il tasso di pericolo λ.
In un modello non parametrico, non facciamo ipotesi sulla forma funzionale di λ. La curva di Kaplan–Meier è lo stimatore di massima verosimiglianza in questo caso. Il rovescio della medaglia è che questo rende difficile modellare qualsiasi effetto delle covariate. È un po ‘ come usare un grafico a dispersione per capire l’effetto di una covariata., Non necessariamente utile come un modello completamente parametrico come una regressione lineare.
In un modello completamente parametrico, facciamo un’ipotesi per la forma funzionale precisa di λ. Una discussione dei modelli completamente parametrici è un articolo completo a sé stante, ma vale la pena una breve discussione. La tabella seguente mostra tre dei modelli completamente parametrici più comuni. Ciascuno è generalizzato dal successivo, passando da 1 a 2 a 3 parametri. Il modulo funzionale per la funzione di pericolo è mostrato nella colonna centrale. Il logaritmo della funzione di pericolo è anche mostrato nell’ultima colonna., Tutti i parametri (ɣ, α, μ) sono considerati positivi tranne che μ potrebbe essere 0 nella distribuzione di Weibull generalizzata (riproducendo la distribuzione di Weibull).

Guardando il logaritmo ci mostra che il modello esponenziale assume che la funzione di rischio è costante. Il modello di Weibull presuppone che sia crescente se α>1, costante se α=1 e decrescente se α<1., Il modello di Weibull generalizzato inizia allo stesso modo del modello di Weibull (all’inizio ln S = 0). Dopo di che, un termine in più μ calci in.
Il problema con questi modelli è che fanno forti ipotesi sui dati. In alcuni contesti, ci possono essere ragioni per credere che questi modelli siano una buona misura. Ma con queste e molte altre opzioni disponibili, c’è un forte rischio di trarre conclusioni errate a causa di errori di specificazione del modello.
Questo è il motivo per cui il Cox Pericoli proporzionali, un modello semi-parametrico è così popolare., Non vengono fatte ipotesi funzionali sulla forma della Funzione di pericolo; invece, le ipotesi di forma funzionale sono fatte sugli effetti delle covariate da sole.,
Il rischio Proporzionale di Cox del Modello
Il rischio Proporzionale di Cox del Modello è di solito dato in termini di tempo t, covariata vettore x, e coefficiente di vettore β
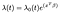
dove il λₒ è una funzione arbitraria di tempo, la previsione di pericolo. Il prodotto punto di X e β è preso nell’esponente proprio come nella regressione lineare standard., Indipendentemente dai valori covariati, tutti i soggetti condividono lo stesso rischio basale λₒ. Successivamente, gli aggiustamenti sono fatti in base alle covariate.
Interpretazione dei Risultati
Supponiamo, per i minuti che abbiamo montare un rischio Proporzionale di Cox del modello per i nostri dati, che consisteva
- Una colonna specifica il tempo per ogni soggetto
- Una colonna specifica se il soggetto è stato “osservato” (fallito, o, nel nostro esempio preferito, per avere il loro progresso della malattia). Un valore di 1 significa che il soggetto ha avuto il loro progresso della malattia., Un valore di 0 significa che, all’ultimo momento di osservazione, la malattia non aveva progredito. L’osservazione è stata censurata.
- Colonne per le nostre covariate X.
Dopo l’adattamento, otterremo i valori per β. Ad esempio, supponiamo per semplicità che esista una singola covariata. Un valore di β = 0,1 significa che un aumento della covariata di una quantità di 1 porta a circa il 10% di probabilità di progressione della malattia in un dato momento., Il valore esatto è in realtà

Per piccoli valori di β, il valore di β in sé è una buona approssimazione della esatta aumento del rischio. Per valori più grandi di β, è necessario calcolare l’importo esatto.
Un altro modo per esprimere β=0.1 è che, all’aumentare di x, il pericolo aumenta ad una velocità del 10% per aumento di x di 1. Il più grande 10.,il 52% deriva dal compounding (continuo), proprio come con l’interesse composto.
Inoltre, β = 0 significa nessun effetto e β negativo significa che c’è meno rischio all’aumentare della covariata. Si noti che, a differenza delle regressioni standard, non esiste un termine di intercettazione. Invece l’intercetta viene assorbita nel rischio di base λₒ, che può anche essere stimato (vedi sotto).
Infine, supponendo di aver stimato la funzione di pericolo di base, possiamo costruire la funzione survivor.,
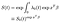
La funzione di base è elevato alla potenza di exp(xʹß) fattore provenienti dalle covariate. Occorre prestare particolare attenzione nell’interpretare la funzione survivor di base, che svolge approssimativamente il ruolo del termine di intercettazione in una regressione lineare regolare. Se le covariate sono state centrate (media 0), rappresenta la funzione survivor per il soggetto “medio”.,
Stima del modello dei rischi proporzionali di Cox
Negli anni ‘ 70, David Cox, un matematico britannico, propose un modo per stimare β senza dover stimare il rischio di base λₒ. Anche in questo caso, il rischio di base può essere stimato in seguito. Come accennato in precedenza, vedremo che è l’ordinamento dei fallimenti osservati che conta, non i tempi stessi.
Prima di saltare nella stima, vale la pena discutere dei legami. Poiché in genere osserviamo solo i dati con incrementi discreti, è possibile che si verifichino due errori contemporaneamente., Ad esempio, due macchine potrebbero fallire nella stessa settimana e la registrazione viene effettuata solo su base settimanale. Questi legami rendono l’analisi della situazione piuttosto complicata senza aggiungere molte intuizioni. Di conseguenza, ricaverò le stime in caso di assenza di legami.
Ricordiamo che i nostri dati sono costituiti da osservazioni di alcuni errori numerici a tempo discreto. Sia R (t) denotare la popolazione “a rischio” al momento t. Se un soggetto nel nostro studio ha fallito (malattia progredita, per esempio) prima del tempo t, non sono “a rischio.,”Inoltre, se un soggetto nel nostro studio ha avuto la loro osservazione censurata in un momento prima del tempo t, anche loro non sono” a rischio.”
Nel solito modo, vogliamo costruire una funzione di verosimiglianza (qual è la probabilità che avremmo osservato i dati che abbiamo fatto, date le covariate e i coefficienti) e quindi ottimizzarlo per ottenere uno stimatore di massima verosimiglianza.
Per ogni tempo discreto in cui abbiamo osservato un fallimento del soggetto j, la probabilità che ciò si verifichi, dato che si è verificato un errore, è inferiore. La somma è presa in consegna tutti i soggetti a rischio al momento j.,

si Noti che la linea di base di pericolo λₒ ha abbandonato! Molto comodo. Per questo motivo, la probabilità che costruiamo è solo una probabilità parziale. Si noti inoltre che i tempi non appaiono affatto., Il termine per soggetto j dipende solo da quali soggetti sono ancora vivi al tempo j, che a sua volta dipende solo dall’ordine in cui i soggetti sono censurati o osservati a fallire.
La probabilità parziale è ovviamente solo il prodotto di questi termini, uno per ogni errore che osserviamo (nessun termine per osservazioni censurate).,
Il log parziale probabilità è quindi
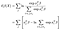
La vestibilità è normale metodi numerici, per esempio il pacchetto python statsmodels e la matrice di varianza-covarianza per le stime è dato da (inversa della Matrice di Informazione di Fisher. Niente di eccitante qui.,
Stima della funzione Survivor Baseline
Ora che abbiamo stimato i coefficienti, possiamo stimare la funzione survivor. Questo finisce per essere molto simile alla stima di una curva Kaplan-Meier.
Postuliamo termini α indicizzati da i. Al momento i, la curva di sopravvivenza al basale dovrebbe diminuire di una frazione α che rappresenta la proporzione di soggetti a rischio che falliscono al momento i., In altre parole,
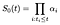
Per calcolare lo stimatore di massima verosimiglianza per α, consideriamo la probabilità contributo da parte di soggetti che non riesce a periodo io e separatamente il contributo di coloro che sono censurati al tempo i.
Per un soggetto che non riesce al tempo i, la probabilità è data dalla probabilità che essi sono vivi al momento ho meno la probabilità che vivo la prossima volta che i+1. (Assumiamo temporaneamente che i tempi siano ordinati).,
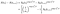
Se invece vengono censurate al tempo i, il contributo è solo la probabilità che essi sono vivi al momento dopo che io, cioè che non è morto di sicurezza., Questo è solo
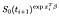
C’è un ulteriore termine di soggetti che sono stati osservati (cioè osservato esito negativo invece censurate)., La log-verosimiglianza diventa
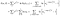
sono stato un po ‘ sciatta di tenere traccia di endpoint (io contro i+1), ma tutto il lavoro fuori.
Ci sono solo termini α per i soggetti che abbiamo osservato fallire., Differenziando rispetto a α-j e assumendo nessun legame, otteniamo un contributo dalla somma a sinistra solo per i soggetti vivi al tempo j, e un singolo contributo dal termine a destra.,qual è 0 significa che siamo in grado di ottenere la stima di massima verosimiglianza per α utilizzando le nostre stime per β come la soluzione per le diverse equazioni, una per ogni soggetto è stato osservato un errore:
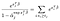
Estensioni e Avvertenze
non C’è molto di più da dire su di Rischi Proporzionali di Cox modelli, ma cerco di mantenere le cose in breve, e per citare solo un paio di cose.,
Ad esempio, si può prendere in considerazione regressori variabili nel tempo, e questo è possibile.
L’altra cosa cruciale da tenere a mente è omesso il bias variabile. Nella regressione lineare standard, le variabili omesse non correlate ai regressori non sono un grosso problema. Questo non è vero nell’analisi di sopravvivenza. Supponiamo di avere due sottopopolazioni di dimensioni uguali e campionate nei nostri dati ciascuna con un tasso di pericolo costante, una è 0.1 e l’altra è 0.5. Inizialmente, vedremo un alto tasso di pericolo (la media, solo 0,3)., Col passare del tempo, la popolazione con un alto tasso di pericolo lascerà la popolazione e osserveremo un tasso di pericolo che diminuisce verso 0.1. Se omettiamo la variabile che rappresenta queste due popolazioni, il nostro tasso di rischio di base sarà tutto incasinato.