
Pitagora
Oltre 2000 anni fa ci fu una scoperta sorprendente sui triangoli:
Quando un triangolo ha un angolo retto (90°) …
… e i quadrati sono fatti su ciascuno deitre lati, …
… quindi la piazza più grande ha la stessa identica area degli altri due quadrati messi insieme!,
si chiama “Pitagora” Teorema” e può essere scritto in una sola equazione:
a2 + b2 = c2
Nota:
- c è il lato più lungo del triangolo
- a e b sono gli altri due lati
Definizione
Il lato più lungo del triangolo è chiamato il “ipotenusa”, così la definizione formale è:
In un ad angolo retto del triangolo:
il quadrato dell’ipotenusa è uguale a
la somma dei quadrati degli altri due lati.,
Certo … ?
Vediamo se funziona davvero usando un esempio.

Perché è utile?
Se conosciamo le lunghezze di due lati di un triangolo rettangolo, possiamo trovare la lunghezza del terzo lato. (Ma ricorda che funziona solo su triangoli ad angolo retto!)
Come lo uso?,
Scrivi come un’equazione:
 |
a2 + b2 = c2 |
Quindi usiamo algebra di trovare qualsiasi valore mancante, come in questi esempi:
Si può anche leggere su Quadrati e Radici Quadrate per scoprire perché √169 = 13
funziona in un altro modo, troppo: quando i tre lati di un triangolo rendere a2 + b2 = c2, allora il triangolo è ad angolo retto.,
E puoi dimostrare il teorema da solo !
Prendi carta penna e forbici, quindi usa la seguente animazione come guida:
- Disegna un triangolo rettangolo sulla carta, lasciando molto spazio.,
- Disegnare un quadrato lungo l’ipotenusa (il lato più lungo)
- Disegnare lo stesso quadrato di dimensioni sull’altro lato dell’ipotenusa
- Disegnare linee come mostrato sull’animazione, come questo:

- ritaglia le forme
- disporli in modo che è possibile dimostrare che il quadrato grande ha la stessa area come il due piazze, sugli altri lati
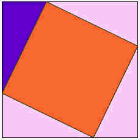
un Altro, Incredibilmente Semplice, Prova
Qui si trova una delle più antiche prove che la piazza sul lato lungo ha la stessa area, come le altre piazze.,
Guarda l’animazione e fai attenzione quando i triangoli iniziano a scivolare.
Si consiglia di guardare l’animazione un paio di volte per capire cosa sta succedendo.
Il triangolo viola è quello importante.
 |
diventa | 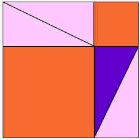 |

