“I, in ogni caso, sono convinto che non lancia dadi.,”
~ Albert Einstein
- Variabili Casuali
- Variabili Casuali Discrete
- Variabili Casuali Continue
- Misto di Variabili Casuali
- Funzioni di Distribuzione Cumulativa (CDF)
- Funzione di Densità di Probabilità (PDF)
- Interactive CDF/PDF Esempio
Variabili Casuali:

Dire che siete stati di prendere una moneta dalla tasca e la getta in aria. Mentre gira attraverso lo spazio, cosa potresti dire del suo futuro?
Atterrerà heads up? Croce?, Più di questo, per quanto tempo rimarrà in aria? Quante volte rimbalzerà? Quanto lontano da dove colpisce per la prima volta il suolo si fermerà finalmente? Del resto, colpirà mai il suolo? Mai venuto a riposare?
Per alcune di queste domande, possiamo e sistemiamo le risposte molto prima delle osservazioni; siamo abbastanza sicuri che la gravità reggerà e la moneta atterrerà. Ma per gli altri non abbiamo altra scelta che giudicare e parlare in termini più vaghi, se vogliamo dire qualcosa di utile sul futuro.,
Come scienziati, è, ovviamente, il nostro lavoro dire qualcosa di utile (o per lo meno, autorevole…), mentre le monete metaforiche di importanti sistemi fisici sono ancora nell’aria. Testa o croce può anche essere una questione di vita o di morte. Le nostre monete possono essere, ad esempio, varie possibili portate di refrigerante o masse di uranio in una centrale nucleare. Ci preoccupiamo molto di sapere quali sono le nostre possibilità che otterremo turbine ronzio invece di un tracollo.,
Per un rigoroso determinista, tutte queste scommesse sono state risolte molto prima che qualsiasi moneta, metaforica o meno, fosse mai coniata; semplicemente non lo sappiamo ancora. Se sapessimo solo le forze applicate al lancio di una moneta, la sua esatta distribuzione della massa, i vari movimenti minuti di aria nella stanza… Se sapessimo tutto questo, allora sapremmo che quel particolare lancio di monete aveva una probabilità del 100% di atterrare nel modo in cui atterrerà, e zero possibilità di qualsiasi altro risultato.
Ma a noi, naturalmente, manca spesso anche una frazione menzionabile di tale conoscenza del mondo., Inoltre, sembra su scale estremamente piccole che i deterministi rigorosi siano assolutamente sbagliati; non c’è modo di prevedere quando, ad esempio, un atomo di uranio si dividerà, e se un tale evento influenza il mondo più grande allora quell’evento macro è veramente imprevedibile. Alcuni risultati sono veramente nell’aria, instabili fino a quando non fanno parte del passato.
Per far fronte a questa realtà e per essere in grado di descrivere gli stati futuri di un sistema in qualche modo utile, usiamo variabili casuali., Una variabile casuale è semplicemente una funzione che mette in relazione ogni possibile risultato fisico di un sistema con un numero reale univoco. Come tale ci sono tre tipi di variabili casuali: discrete, continue e miste. Nelle sezioni seguenti queste categorie saranno brevemente discusse e verranno forniti esempi.
Variabili casuali discrete:
Considera di nuovo il nostro lancio della moneta. Potremmo avere testa o croce come possibili risultati. Se definiamo una variabile, x, come il numero di teste in un singolo lancio, allora x potrebbe essere 1 o 0, nient’altro., Tale funzione, x, sarebbe un esempio di una variabile casuale discreta. Tali variabili casuali possono assumere solo valori discreti. Altri esempi potrebbero essere i possibili risultati di un test di gravidanza o il numero di studenti in una classe.
Variabili casuali continue:
Torna al lancio della moneta, e se volessimo descrivere la distanza tra dove la nostra moneta si è fermata e dove ha colpito per la prima volta il terreno. Quella distanza, x, sarebbe una variabile casuale continua perché potrebbe assumere un numero infinito di valori all’interno dell’intervallo continuo di numeri reali., La moneta potrebbe viaggiare 1 cm, o 1,1 cm, o 1,11 cm, o su e su. Altri esempi di variabili casuali continue sarebbero la massa delle stelle nella nostra galassia, il pH delle acque oceaniche o il tempo di permanenza di qualche analita in un gascromatografo.
Variabili casuali miste:
Le variabili casuali miste hanno componenti sia discreti che continui. Tali variabili casuali si incontrano raramente. Per un possibile esempio, anche se, si può misurare il peso di un campione e decidere che qualsiasi peso misurato come valore negativo sarà dato un valore di 0., In questo modo la variabile casuale ha un componente discreto a x = 0 e un componente continuo dove x > 0.
Cumulative Distribution Functions (CDF):
La domanda, ovviamente, sorge su come meglio descrivere matematicamente (e visualizzare visivamente) le variabili casuali. Per tali attività utilizziamo le funzioni di densità di probabilità (PDF) e le funzioni di densità cumulativa (CDF). Poiché i CDF sono più semplici da comprendere per variabili casuali discrete e continue rispetto ai PDF, spiegheremo prima i CDF.
Considera di lanciare un dado a 6 lati., Avremmo una probabilità 1 su 6 di ottenere uno qualsiasi dei possibili valori della variabile casuale (1, 2, 3, 4, 5, o 6). Se tracciamo quei possibili valori sull’asse x e tracciamo la probabilità di misurare ogni valore specifico, x o qualsiasi valore inferiore a x sull’asse y, avremo il CDF della variabile casuale.
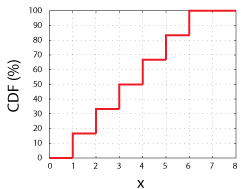
CDF per una fiera dadi 6 lati. Si noti che ogni passo è un’altezza del 16,67%, o 1 su 6.
Questa funzione, CDF(x), ci dice semplicemente le probabilità di misurare qualsiasi valore fino a x incluso., In quanto tale, tutti i CDF devono avere tutte queste caratteristiche:
- Un CDF deve essere uguale a 0 quando x = – ∞ e avvicinarsi a 1 (o 100%) quando x si avvicina a +∞. In poche parole, tra tutti i possibili risultati, ci deve essere un risultato; la possibilità di lanciare un dado a sei facce e ottenere un valore tra -∞ e ∞ è del 100%.
- La pendenza di un CDF deve essere sempre uguale o maggiore di zero. Ad esempio, considera la possibilità di lanciare un dado a 6 lati (giusto o meno) e ottenere un valore compreso tra 0 e 4., Questa possibilità non può essere più della possibilità di ottenere un valore compreso tra 0 e 5, perché le probabilità di un atterraggio 1, 2 o 3 a faccia in su sono, ovviamente, sempre una frazione delle probabilità di ottenere un 1, 2, 3 o 4.
Per un esempio di variabile casuale continua, l’applet seguente mostra il CDF normalmente distribuito.,div>
| -5 | 5 |
| x | |
This important distribution is discussed elsewhere., Basta notare che le caratteristiche di un CDF descritte sopra e spiegate per una variabile casuale discreta valgono anche per variabili casuali continue.
Per esempi più intuitivi delle proprietà di CDFs, vedere l’esempio interattivo di seguito. Inoltre, grafici interattivi di molti altri CDF importanti per il campo delle statistiche e utilizzati su questo sito possono essere trovati qui.
Funzioni di densità di probabilità (PDF):
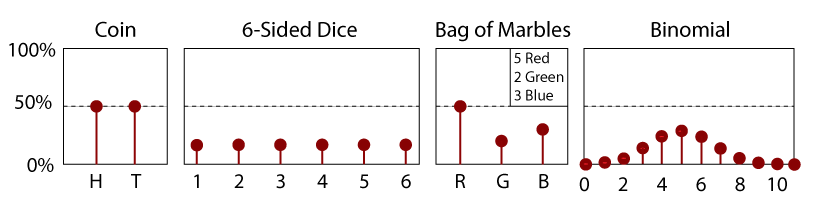
PDF per una fiera dadi 6 lati.
Un PDF è semplicemente la derivata di un CDF., Quindi un PDF è anche una funzione di una variabile casuale, x, e la sua grandezza sarà un’indicazione della probabilità relativa di misurare un particolare valore. Poiché è la pendenza di un CDF, un PDF deve essere sempre positivo; non ci sono quote negative per qualsiasi evento. Inoltre e per definizione, l’area sotto la curva di un PDF(x) tra -∞ e x è uguale al suo CDF(x). Come tale, l’area tra due valori x1 e x2 dà la probabilità di misurare un valore all’interno di tale intervallo.
L’applet seguente mostra un esempio di PDF per una variabile casuale normalmente distribuita, x.,
Normal PDF
|
x:
| mean:
| stdev:
| f(x):
|
|
Notice, when the mean and standard deviations are equal, how the PDF correlates with the normal CDF in the section above., Considera anche la differenza tra un PDF continuo e discreto. Mentre un PDF discreto (come quello mostrato sopra per dice) ti darà le probabilità di ottenere un risultato particolare, le probabilità con PDF continui sono questioni di intervallo, non di punti discreti. Ad esempio, c’è chiaramente un 1 su 6 (16,6%) possibilità di tirare un 3 su un dado, come si può vedere nel suo PDF. Ma quali sono le dispari di misurare esattamente zero con una variabile casuale con un PDF normale e una media di zero, come mostrato sopra? Anche se è il valore in cui il PDF è il più grande, la possibilità di misurare esattamente 0.00000..,. è, forse contro intuitivamente, zero. Le probabilità di misurare qualsiasi particolare numero casuale a precisione infinita sono, infatti, zero. Con un PDF continuo puoi invece chiedere quali sono le probabilità che misurerai tra due valori per ottenere una probabilità maggiore di zero. Per trovare questa probabilità usiamo semplicemente il CDF della nostra variabile casuale., Poiché il CDF ci dice la dispari di misurare un valore o qualcosa di inferiore a quel valore, per trovare la probabilità di misurare tra due valori, x1 e x2 (dove x1 > x2), dobbiamo semplicemente prendere il valore del CDF a x1 e sottrarre da esso il valore del CDF a x2. Ad esempio, usando il normale CDF nell’applet sopra (con μ=0 e σ=1), se volessimo conoscere le probabilità di misurare tra 0.01 e 0.02 troviamo CDF(x=0.1)=53.9828% e CDF(x=0.2)=57.9260%. Quindi la differenza, CDF (0.2) – CDF(0.1), ci dà le probabilità di circa il 3.9% di misurare una x tra 0.1 e 0.2., Per esempi visivi più intuitivi delle proprietà dei PDF, vedere l’esempio interattivo di seguito. Inoltre, trame interattive di molti importanti PDF utilizzati su questo sito possono essere visti qui. |
|||||||||||||||||