ANOVAテスト：定義、タイプ、例

Posted on
シェアオン

統計定義>ANOVA
内容：

  1. ANOVAテスト
  2. 一方向ANOVA
  3. 双方向分散分析
  4. マノバとは何ですか？
  5. 階乗分散分析とは何ですか？
  6. ANOVAを実行する方法
  7. ANOVA vs.Tテスト
  8. 反復測定ANOVA
  9. 真球度

ANOVAテスト

ANOVAとは何ですか？, 導入のためのビデオを見る、または以下を読む：

このビデオを見るために統計、マーケティングクッキーを受け入れてください。

まだ問題がありますか？ Chegg.com 家庭教師とあなたにマッチします（あなたの最初のレッスンは無料です！).ANOVA検定は、調査または実験の結果が有意であるかどうかを調べる方法です。 言い換えれば、帰無仮説を棄却する必要があるのか、代替仮説を受け入れる必要があるのかを把握するのに役立ちます。

基本的には、グループ間に違いがあるかどうかを確認するためにグループをテストしています。, 異なるグループをテストする場合の例：

  • 精神科患者のグループは、カウンセリング、投薬、バイオフィードバックの三つの異なる治療法を試しています。 ある治療法が他の治療法よりも優れているかどうかを確認したいです。
  • メーカーは電球を作るために二つの異なるプロセスを持っています。 彼を知りたい場合過程による。
  • 異なる大学の学生は同じ試験を受けます。 ある大学が他の大学よりも優れているかどうかを確認したいです。li>

“一方向”または”双方向”とはどういう意味ですか？,

一方向または双方向は、分散分析テストにおける独立変数（Iv）の数を指します。

  • 一方向は独立変数（2つのレベルを持つ）を持ちます。 例えば：穀物のブランド、
  • 双方向は二つの独立変数を持っています（それは複数のレベルを持つことができます）。 例えば：穀物のブランド、カロリー。 li>

“グループ”または”レベル”とは何ですか？

グループまたはレベルは、同じ独立変数内の異なるグループです。 上記の例では、”穀物のブランド”のためのあなたのレベルは、幸運のお守り、レーズンふすま、コーンフレークかもしれない—三つのレベルの合計。, “カロリー”のためのあなたのレベルは次のとおりであるかもしれない:甘くされて、無糖—二つのレベルの合計。

アルコールサポートグループと個々のカウンセリングを組み合わせたものがアルコール消費量を減らすための最も効果的な治療法であるかどうかを調

  • 投薬のみ、
  • 投薬とカウンセリング、
  • カウンセリングのみです。

    • カウンセリングのみです。
      • カウンセリングのみです。

      従属変数は、一日あたり消費されるアルコール飲料の数になります。,

      グループまたはレベルに階層構造がある場合（各レベルに一意のサブグループがある場合）、分析にネストされたANOVAを使用します。

      “複製”とはどういう意味ですか？

      テストを複数のグループで複製（つまり複製）しているかどうかです。 複製付きの双方向ANOVAでは、二つのグループがあり、そのグループ内の個人は複数のことを行っています（つまり、二つの大学からの学生の二つのグループが二 二つのテストを受けているグループが一つしかない場合は、複製なしで使用します。

      テストの種類。,

      一方向と双方向の二つの主なタイプがあります。 双方向テストは、複製の有無にかかわらず可能です。

      • グループ間の一方向ANOVA：二つのグループをテストして、それらの間に違いがあるかどうかを確認するときに使用されます。
      • レプリケーションなしの双方向ANOVA：一つのグループがあり、同じグループを二重テストしているときに使用されます。 たとえば、あなたは彼らがそれが動作するかどうかを確認するために薬を服用する前と後に個人のセットをテストしています。
      • レプリケーションと双方向ANOVA：二つのグループ、およびそれらのグループのメンバーは、複数のことをやっています。, 例えば、両グループからの検診希望者-治療患者別の病院のう二つの異なる視野に入りつつあります。

      Back to Top

      One way ANOVA

      one way ANOVAは、F分布を使用して二つの独立した（無関係な）グループから二つの平均を比較するために使用されます。 検定の帰無仮説は、二つの平均が等しいということです。 したがって、重要な結果は、二つの手段が等しくないことを意味する。

      一方向ANOVAを使用する場合の例

      状況1：個人のグループがランダムに小さなグループに分割され、異なるタスクを完了しています。, 例えば、減量に対する茶の効果を調査し、三つのグループを形作るかもしれない:緑茶、紅茶、および茶無し。
      シチュエーション2：シチュエーション1と同様ですが、この場合、個人は自分が持っている属性に基づいてグループに分割されます。 たとえば、体重に応じて人の脚の強さを勉強しているかもしれません。 参加者を体重カテゴリ（肥満、太りすぎ、正常）に分割し、体重マシンで脚の強さを測定することができます。,

      One way ANOVAの制限

      one way ANOVAは、少なくとも二つのグループが互いに異なっていたことを教えてくれます。 しかし、それはどのグループが異なっていたかを教えて 検定が有意なf統計量を返す場合は、アドホック検定（最下位差検定など）を実行して、どのグループが平均に差があるかを正確に伝える必要があります。
      Back to Top

      双方向分散分析

      双方向分散分析は、一方向分散分析の拡張です。 一つの方法では、従属変数に影響を与える独立変数があります。, 双方向分散分析では、二つの独立したものがあります。 あなたは一つの測定変数（つまり、量的変数）と二つの名目変数を持っている場合は、双方向ANOVAを使用してください。 言い換えれば、実験に定量的な結果があり、二つのカテゴリ説明変数がある場合は、双方向ANOVAが適切です。

      たとえば、就職の面接での不安レベルについて、収入と性別の間に相互作用があるかどうかを調べることができます。 不安レベルは、結果、または測定できる変数です。 性別と所得は二つのカテゴリ変数です。, これらのカテゴリ変数は独立変数でもあり、これは双方向ANOVAで因子と呼ばれます。

      因子は水準に分割することができます。 上記の例では、所得レベルは、低所得、中所得、高所得の三つのレベルに分割することができます。 性別は男性、女性、トランスジェンダーの三つのレベルに分けることができます。 治療群は、因子のすべての可能な組み合わせである。 この例では、3x3=9の治療グループが存在するでしょう。

      主効果と相互作用効果

      双方向ANOVAの結果は、主効果と相互作用効果を計算します。, 主効果は一方向ANOVAに似ており、各因子の効果は別々に考慮されます。 相互作用効果では、すべての要因が同時に考慮されます。 各セルに複数の観測値がある場合、因子間の相互作用効果はより簡単にテストできます。 上記の例では、複数のストレススコアをセルに入力することができます。 複数の観測値をセルに入力する場合、各セルの数値は等しくなければなりません。

      あなたが各セルに一つの観測値を置いている場合、二つの帰無仮説が検定されます。, この例では、その仮説する情報を表示します
      H01:すべての利益団体と同等の平均。
      H02:すべての性別のグループは等しい平均ストレスを持っています。

      細胞における複数の観測については、第三の仮説をテストすることもあります。
      H03：因子は独立しているか、相互作用効果が存在しません。

      検定している仮説ごとにF統計量が計算されます。

      双方向分散分析の仮定

      • 母集団は正規分布に近くなければなりません。
      • サンプルは独立している必要があります。
      • 母集団の分散は等しくなければなりません。,
      • li>

      トップに戻る

      マノバとは何ですか？

      MANOVAは、いくつかの従属変数を持つ単なるANOVAです。 これは、独立変数を操作することによって応答変数（つまり従属変数）が変更されたかどうかを調べることが目的であるという点で、他の多くのテス このテストは、次のような多くの研究の質問に答えるのに役立ちます。

      • 独立変数の変更は従属変数に統計的に有意な影響を与えますか？
      • 従属変数間の相互作用は何ですか？,
      • 独立変数間の相互作用は何ですか？

      MANOVA Example

      教科書の違いが数学と科学の学生のスコアに影響を与えるかどうかを調べたいとします。 数学と科学の改善は、二つの従属変数があることを意味するので、MANOVAが適切です。

      ANOVAは単一の（単変量）f値を与え、MANOVAは多変量F値を与えます。 MANOVAは、グループ差を最大化する新しい人工的な従属変数を作成することによって、複数の従属変数を検定します。, これらの新しい従属変数は、測定された従属変数の線形結合です。


      MANOVA結果の解釈

      多変量F値が検定が統計的に有意であることを示す場合、これは何かが有意であることを意味します。 上記の例では、数学のスコアが改善されたか、科学のスコアが改善されたか（またはその両方）を知ることはできません。, 有意な結果が得られたら、個々のコンポーネント（単変量F検定）を調べて、どの従属変数が統計的に有意な結果に寄与したかを確認する必要があります。

      MANOVAとANOVAのメリットとデメリット

      メリット

      1. MANOVAでは、複数の従属変数をテストできます。
      2. MANOVAはタイプIエラーから保護できます。

      短所

      1. MANOVAはANOVAよりも何倍も複雑であるため、どの独立変数が従属変数に影響を与えているかを確認するのは難しいです。,
      2. 一つの自由度は、それぞれの新しい変数を追加すると失われます。
      3. 従属変数はできるだけ無相関でなければなりません。 それらが相関している場合、自由度の損失は、テストに複数の従属変数を含めることに多くの利点がないことを意味します。

      リファレンス：
      （SFSU）

      トップに戻る

      階乗分散分析とは何ですか？

      階乗分散分析は、複数の独立変数、つまり”因子”を持つ分散分析テストです。 また、複数のレベルの独立変数を参照することもできます。, 例えば、治療群と対照群を用いた実験には、一つの要因（治療）がありますが、二つのレベル（治療と対照）があります。 “双方向”および”三方”という用語は、テストの因子の数またはレベルの数を指します。 四元ANOVA以上は、検定の結果が複雑で解釈が困難なため、ほとんど使用されません。

      • 双方向分散分析は、二つの因子（独立変数）と一つの従属変数を持ちます。 たとえば、勉強に費やされた時間と事前知識は、テストでどれだけうまく行うかに影響を与える要因です。,
      • 三元分散分析は、三つの因子（独立変数）と一つの従属変数を持ちます。 たとえば、勉強に費やされた時間、予備知識、睡眠時間は、テストでどれだけうまくいくかに影響する要因です

      階乗分散分析は、テストを行う効率的 ある独立変数をある従属変数に対してテストする一連の実験を実行する代わりに、すべての独立変数を同時にテストすることができます。

      変動性

      一方向ANOVAでは、変動性はグループ間の違いとグループ内の違いによるものです。, 階乗分散分析では、各水準と因子は互いに対になっています（”交差”）。 これにより、水準と因子の間でどのような相互作用が起こっているかを確認できます。 相互作用がある場合、ある因子の違いは別の因子の違いに依存します。

      最終試験で男性/女性のパフォーマンスをテストするために双方向ANOVAを実行していたとしましょう。 被験者は4時間、6時間、または8時間の睡眠を持っていた。,

      • IV1:セックス(男性/女性)
      • IV2:睡眠(4/6/8)
      • DV:最終試験スコア

      双方向階乗分散分析は、次の質問に答えるのに役立ちます。

      1. セックスは主な効果ですか？

        1. セックスは主な効果ですか？

          1. セックスは主な効果ですか？

            1. セックスは主な効果ですか？ 言い換えれば、男性と女性は試験のパフォーマンスに大きく異なりますか？li>
            2. 睡眠は主な効果ですか？ 言い換えれば、睡眠の4,6、または8時間を持っていた人々は、彼らのパフォーマンスが大幅に異なりますか？
            3. 要因間に重要な相互作用はありますか？ 言い換えれば、睡眠時間と性別は試験のパフォーマンスに関してどのように相互作用しますか？,
            4. 睡眠のレベルによって性別や試験のパフォーマンスに違いはありますか？

            階乗ANOVAの仮定

            • 正規性：従属変数は正規分布しています。
            • 独立性：観測とグループは互いに独立しています。
            • 分散の等価性：母分散は因子/レベル間で等しいです。

            ANOVAを実行する方法

            これらのテストは手作業で非常に時間がかかります。 ほぼすべての場合、ソフトウェアを使用する必要があります。, たとえば、Excelではいくつかのオプションが使用できます。

            • Excelでは複製付きおよび複製無しの双方向ANOVAを使用できます。
            • Excel2013の一方向ANOVA。li>

            Excelでテストを実行します。

            統計パッケージのANOVAテストは、パラメトリックデータに対して実行されます。 ランク付けまたは順序付けされたデータがある場合は、ノンパラメトリックANOVAを実行します（通常、”ノンパラメトリックテスト”のようなソフトウェアの別の見出しの下にあります）。,

            Steps

            このテストを手作業で行うことはほとんどありませんが、必要な場合は、次の手順を実行します。

            1. 各グループの平均を見つけます。li>
            2. 全体の平均（グループの平均を組み合わせたもの）を見つけます。
            3. グループ内のバリエーションを見つける;グループ平均からの各メンバーのスコアの合計偏差。
            4. グループ間の変動を見つける：各グループ平均の全体平均からの偏差。
            5. f統計を見つける：グループ変動間のグループ変動内の比。

            ANOVA vs., T検定

            学生のt検定は、グループ間に有意な変動があるかどうかを教えてくれます。 T検定は平均を比較しますが、ANOVAは母集団の間の分散を比較します。
            技術的には、データに対して一連のt検定を実行できます。 ただし、グループの数が増えるにつれて、実行する必要があるペアの比較がたくさん出てしまうことがあります。 ANOVAは、帰無仮説を支持または棄却するのに役立つ単一の数値（f統計量）と一つのp値を与えます。,
            Back to Top

            反復測定分散分析

            反復測定分散分析は、一方向ANOVAとほぼ同じですが、主な違いは一つです：関連するグループをテストし、独立したグループではありません。 同じグループの参加者が何度も何度も測定されているため、これは反復測定と呼ばれています。 たとえば、食事を変更した後、1、3、および6ヶ月で同じグループの患者のコレステロールレベルを研究することができます。 この例では、独立変数は”時間”であり、従属変数は”コレステロール”です。,”独立変数は、通常、被験者内因子と呼ばれます。

            反復測定ANOVAは、単純な多変量計画に似ています。 両方のテストでは、同じ参加者が何度も測定されます。 しかし、反復測定では、同じ特性が異なる条件で測定されます。 例えば、血圧は条件”時間”にわたって測定される。 単純な多変量設計の場合、それは変化する特性である。 たとえば、血圧、心拍数、呼吸数を経時的に測定することができます。,

            反復測定ANOVAを使用する理由

            • 同じ参加者から一定期間にわたってデータを収集すると、個人差（グループ間の差の原因）が減少または排除されます。
            • サンプルサイズがグループ間で分割されていないため、テストはより強力です。
            • 同じ参加者を使用しているので、テストは経済的です。,

            反復測定ANOVAの仮定

            反復測定ANOVAの結果は、次の仮定に違反していない場合にのみ有効です。

            • 独立変数と従属変数が一つある必要があります。
            • 従属変数は、間隔スケールまたは比率スケールの連続変数でなければなりません。
            • 独立変数は、ノミナルスケールまたは序数スケールのいずれかで、カテゴリカルでなければなりません。
            • 理想的には、グループのペア間の依存性のレベルは等しい（”真球度”）。, この仮定に違反した場合、修正が可能です。

            SPSSでの反復測定ANOVA：ステップ

            ステップ1：”分析”をクリックし、”一般線形モデル”の上にカーソルを合わせます。”クリック”反復測定。”

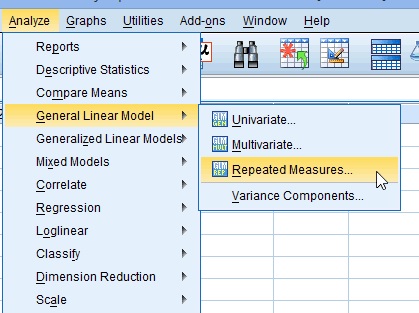
            ステップ2：”factor1″名を独立変数を表すものに置き換えます。 たとえば、”年齢”または”時間”を置くことができます。”

            ステップ3：”レベルの数”を入力します。”これは従属変数が何回測定されたかです。 たとえば、合計4週間毎週測定を行った場合、この数値は4になります。,

            ステップ4：”追加”ボタンをクリックし、従属変数に名前を付けます。ステップ5：”追加”ボタンをクリックします。 反復測定の定義ボックスがポップアップします。 “定義”ボタンをクリックします。

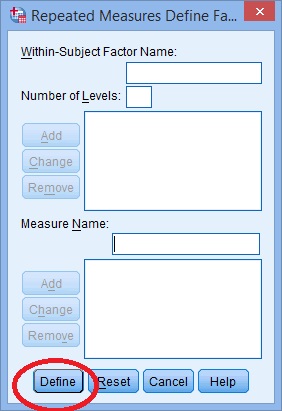
            ステップ6:矢印キーを使用して変数を左から右に移動し、画面が下の画像に似ているようにします。

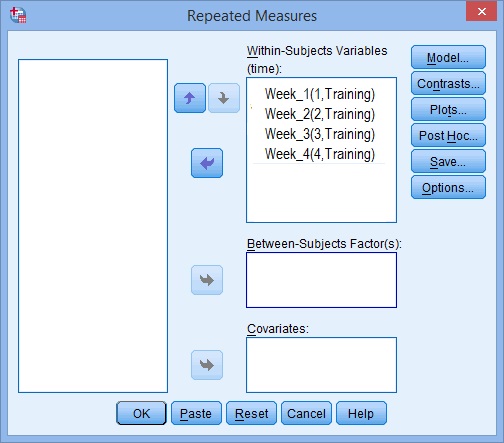
            ステップ7:”プロット”をクリックし、矢印キーを使用して左のボックスから横軸ボックスに因子を転送します。

            ステップ8：”追加”をクリックし、ウィンドウの下部にある”続行”をクリックします。,

            ステップ9：”オプション”をクリックし、左側のボックスから右側のボックスの表示手段に因子を転送します。

            ステップ10:次のチェックボックスをクリックします。

            • 主効果を比較します。
            • 記述統計量。
            • 効果サイズの推定値。

            ステップ11：信頼区間調整の下のドロップダウンメニューから”Bonferroni”を選択します。
            ステップ12：”続行”をクリックし、”OK”をクリックしてテストを実行します。,
            Back to Top

            真球度

            統計において、真球度(θ)は、1940年に最初の汎用電子コンピュータを共同開発したJohn W.Mauchlyによって開発されたMauchlyの真球度検定を指します。

            定義

            繰り返し測定ANOVAの仮定として球形性が使用されます。 仮定は、すべての可能なグループペア間の差の分散が等しいと述べています。 データがこの仮定に違反すると、タイプIエラー（帰無仮説の誤った拒絶）が増加する可能性があります。,

            反復測定ANOVAが仮定に違反することは非常に一般的です。 仮定に違反している場合、タイプI誤り率の増加を避けることができる修正が開発されています。 この補正は、F分布の自由度に適用されます。

            Mauchlyの真球度検定

            Mauchlyの真球度検定は、ほとんどの統計ソフトウェアで実行できます。 Mauchlyのテストは中型のサンプルにとって理想的である。, それは小さいサンプルの球形性を検出しないかもしれ、大きいサンプルで過剰検出するかもしれません。
            検定が小さなp値を返す場合（p≤。05)、これはあなたのデータが仮定に違反していることを示しています。 ANOVAに対するSPSS出力の次の図は、Mauchlyに付随する有意性”sig”があることを示しています。274. これは、このデータセットに対して仮定が違反されていないことを意味します。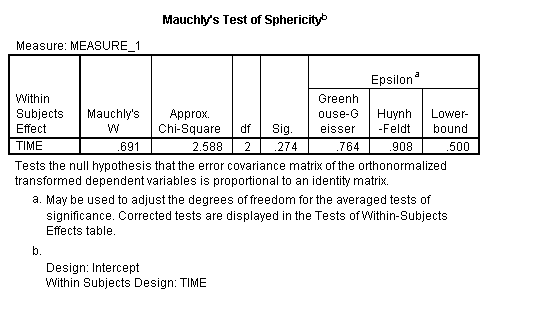


            画像：UVM。,EDU

            上記の結果を”Mauchlyのテストは、球形性の仮定に違反していないことを示しました、φ2（2）=2.588、p=。274.”

            テストで小さなp値が返された場合は、修正を適用する必要があります。

            • Greehouse-Geisser補正。
            • Huynh-Feldt補正。

            ≤0.75の場合（または統計の値がわからない場合）、温室ガイサー補正を使用します。
            とき¶>。75、Huynh-Feldt補正を使用してください。, p>

            トップに戻る

            グランド平均
            分散分析と回帰

            ——————————————————————————

            宿題やテストの質問に助けが必要ですか？ Chegg Studyを使用すると、その分野の専門家からあなたの質問に対するステップバイステップの解決策を得ることができます。 Cheggの家庭教師とのあなたの最初の30分は無料です！

コメントを残す

メールアドレスが公開されることはありません。 * が付いている欄は必須項目です