Pythagoras”Theorem

Pythagoras

2000年以上前に三角形についての驚くべき発見がありました：

三角形が直角（90°）を持つとき。..

。.. そして、正方形は、三つの側面のそれぞれに作られています。..

。.. その後、最大の正方形は、一緒に入れて他の二つの正方形とまったく同じ面積を持っています！,

それは”ピタゴラス”定理”と呼ばれ、一つの短い方程式で書くことができます：

a2+b2=c2

注：p

• cは三角形の最も長い辺です
• aとbは他の二つの辺です

定義

三角形の最も長い辺は”斜辺”と呼ばれるので、正式な定義は次のとおりです。

確かに。.. ?

例を使って実際に動作するかどうかを見てみましょう。

これが便利なのはなぜですか？

直角三角形の二辺の長さを知っていれば、三辺の長さを見つけることができます。 （しかし、それは直角三角形でのみ動作することを覚えています！）

どうやって使うのですか？,

式として書き留めます。

次に、これらの例のように、代数を使用して欠損値を見つけます。

正方形と平方根について読んで、なぜ№169=13

三角形の三辺がa2+b2=c2になると、三角形は直角三角形になります。,

そして、あなたは定理を自分で証明することができます！

紙のペンとはさみを取得し、次のアニメーションをガイドとして使用します。

• たくさんのスペースを残して、紙の上に直角三角形を描きます。,
• 斜辺（最も長い辺）に沿って正方形を描く
• 斜辺の反対側に同じサイズの正方形を描く
• アニメーションに示されているように線を描く：
• 
• 図形を切り取る
• 大きな正方形が他の辺の二つの正方形と同じ面積を持つことを証明できるように配置する

もう一つの、驚くほど単純な、証明

ここでは、長辺の正方形が他の正方形と同じ面積を持つという最も古い証明の一つです。,

アニメーションを見て、三角形が周りにスライドし始めるときに注意を払います。

あなたは何が起こっているかを理解するためにアニメーションを数回見たい場合があります。

紫色の三角形は重要なものです。

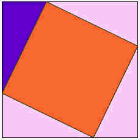になります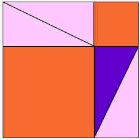