数値の指数は、乗算でその数値を何回使用するかを示します。
82では、”2″は乗算で8倍を使用すると言うので、82=8×8=64
言葉では、82は”8 2乗”または”8乗”、または単に”8乗”と呼ばれることがある。
指数はべき乗またはインデックスとも呼ばれる。,p>いくつかのより多くの例:
例: 53 = 5 × 5 × 5 = 125
- 言葉で言うと、53は”5の三乗”、”5の3乗”、または単に”5立方体”と呼ぶことができます
例: 24 = 2 × 2 × 2 × 2 = 16
- 言葉では、24は”2の四乗”または”2の4乗”または単に”2の4乗”と呼ぶことができます
指数は、多くの乗算を書き込んで使用することを容易にします
例:96は書き込みと読み9 × 9 × 9 × 9 × 9 × 9
指数を使用して、任意の数を何度でも掛けることができます。,
ここで試してみてください:
一般的には
だから一般的には:
| anは、それ自体でaを乗算するように指示します だから、それらのnがあります”s: |
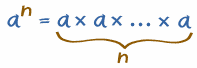 |
別の書き方
入力が簡単なので、^記号(キーボードの6の上)を使用することがあります。
例:2^4は24と同じです
- 2^4 = 2 × 2 × 2 × 2 = 16
負の指数
負?, 乗算の反対は何でしょうか? ディヴィジョン これは1numberで乗算するのと同じです。
例:8-1=18=0.125
このように続けることができます。
例: 5-3 = 15 × 15 × 15 = 0.008
しかし、このようにする方が簡単です:
5-3は次のように計算することもできます。
15 × 5 × 5 = 153 = 1125 = 0.008
ネガティブ? ポジティブをフリップ!,
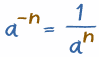 |
最後の例では、負の指数を処理する簡単な方法を示しました。
|
More Examples:
| Negative Exponent | Reciprocal of Positive Exponent |
Answer | ||
|---|---|---|---|---|
| 4-2 | = | 1 / 42 | = | 1/16 = 0.0625 |
| 10-3 | = | 1 / 103 | = | 1/1,000 = 0.001 |
| (-2)-3 | = | 1 / (-2)3 | = | 1/(-8) = -0.,125 |
指数が1または0の場合はどうなりますか?
| 1 | 指数が1の場合、数自体があります(例91=9) | |||||||||
| 0 | 指数が0の場合、1が得られます(例90=1) | |||||||||
| しかし、00はどうですか? それは1または0のいずれかである可能性があるので、人々はそれが”不確定”であると言います。, |
それはすべて理にかなっています
その表を見ると、正、ゼロ、または負の指数は本当に同じ(かなり単純な)パターンの一部
