8.1a historical example
彼の本、The Two New Sciences、Galileo Galilea(1564-1642)の中で、実際の無限または実際の無限小のようなものは存在しないことを示すためのいくつかの議論を与えている。 彼の議論の一つは、次のように再構築することができます。 ガリレオは、自然数の実際の無限大があることを前提とすることを提案しています(自然数は1からの正の整数です)。
{1, 2, 3, 4, 5, 6, 7, ….,}
彼はまた、自然数の二乗の実際の無限大があるという前提として取ることを提案しています。
{1, 4, 9, 16, 25, 36, 49, ….}
さて、ガリレオの理由は、これら二つのグループ(今日、我々はそれらを”セット”と呼ぶだろう)が同じサイズを持っていることに注意してください。 二つのグループの間に一対一の対応があることがわかるので、これを見ることができます。,
| {1, | 2, | 3, | 4, | 5, | 6, | 7, ….,div> | |
| {1, | 4, | 9, | 16, | 25, | 36, | 49,…} |
すべての自然数を一つだけの平方数に関連付けることができ、すべての平方数を一つだけの自然数に関連付けることができれば、これらのセットは同じサイズでなければなりません。,
しかし、ちょっと待って、ガリレオは言います。 明らかに、正方形の数よりも非常に多くの自然数があります。 つまり、すべての平方数は自然数のリストにありますが、自然数の多くは平方数のリストにはありません。 次の数はすべて自然数のリストにありますが、正方形の数のリストにはありません。
{2, 3, 5, 6, 7, 8, 10, ….,}
だから、ガリレオの理由がある場合は、多くの数字のグループの自然数ではないグループの正方形の番号がない場合は、数字のグループの正方形の番号ではない自然数、その自然数よりも大きい正方形の番号です。 そして、自然数のグループが平方数のグループよりも大きい場合、自然数と平方数は同じサイズではありません。,
我々は二つの結論に達している:自然数のセットと平方数のセットは同じサイズであり、そして、自然数のセットと平方数のセットは同じサイズではありません。 それは矛盾しています。
ガリレオは、私たちが矛盾に達した理由は、実際の無限があると仮定したためであると主張しています。 したがって、彼は実際の無限は存在しないと結論づけている。
8.2間接証明
私たちのロジックは、いくつかの有効な引数を証明するのに十分な強さではありません。 例として次の引数を考えてみましょう。,
(P→(QvR))
Q
R
P
この引数は有効に見えます。 私たちが知っている最初の前提によって:Pが真であれば、(Q v R)も真になります。 しかし、QまたはRまたは両方が真になります。 そして、第二および第三の前提によって、我々は知っている:Qは偽であり、Rは偽である。 したがって、(Q v R)が真であることはできず、したがってPが真であることはできません。
真理値表を使って引数をチェックできます。 当社のテーブルは複雑での一つの前提が含まれているからです。,
In any kind of situation in which all the premises are true, the conclusion is true., つまり、前提はすべて最後の行でのみ真です。 その行については、結論も真です。 したがって、これは有効な引数です。
しかし、分を取ると、この引数を証明しようとします。 私たちはで始まります

そして今、私たちは停止しています。 私たちは、私たちのルールのいずれかを適用 ここでは、推論システムを証明するのに十分な強さにしていないという有効な議論があります。
この問題を修正し、推論システムを十分に強くするにはいくつかの方法があります。, 最も古い解決策の一つは、伝統的に不条理への還元を意味する”reductio ad absurdum”と呼ばれる新しい証明方法を導入することです。 この方法は、しばしば”間接証明”または”間接導出”とも呼ばれます。
アイデアは、私たちが結論を否定し、矛盾が生じることを示すということです。 ある文Γとその否定Γを証明するとき,矛盾が示される。 これは任意の文です。 要点は、二価の原則を考えると、私たちは何か誤ったことを証明しなければならないということです。 たとえば、Μが真であればΜは偽であり、Μが真であればΜは偽である。, どちらが偽であるかを知る必要はありません(ΘまたはΘ)。
私たちは論理システムを構築して、真のステートメントから虚偽を生成できないようにしていることを忘れないでください。 したがって、間接的な派生で私たちが生み出す虚偽の原因は、私たちが議論に加えた虚偽でなければなりません。 そして、私たちが議論に加えたのは、結論の否定です。 したがって、結論は真実でなければならない。,
引数の形状は次のようになります。

伝統的に、間接導出の仮定は一般に”還元の仮定”とも呼ばれています。
具体的な例として、私たちは当惑するケースを証明することができます。

4行目の結論を否定するものとしました。 私たちが正しいと信じていた結論はPであり、これの否定はPです。7行目で、私たちはRを証明しました。, 技術的には、その時点で完了しましたが、私たちの証明を理解しようとしている人に親切にしたいので、3行目を繰り返して、文RとRが並んでいるようにし、何かが間違っていることを非常に簡単に見ることができます。 つまり、RとRの両方を証明した場合、何か誤りがあることが証明されました。
私たちの推論はこのようになります。 何が悪かったの? 8行目は繰り返しの正しい使用です;7行目はmodus tollendo ponensの正しい使用から来ています;6行目はmodus ponensの正しい使用から;5行目は二重否定の正しい使用か, だから、私たちは私たちの推論に間違いを犯しませんでした。 私たちはライン1、2、3を使用しましたが、それらは私たちが正しいと仮定することに同意した前提です。 これは4行目を残します。 それが私の矛盾の原因に違いありません。 それは偽であるに違いない。 4行目がfalseの場合、Pはtrueになります。
一部の人々は、間接証明を直接証明よりも強くないと考えています。 これには多くの、そして複雑な理由があります。 しかし、私たちの命題論理のために、これらの理由のどれも適用されません。 これは、私たちの命題論理が一貫していることを証明することが可能であるためです。, これは、システムに最初に虚偽を導入しない限り、命題論理が虚偽を証明できないことを証明することが可能であることを意味する。 (一般に、より強力で高度な論理システムまたは数学システムがそれらのシステムの内部から一貫していることを証明することは不可能である。)命題論理の一貫性が確かであることを考えると、命題論理において間接的な証明が良い推論の形であることを確信することができる。, そして、間接導出の仮定を除いて、証明の他のすべての仮定(すなわち前提)について自信があるならば、間接導出の仮定が虚偽の原因でなければならないと確信することができる。
ここでは用語に関する注意が必要です。 “矛盾”という言葉は、ほとんどの論理の議論であいまいに使用されます。 上記のように、二つの文が主張されており、これらの文が両方とも真実ではない状況を意味することができます。, または、それは真実ではない単一の文を意味することができます。 そのような文の例は(P^P)です。, この文の真理値表は次のとおりです。
| P | P | (P^P) | |
|---|---|---|---|
| t | f | f | |
| f | t | f |
したがって、pの意味にかかわらず、この種の文は決して真実ではありません。,
あいまいさを避けるために、このテキストでは、真ではない単一の文を常に”矛盾した文”と呼びます。 したがって、(P^P)は矛盾した文です。 二つの文が両方とも真実ではないと主張される状況は、”矛盾”と呼ばれます。
8.3この例とその他の例
ガリレオの引数のバージョンを再構築できます。 次のキーを使用します。
P:実際の無限大(自然数と平方数を含む)があります。,
Q:自然数と正方形の数の間に一対一の対応があります。
R:自然数のセットのサイズと平方数のセットのサイズは同じです。
S:すべての正方形の数は自然数です。
T:自然数のいくつかは正方形の数ではありません。
U:平方数よりも多くの自然数があります。,
このキーを使用すると、引数が翻訳されます:
(P→Q)
(Q→R)
(P→(S^T))
((S^T)→U)
P
これが間接導出を使用して有効な引数であることを証明することができます。
iv id=””iv id=””iv id=””iv id=””
6行目では、ガリレオがPを信じ、pを証明することを目的としていたため、pと仮定しました。 この偽りは他の偽りにつながり、それ自体を暴露するでしょう。,
興味のある人のために:ガリレオは、実際の無限大はないが、潜在的な無限大があると結論づけました。 したがって、彼は推論しました、すべての自然数が存在するとは限りません(ある意味で”存在する”)が、自然数を永遠に数えることができるのは事実です。 ガリレオの前後の多くの哲学者はこの見解を保持していました;それはガリレオのほぼ二千年前に書いた重要な論理学者で哲学者だったアリストテレスが持っていた見解に似ています。,
このような議論では、間接的な導出の仮定ではなく、むしろ前提の一つが矛盾の原因であると推論することができることに注意してください。 今日、ほとんどの数学者はガリレオの議論についてこれを信じています。 集合論の発明者であるゲオルク-カントール(1845-1918)という論理学者で数学者は、無限集合は同じサイズの適切な部分集合を持つことができると主張した。, すなわち、カントールは上記の前提4を否定した:すべての平方数が自然数であり、すべての自然数が平方数ではないにもかかわらず、これら二つの集合が異なるサイズであるとは限らない。 しかし、カントールは上記の前提2を受け入れており、したがって、自然数の集合の大きさと平方数の集合の大きさは同じであると信じていた。 今日、カントールの推論を用いて、数学者と論理学者は無限を研究し、無限の性質についての知識の大きな体を開発してきました。 これに興味がある場合は、17.5項を参照してください。,
間接的な導出を説明するための別の例を考えてみましょう。 非常に有用な定理の集合は、今日、論理学者Augustus De Morgan(1806-1871)にちなんで”De Morganの定理”と呼ばれています。 第9章までこれらを完全に述べることはできませんが、英語で同等のものを述べることができます。DeMorganは、(PvQ)と(P^Q)が同等であり、(P^Q)と(PvQ)が同等であること これを考えると、それは((PvQ)→(P^Q))という私たちの言語の定理でなければなりません。 これを証明しよう
式全体が条件付きであるため、条件付き導出を使用します。, したがって、証明は始まらなければなりません。
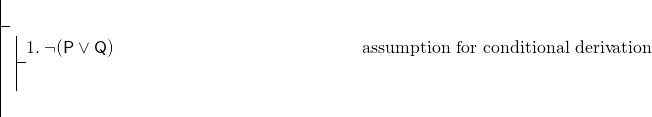
条件付き導出を完了するには、(P^Q)を証明する必要があります。 これは接続詞であり、接続詞を示すための私たちのルールはadjunctionです。 このルールを使用することが(P^Q)を表示する最良の方法かもしれないので、pを表示してからQを表示し、次にadjunctionを実行することを目指すことができ しかし、明らかに作業することはほとんどありません—否定である行1だけです。 そのような場合、通常、間接的な証明を試みることが賢明です。 Pの間接的な証明から始めます。,

これで、矛盾—矛盾を見つける必要があります。 しかし、すでに明らかなものがあります。 1行目は、PもQも真ではないことを示しています。 しかし、3行目はPが真であると言います。 この矛盾を公式とその否定を見つけることによって明示的にする必要があります。 ることができま使用します。

証明を完了するために、この戦略を再び使用します。

ド-モルガンの定理を第9章の問題として証明します。,
証明を行うための一般的な経験則は次のとおりです:条件付きを証明するときは、常に条件付き導出を行います。
8.4問題
- 以下の証明を完成させます。 それぞれに間接的な派生が必要です。 最後の二つは挑戦しています。li>
- 以下の定理を証明してください。(P^P)
- (P^P)
((P→P)^(P→P))であることがわかります。(P→(P^Q))。((P^Q)→(P→Q))。
- 通常の口語英語では、少なくとも二つの前提で独自の有効な引数を書きます。, あなたの議論は単に段落でなければなりません(文の順序付けられたリストや正式な論理のようなものではありません)。 それを命題論理に変換し、間接的な導出を使用してそれが有効であることを証明する。
ガリレオの本のタイトルのこの翻訳は最も一般的になっていますが、より文字通りのものは数学的言説とデモンストレーションでした。 この本の翻訳には、Drake(1974)が含まれます。