生存データの回帰モデル
生存データのカプラン–マイヤー曲線の計算方法について以前に書いた。 ノンパラメトリック推定器として、データセットの生存曲線を簡単に見るのに適しています。 しかし、それがあなたを許さないのは、共変量が生存に及ぼす影響をモデル化することです。 この記事では、生存データに最も使用されているモデルの一つであるCox比例ハザードモデルに焦点を当てます。
推定値の計算方法についていくつか詳しく説明します。, 見積もりは失敗の順序にのみ依存し、実際の時間には依存しないことがわかるので、これは価値があります。 また、生存分析に特別な因果推論に関するいくつかのトリッキーな問題について簡単に議論します。
私たちは通常、以下のような生存曲線の観点から生存データについて考えます。,
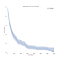
x軸では、日数で時間があります。 Y軸上には、その時点までに”生き残っている”人口の被験者の割合(技術的には割合)があります(推定量)。 生き残ることは比喩的または文字通りです。, それは、人々が一定の年齢まで生きているかどうか、機械が壊れずに一定の時間を作るかどうか、または誰かが仕事を失った後に一定の時間失職しているかどうかかどうかである可能性があります。
重要なことに、生存者分析の合併症は、一部の被験者が”死”を観察していないことである。 彼らがまだ生きていると、機械がまだ上手に機能していることが示され、誰かが失時のデータを収集します。, このような観察は”右検閲”と呼ばれ、検閲を扱うことは、生存分析にはさまざまな統計ツールが必要であることを意味します。
生存者関数を時間の関数であるSとして表します。 (再び、それは技術的に0と1の間の割合ですが、私は同じ意味で二つの単語を使用します)。 簡単にするために、我々は十分に長く待つと、すべての被験者が”死ぬ”という技術的な仮定をするでしょう。”
私たちは、iまたはjのような添字で被験者をインデックス付けします。, 母集団全体の故障時間は、時間変数tに同様の添字で示されます。

iv id=”dfab1f8a80考慮すべきもう一つの微妙なことは、時間を離散的(週ごとの週、たとえば)または連続として扱っているかどうかです。 哲学的に言えば、私たちは離散的な増分で時間を測定するだけです(たとえば、最も近い秒まで)。, 一般的に、私たちのデータは、誰かが特定の年に死亡した場合、または特定の日にマシンが故障した場合にのみ私たちに伝えます。 私はできるだけ明確な博覧会を維持するために離散的および連続的な場合の間を行ったり来たりします。
共変量の影響(例えば、年齢、性別、人種、機械製造業者)をモデル化しようとするとき、我々は通常、共変量がハザード率に及ぼす影響を理解することに興味 ハザード率は、与えられた時間tにおける障害/死/状態遷移の瞬間的な確率であり、すでにその長い間生き残っていることを条件としています。, それをσ(t)と表記する。 時間を離散として扱う:
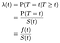
ここで、fは時間tにおける失敗の全体的な確率密度であり、確率密度”関数”にデルタ関数を許可することによって、離散的および連続的場合を統一することができる。 したがって、結果φ=f/Sは連続の場合と同じです。
例を修正しましょう。, 薬物が最初に病気を寛解させる臨床試験の文脈を考えてみましょう。 私たちは、病気が被験者のために進行し始めるときに、薬物が被験者のために”失敗する”と言うでしょう。 最後に、被験者の疾患状態が毎週測定されると仮定します。 次に、λ(3)=0.1の場合、それは10%の確率があることを意味し、特定の被験者にとって、3週目までにまだ寛解している場合、3週目に病気が進行し始める。 残りの90%は寛解のままです。,
次に、全体の確率密度関数fは、時間に関するSの導関数にすぎません。 (繰り返しますが、時間が離散的な場合、fはいくつかのデルタ関数の合計に過ぎません)。,341fa8b2″>
これは、ハザード関数を知っていれば、Sに対してこの微分方程式を解くことができることを意味します。
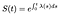
時間が離散的な場合、デルタ関数の合計の積分は、離散時間ごとにハザードの合計に変わります。,
さて、それは私たちが必要とする表記法と基本的な概念をまとめます。 モデルの議論に移りましょう。
非パラメトリックモデル、セミパラメトリックモデル、フルパラメトリックモデル
先ほど述べたように、通常はハザード率λのモデル化に興味があります。
ノンパラメトリックモデルでは、σの関数形式については仮定しません。 Kaplan-Meier曲線は、この場合の最尤推定量です。 欠点は、これにより共変量の効果をモデル化することが困難になることです。 これは、共変量の効果を理解するために散布図を使用するのと少し似ています。, 線形回帰のような完全なパラメトリックモデルほど役に立つとは限りません。
完全パラメトリックモデルにおいて,σの正確な関数形式を仮定した。 完全なパラメトリックモデルについての議論は、それ自体の完全な記事ですが、非常に簡単な議論の価値があります。 以下の表は、最も一般的な完全パラメトリックモデルの三つを示しています。 それぞれの一般化により、次から1 2 3パラメータ。 ハザード関数の関数形式は、中央の列に示されています。 ハザード関数の対数も最後の列に示されています。, 一般化されたワイブル分布(ワイブル分布を再現する)においてσが0であることを除いて、すべてのパラメーター(σ、α、σ)は正であると仮定されます。

対数を見ると、指数モデルはハザード関数は一定である。 ワイブルモデルは、α>1の場合は増加し、α=1の場合は定数であり、α<1の場合は減少すると仮定しています。, 一般化されたワイブルモデルは、ワイブルモデルと同じ方法で開始されます(開始時ln S=0)。 その後、余分なtermⅱが始まります。
これらのモデルの問題は、データについて強い仮定をしていることです。 特定の状況では、これらのモデルが適切であると信じる理由があるかもしれません。 がこれらのその他の複数のオプションが強いというリスクの描画誤った結論によりmisspecificationのモデルです。
これが、セミパラメトリックモデルであるCox比例ハザードが非常に人気がある理由です。, ハザード関数の形状に関する関数型の仮定は行われず、代わりに共変量のみの効果に関する関数型の仮定が行われます。,
Cox比例ハザードモデル
Cox比例ハザードモデルは、通常、時間t、共変量ベクトルx、係数ベクトルβに関して
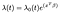
ここで、λは時間の任意の関数であり、ベースラインハザードです。 Xとβの内積は、標準的な線形回帰のように指数で取られます。, 共変量の値にかかわらず、すべての被験者は同じベースラインハザードσを共有します。 その後、共変量に基づいて調整が行われます。
結果の解釈
cox比例ハザードモデルをデータに当てはめた分とします。
- 各被験者の時間を指定する列
- 被験者が”観察された”かどうかを指定する列
- 値が1の場合、被験者はその疾患の進行があったことを意味します。, 0の値は、最後の観察時間で、疾患が進行していなかったことを意味します。 観察は検閲された。
- 共変量Xの列
近似の後、βの値を取得します。 たとえば、簡単にするために、単一の共変量があるとします。 Β=0.1の値は、共変量が1の量だけ増加すると、任意の時点で疾患の進行の可能性が約10%高くなることを意味します。, 正確な値は実際には

βの値が小さい場合、β自体の値はハザードの正確な増加のかなり良い近似です。 Βの値が大きい場合は、正確な量を計算する必要があります。
β=0.1を表現する別の方法は、xが増加するにつれて、xの増加あたり10%の割合でハザードが1増加するということです。 より大きい10.,52%は複利と同じように(連続的な)混合から、ちょうど起こる。
また、β=0は効果がないことを意味し、β負は共変量が増加するほどリスクが少ないことを意味します。 標準的な回帰とは異なり、切片の項は存在しないことに注意してください。 代わりに、切片はベースラインハザードσに吸収され、これも推定することができます(下記参照)。
最後に、ベースラインハザード関数を推定したと仮定すると、サバイバー関数を構築できます。,
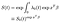
ベースライン関数は、共変量。 通常の線形回帰における切片項の役割を大まかに果たすベースライン生存者関数の解釈には、いくつかの注意が必要です。 共変量が中央に配置されている場合(平均0)、それは”平均”対象の生存者関数を表します。,
Cox比例ハザードモデルの推定
1970年代、イギリスの数学者David Coxは、ベースラインハザードγを推定することなくβを推定する方法を提案しました。 再び、ベースラインハザードを推定できます。 先に述べたように、私たちは、それが時そのものではなく、重要な観察された失敗の順序であることを見るでしょう。
見積もりに飛び込む前に、関係について議論する価値があります。 通常、データを離散的な増分でのみ観測しているため、二つの障害が同時に発生する可能性があります。, たとえば、同じ週に二つのマシンが故障する可能性があり、記録は週単位でのみ行われます。 これらの関係は、多くの洞察を追加することなく、状況の分析をかなり複雑にします。 したがって、私は関係がない場合の推定値を導出します。
私たちのデータは離散時間におけるいくつかの失敗の観測からなることを思い出してください。 私たちの研究の被験者が時間tの前に失敗した(例えば、病気が進行した)場合、それらは”危険にさらされていません。,”また、私たちの研究の被験者が時間tより前の時点で観察を打ち切った場合、それらも危険にさらされていません。”
通常の方法では、尤度関数(共変量と係数を与えられたデータを観測した確率はどれくらいですか)を構築し、それを最適化して最尤推定量を得
被験者jの障害を観察した各離散時間について、障害が発生したと仮定すると、その発生確率は以下のとおりである。 合計は、時間jで危険にさらされているすべての被験者に引き継がれます。,

ベースラインハザードσが脱落したことに注意してください! 非常に便利です。 このため、私たちが構築する尤度は部分的な尤度に過ぎません。 また、時間がまったく表示されないことに注意してください。, 被験者jの用語は、被験者が時間jでまだ生きているかにのみ依存し、被験者が検閲されるか、失敗することが観察される順序にのみ依存します。
部分的な尤度はもちろん、これらの用語の単なる積であり、私たちが観察する各失敗に対するものです(打ち切られた観測値の項はありません)。,
対数部分尤度は次のようになります
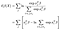
近似は、たとえばpythonパッケージstatsmodelsのような標準的な数値法で行われ、推定値の分散共分散行列はフィッシャー情報行列の逆 何もしなく。,
ベースライン生存者関数の推定
係数を推定したので、生存者関数を推定できます。 これはKaplan–Meier曲線を推定するのと非常によく似ています。時間iにおいて、ベースライン生存者曲線は、時間iにおいて失敗するリスクのある被験者の割合を表す割合αだけ減少すべきである。, つまり、
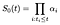
αの最尤推定量を計算するために、αの尤度寄与を考慮します。時間iで失敗した被験者については、確率は、時間iで生きている確率から、次回i+1で生きている確率を少なくすることによって与えられます。
時間iで失敗した被験者については、確率は、時間iで生きている確率から与えられます。 (一時的に時間が注文されていると仮定します)。,
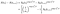
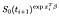
観察された被験者からの余分な用語があります(つまり、検閲されるのではなく失敗することが観察されます)。, 対数尤度は次のようになります
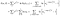
私はエンドポイント(i対i+1)を追跡することについて少しずさんでしたが、それはすべてうまくいくでしょう。
失敗することが観察された被験者にはα項しかありません。, Α-jに関して微分し、関係がないと仮定すると、時間jで生きている被験者に対してのみ左の合計からの寄与を得、右の項からの単一の寄与を得る。,qual to0は、失敗することが観察された各被験者について、いくつかの方程式の解としてβの推定値を使用してαの最尤推定値を得ることができることを意味します。
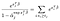
拡張と注意点
cox比例ハザードモデルについて言うことはもっとたくさんありますが、私は物事を簡単に保ち、いくつかのことについて言及しようとします。,
たとえば、時変回帰子を考慮することができ、これは可能です。
心に留めておくべき他の重要なことは、可変バイアスを省略しています。 標準的な線形回帰では、リグレッサと無相関の省略された変数は大きな問題ではありません。 これは生存分析では真実ではありません。 データに同じサイズのサンプリングされたサブ集団があり、それぞれ一定のハザード率を持ち、一方が0.1で他方が0.5であるとします。 最初は、高いハザード率(平均、わずか0.3)が表示されます。, 時間が経つにつれて、ハザード率の高い人口は人口を離れ、ハザード率は0.1に向かって低下することが観察されます。 これら二つの集団を表す変数を省略すると、ベースラインハザード率はすべて台無しになります。