コンテンツ-確率密度関数

コンテンツ

確率密度関数

連続確率変数\(X\)の確率密度関数(pdf)\(f(x)\)は、累積分布関数\(F(x)\)の導関数として定義されます。

\

これは、pdf\(f(x)\)に関して累積分布関数\(F(x)\)を考えることが有用であることがあります。

\

pdf\(f(x)\)は二つの重要な性質を持つ：

1. \(f(x)\geq0\)、すべての\(x\)
2. \(\displaystyle\Int_{-\infty}^{\infty}F(x)\;dx=1\)に対して。,

pdfには無限の種類の形状が可能です。 Pdfは、一つまたは複数のピークを有していてもよいし、まったくピークを有していてもよく、不連続性を有していてもよいし、関数の組み合わせで構成され 図5は、単一のピークと軽度の歪度を持つpdfを示しています。 典型的なpdfの場合と同様に、関数の値は\(x\to\infty\)および\(x\to-\infty\)のようにゼロに近づきます。

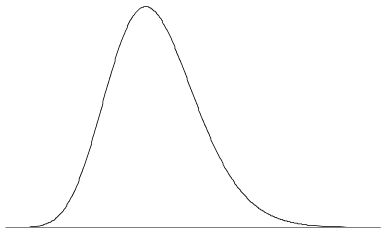
図5:pdfは次のようになります。,

ここで、連続確率変数\(X\)に関する確率がそのpdfにどのように関連しているかを調べます。 ここで重要な結果は、

\_a^b.\]

この結果は、両側が\(F(b)-F(a)\)に等しいという事実に従います。

ノート。

• 連続確率変数については、それが区間にある確率を考慮する必要があります。 この結果の重要性は、確率を見つけるために、与えられた間隔でpdfの下の領域を見つける必要があることを教えてくれるということです。
• pdfの下の総面積は1に等しい。, したがって、この結果は、確率変数が与えられた区間にある確率を近似するために、区間の終わりの間のpdfの下の領域の割合を推測するだけであることを示しています。
• この結果は、pdfが負になることができない理由についての別の視点を提供します。
• pdfは、離散確率変数の確率関数（pf）に類似していますが、それとは異なります。 Pfは確率を与えるので、それよりも大きくすることはできません。, しかし、pdf\(f(x)\)は、\(x\)の値ではなく、確率を表す曲線の下の領域であるため、\(x\)のいくつかの値に対しても大きな値を与えることがあります。 一方、曲線の高さは相対確率を反映しています。 \(F(b)=2f(a)\)ならば、\(b\)の近くの観測は\(a\)の近くの観測とほぼ倍の確率である。,

次のページ-コンテンツ-連続確率変数の平均と分散