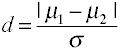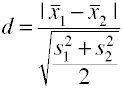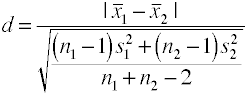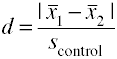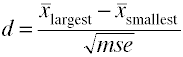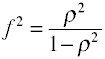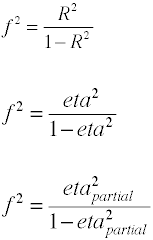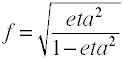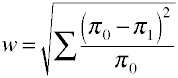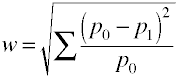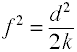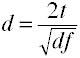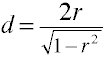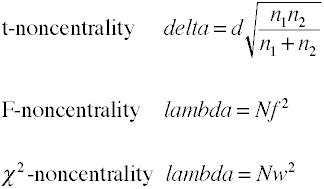効果サイズの一つの使用は、サンプルサイズに依存せず、母集団間の差の大きさまたは説明変数と応答変数の間の関係を定量化する標準化されたインデックスとしてです。 効果サイズのもう一つの使用は、パワー分析。
平均の違いに対する効果サイズ
平均の違いに対する効果サイズは、以下に示すように、コーエンのdは母集団の平均(μs)および母集団標準偏差(μ),
コーエンのdファミリー内の複数のバリアントにつながるサンプルデータからσを推定できるいくつかの異なる方法があります。
二乗平均平方根標準偏差を使用して
プールされた標準偏差(ヘッジのg)を使用して
このバージョンのコーエンのdは、プールされた標準偏差を使用しており、ヘッジのgとも呼ばれています。,
この値は、二乗平均平方根誤差とも呼ばれる平均平方誤差の平方根を取ることによって、anovaプログラムから簡単に取得できます。対照群の標準偏差を使用するコーエンのdの別のバージョンは、対照群の標準偏差を使用するグラス’Δとしても知られている。,
より多くのその後二つのグループ
より多くのその後二つのグループがある場合、最大と最小の差を使用します平均二乗誤差の平方根で割った
回帰分析におけるF比の効果サイズ
OLS回帰における効果サイズの尺度はFであり、Cohenによって次のように定義される。,
ここでも、サンプルデータから効果サイズを計算できるいくつかの方法があります。 注φ2はR2の別の名前です。
分散分析におけるF比の効果サイズ
分散分析に使用される効果サイズは、母集団,
コーエンのfは上記のように定義されていますが、通常はf2の平方根を取って計算されます。
分割表からのσ2の効果サイズ
もう一度、母集団の値に関する定義式から始めます。効果サイズwは、標準化されたカイ二乗統計量の平方根です。,
サンプルデータを使用してwを計算する方法は次のとおりです。
ここでは、低、中、高の効果の推奨値の表です(Cohen、1988)。 これらの価値は絶対に取られるべきではなく、あなたの研究プログラムの文脈の中で解釈されるべきです。 大きな効果の値は、実際にはCohenのdが1.0より大きい値で頻繁に超えられます。,しかし、将来の電力解析に非常に大きな効果サイズを使用することは、おそらく電力不足の研究につながる可能性があるため、お勧めできません。,式
ここで、k=グループの数
二つの独立したグループのためにtをdに変換します
二つの独立したグループのrをdに変換します
非心性推定値
解析法を使用した電力解析には、基本的に効果サイズにサンプルサイズ係数を掛けた非心性。, ここでは一部の関数を推定するnoncentrality.
パワー解析の例
ここでは、パワー解析における効果サイズと非心度をまとめた例を示します。
三つのグループ(k=3)を持つ分散の一方向分析を考えてみましょう。 Andeta2が等しいことを期待するならば。,12この場合、効果サイズは
effect size f = sqrt(eta2/(1-eta2)) = sqrt(.12/(1-.12)) = .369
投影されたサンプルサイズが60の場合、非心の推定値は
noncentrality coefficient lambda = N*f = 60*.369^2 = 60*.136 = 8.17
分子自由度はk-1=3-1=2、分母dfはN-k=60-3=57です。2および57自由度のFの臨界値は3.16です。 これにより、
power = noncentralFtail(df1,df2,lambda,Fcrit(2,57)) = noncentralFtail(2,57,8.17,3.16) = .703
したがって、nは60、効果サイズです。369:以下、名無しにかわりまして7.
私たちはの力を向上させることができます。7投影されたサンプルサイズ75の代わりに60を使用します。, 同じ効果のサイズを使っての。369、我々はの新しい非心性推定値を取得します
noncentrality coefficient lambda = N*f = 75*.369^2 = 75*.136 = 10.2
分子の自由度は同じままですが、分母dfはN-k=75-3=72に等しくなりました。2および72自由度のFの臨界値は3.12です。 今回のパワーは
power = noncentralFtail(df1,df2,lambda,Fcrit(2,72)) = noncentralFtail(2,72,10.2,3.12) = .807
これは許容可能な研究限界内です。
異なるstatパッケージは、noncentralFtailを呼び出す関数で異なる名前と異なる引数の順序を使用することに注意してください。 あなたはあなたのソフトウェアに付属しています。,
ベッカー、L.心理学590コースノート。 Viewed19Jun2009<http://web.uccs.edu/lbecker/Psy590/es.htm>
Cohen,J.1988. 行動科学のための統計的検出力分析。 ヒルズデール、ニュージャージー州:ローレンスアールバウムアソシエイツ