α係数は、応用研究における信頼性を推定するために最も広く使用されている手順です。 Sijtsma(2009)によって述べられているように、その人気は、CRONBACH(1951)がDNA二重らせんの発見に関する記事よりも頻繁に参照として引用されているようなものです。, それにもかかわらず、その限界はよく知られている(Lord and Novick、1968;Cortina、1993;Yang and Green、2011)、最も重要なのは、相関のない誤差、タウ等価性および正規性の仮定である。
無相関誤差の仮定(任意のペアの項目の誤差スコアは無相関である)は、古典的なテスト理論(Lord and Novick、1968)の仮説であり、この複雑さを考慮した推定手順を必要とする複雑な多次元構造の存在を意味する可能性がある(例えば、Tarkkonen and Vehkalahti、2005;Green and Yang、2015)。, スケールが一次元的であればその値が高くなるため、α係数が一次元性の良い指標であるという誤った信念を根絶することが重要です。 実際には、Sijtsma(2009)によって示されているように、正反対のケースであり、そのような条件でのその適用は、信頼性が大きく過大評価される可能性がある(Raykov、2001)。 したがって、αを計算する前に、データが一次元モデルに適合することを確認する必要があります。
タウ等価性の仮定(すなわち, すべてのテスト項目に対して同じ真のスコア、または階乗モデルにおけるすべての項目の因子負荷量が等しい)は、αが信頼性係数と等価であるため タウ等価性の仮定に違反すると、真の信頼性値は過小評価され(Raykov、1997;Graham、2006)、違反の重力に応じて0.6から11.1%の間で変化する可能性がある(Green and Yang、2009a)。 この仮定に従うデータを扱うことは、一般的に実際には実行可能ではありません(Teo and Fan、2013)。,、異なる要因の負荷)がより現実的です。
多変量正規性の要件はあまり知られておらず、パント信頼性推定と信頼区間を確立する可能性の両方に影響を与えます(Dunn et al., 2014). Sheng and Sheng(2012)は、分布が歪んでいる場合および/またはleptokurticである場合、係数αを計算すると負のバイアスが生成されることを最近観察しました。Green and Yang(2009b)は、信頼性の推定における非正規分布の影響の分析において同様の結果を示しました。, 歪度問題の研究は、実際には研究者が歪んだスケールで習慣的に作業することがわかるときにより重要です(Micceri、1989;Norton et al.,2013;Ho and Yu,2014). 例えば、Micceri(1989)は、能力の約2/3と心理測定尺度の4/5以上が少なくとも中等度の非対称性(すなわち、1周りの歪度)を示したと推定した。 それにもかかわらず,信頼性推定に対する歪度の影響はほとんど研究されていない。,
α係数の限界とバイアスに関する豊富な文献(Revelle and Zinbarg、2009;Sijtsma、2009、2012;Cho and Kim、2015;Sijtsma and van der Ark、2015)を考慮すると、これらの限界を克服する代替係数が存在する場合、研究者 これは、前世紀に開発された信頼性を推定するための手順の過剰が議論をoscuredている可能性があります。 これは、この係数の計算の単純さと商用ソフトウェアにおけるその可用性によってさらに悪化していたでしょう。,
pxx’信頼性係数を推定することの難しさは、その定義pxx’=σt2σx2にあり、これは本質的に観察できない場合の分散分子の真のスコアを含みます。 Α係数は、アイテムまたはコンポーネント間の共分散からこの観測不可能な分散を近似しようとします。 Cronbach(1951)は、タウ等価性がない場合、α係数(またはαと等価であるGuttman”s lambda3)が良い下界近似であることを示した。, 実際、この名前は理論的角度からの最良の近似である最大下界法(GLB)に与えられている(Jackson and Agunwamba,1977;Woodhouse and Jackson,1977;Shapiro and ten Berge,2000;Soşan,2000;ten Berge and Soşan,2004;Sijtsma,2009)。 しかしながら、RevelleとZinbarg(2009)はωがGLBよりも良い下限を与えると考えている。, したがって、これら二つの方法のどれが最良の下限を与えるかについては未解決の議論があり、さらに非正規性の問題は網羅的に調査されていない。
ω係数
McDonald(1999)は、階乗解析フレームワークから信頼性を推定するためのwt係数を提案しました。
ここで、θjは項目jの負荷、θj2は項目jの共通性、θは一意性に等しい。, Wt係数は、その式にラムダを含めることにより、タウ等価性(すなわち、すべての試験項目の等しい因子負荷)が存在する場合(wtは数学的にαと一致する)、および構成の表現に異なる識別を持つ項目が存在する場合(すなわち、項目の異なる因子負荷:同族測定)の両方に適している。 したがって、wtは、タウ等価性の仮定に違反したときにαの過小評価バイアスを補正する(Dunn et al.,2014)および異なる研究は、それが信頼性を推定するための最良の選択肢の一つであることを示している(Zinbarg et al.,,2005,2006;Revelle and Zinbarg,2009),これまで歪度の条件でその機能は不明であるが、.
誤差間に相関が存在する場合、またはデータ内に複数の潜在次元がある場合、説明された全分散に対する各次元の寄与が推定され、多次元データでαの最悪の過大評価バイアスを修正することができる、いわゆる階層ω(wh)を得る(Tarkkonen and Vehkalahti,2005;Zinbarg et al.,2005;Revelle and Zinbarg,2009)., 係数whおよびwtは一次元データでは等価であるため、この係数を単にωと呼びます。
最大下界(GLB)
Sijtsma(2009)は、一連の研究で、信頼性の最も強力な推定量の一つは、古典的なテスト理論(Cx=Ct+Ce)の仮定からWoodhouseとJackson(1977)によってGLB推定され それは、項目真のスコアCtに対する項目間共分散行列の合計と、項目間誤差共分散行列Ce(ten Berge and Soñan,2004)に分解されます。, その式は次のとおりです。
ここで、σx2は検定分散であり、tr(Ce)は推定が非常に困難であることが証明されている項目間誤差共分散行列 一つの解決策は、最小ランク因子分析(glbとして知られている手順)などの階乗手順を使用することでした。fa)。 より最近では、Andreas Moltner(Moltner and Revelle、2015)によって考案されたアルゴリズムからGLB algebraic(GLBa)手続きが開発されています。, Revelle(2015a)によると、この手順はJackson and Agunwamba(1977)による元の定義に最も忠実な形式を採用しており、重要度によって項目を重み付けするベクトルを導入するという追加の利点がある(Al-Homidan,2008)。その理論的強みにもかかわらず、GLBはほとんど使用されていないが、最近のいくつかの経験的研究は、この係数がαよりも良好な結果をもたらすことを示している(Lila et al.,2014)およびαおよびω(Wilcox et al., 2014)., それにもかかわらず、小さなサンプルでは、正規性の仮定の下で、それは真の信頼性値を過大評価する傾向があります(Shapiro and ten Berge、2000);しかし、非正規条件下でのその機能は、特にアイテムの分布が非対称である場合には不明のままである。
上記で定義された係数とそれぞれのバイアスと限界を考慮して、この研究の目的は、タウ等価性とサンプルサイズの仮定を考慮して、非対称項目の存在下でこれらの係数のロバスト性を評価することである。,
メソッド
データ生成
データは、階乗モデルに従って、R(R Development Core Team,2013)およびRStudio(Racine,2012)ソフトウェアを使用して生成されました。
ここで、Xijは項目jにおける被験者iのシミュレートされた応答であり、θjkは因子k(ユニファクトリアルモデルによって生成された)における項目jの負荷であり、fkは標準化正規分布(平均0と分散1)によって生成された潜在因子であり、ejは標準化された正規分布に従う各項目のランダムな測定誤差である。,
偏った項目:標準正規Xijは、Headrick(2002)によって提案された手順を使用して非正規分布を生成するために変換されました:
シミュレートされた条件
信頼性係数(α,ω,GLBおよびGLBa)の性能を評価するために私たちは、三つのサンプルサイズ(250、500、1000)、二つのテストサイズで働いた:短い(6項目)と長い(12項目)、タウ等価の二つの条件(タウ等価を持つものとなし、すなわち、,(すべての項目が正常であることから、すべての項目が非対称であることまで)非対称アイテムの進歩的な組み込み。 短いテストでは、信頼性は0.731に設定され、タウ等価性の存在下では因子負荷量=0.558の六つの項目で達成されます。0.3, 0.4, 0.5, 0.6, 0.7, および0.8(付録Iを参照)。 12項目の長いテストでは、信頼性は0に設定されました。,845は、タウ等価性と同族モデルの両方についての短いテストと同じ値を取る(この場合、ラムダの各値について二つの項目があった)。 このように120条件を数値シミュレーションを実施した1000レプリカ。
データ解析
主な解析は、αおよびωを推定できるPsych(Revelle,2015b)およびGPArotation(Bernaards and Jennrich,2015)パケットを使用して行われました。 GLBの推定には二つのコンピュータ化されたアプローチを用いた。fa(Revelle、2015a)およびglb。,algebraic(Moltner and Revelle、2015)、後者はHunt and Bentler(2015)のような著者によって働いていました。信頼性回復における様々な推定量の精度を評価するために,誤差の二乗平均平方根(RMSE)とバイアスを計算した。 最初は、推定された信頼性とシミュレーションされた信頼性の差の平均であり、次のように定式化されます。
ここで、σ^は各係数の推定信頼度、σはシミュレーションされた信頼性、Nrはレプリカの数です。, %バイアスは、推定された信頼性の平均とシミュレーションされた信頼性の差として理解され、次のように定義されます。
両方の指標では、値が大きいほど推定器の不正確さが大きくなりますが、RMSEとは異なり、バイアスは正または負であり、この場合、係数がシミュレーションされた信頼性パラメータを過小評価または過大評価しているかどうかに関する追加情報が得られます。, Hoogland and Boomsma(1998)の勧告に従って、RMSE<0.05および%bias<5%の値が許容されると考えられていました。
結果
主な結果は、表1(6項目)および表2(12項目)に示されています。 これらは,tau等価条件および同族条件における係数のRMSEおよび%バイアスを示し,非対称項目の徐々の取り込みに伴って検定分布の歪度がどのように増加するかを示した。
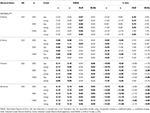
テーブル1., 6つの項目、三つのサンプルサイズおよび歪んだ項目の数について、タウ等価性および同族条件を有するRMSEおよびバイアス。
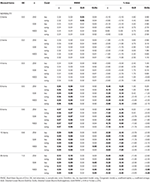
テーブル2. 12項目、三つのサンプルサイズおよび歪んだ項目の数について、タウ等価性および同族条件を持つRMSEおよびバイアス。
タウ等価性と正規性(歪度<0.2)の条件下でのみ、α係数がωのようにシミュレートされた信頼性を正しく推定することが観察されます。, 同属の条件では、ωはαの過小評価を補正する。 GLBとGLBaはどちらも正規性の下で正のバイアスを示しますが、GLBaはGLBよりもおおよそσ小さい%バイアスを示します(表1参照)。 サンプルサイズを考慮すると、テストサイズが大きくなるにつれて、GLBとGLBaの正のバイアスは減少するが、消えることはないことがわかります。
非対称条件では、表1では、αとωの両方がRMSEの増加と過小評価によって許容できない性能を示し、バイアスに達する可能性があることがわかります>α係数の13%(ωの場合は1と2%低い)。, テスト歪度または非対称項目の数が増加すると、GLB係数とGLBa係数はより低いRMSEを示します(表1、2を参照)。 GLB係数は、検定の検定の歪度値が約0.30である場合により良い推定値を示し、GLBaは非常に似ており、0.20または0.30で検定の歪度値を持つωよりも良い推定値を示します。 ただし、歪度の値が0.50または0.60に増加すると、GLBはGLBaよりも優れたパフォーマンスを示します。 テストサイズ(6または12ítems)は、推定値の精度に対するサンプルサイズよりもはるかに重要な効果を持っています。,
ディスカッション
この研究では、四つの要因を操作しました:タウ等価または同族モデル、サンプルサイズ(250、500、および1000)、テスト項目の数(6および12)および非対称項目の数(0非対称項目から非対称であるすべての項目まで)分析された四つの信頼性係数における非対称データの存在に対するロバスト性を評価するために。 これらの結果を以下に論じる。,
タウ等価性の条件では、αとω係数は収束しますが、タウ等価性(同族)がない場合、ωは常にαよりも良い推定値と小さいRMSEと%バイアスを示します。 したがって、このより現実的な条件では(Green and Yang,2009a;Yang and Green,2011)、αは負に偏った信頼性推定量となり(Graham,2006;Sijtsma,2009;Cho and Kim,2015)、ωは常にαよりも好ましい(Dunn et al., 2014). 正規性の仮定に違反しない場合、ωは評価されたすべての係数の最良の推定量です(Revelle and Zinbarg、2009)。,
サンプルサイズに目を向けると、この因子は正規性または正規性からのわずかな逸脱の下で小さな効果を有することがわかります:RMSEとバイアスはサンプルサイズが大きくなるにつれて減少します。 それにもかかわらず、これら二つの係数について、サンプルサイズが250で正規性が比較的正確な推定値を得ると言えるかもしれない(Tang and Cui,2012;Javali et al., 2011)., GLBおよびGLBa係数では、サンプルサイズが大きくなるとRMSEおよびバイアスは減少する傾向がありますが、サンプルサイズが1000の大きい場合でも正規性の条件に対して正のバイアスを維持します(Shapiro and ten Berge,2000;ten Berge and Soñan,2004;Sijtsma,2009)。
テストサイズでは、一般的に6項目のRMSEとバイアスが12よりも高くなり、項目数が高いほどRMSEと推定量のバイアスが低くなることを示唆しています(Cortina、1993)。 一般に、傾向は6項目と12項目の両方に対して維持されます。,これらの結果は、Sheng and Sheng(2012)およびGreen and Yang(2009b)によって見つかったものと同様である。 係数ωはαのものと同様のRMSEとバイアス値を示すが,tau等価性を有していてもわずかに良好である。 GLBとGLBaは、テスト歪度が0に近い値から離れると、より良い推定値を示すことがわかりました。実際には非対称データを見つけることが一般的であることを考慮すると(Micceri、1989;Norton et al.,,2013;Ho and Yu,2014),Sijtsmaの提案(2009)信頼性推定器としてGLBを使用することは十分に確立されているようです。 Revelle and Zinbarg(2009)やGreen and Yang(2009a)のような他の著者はωの使用を推奨しているが、この係数は正規性の条件や歪度項目の割合が低い場合にのみ良好な結果をもたらした。 いずれにせよ,これらの係数はαよりも理論的および経験的利点が大きかった。 それにもかかわらず、我々は研究者に時間厳守推定だけでなく、間隔推定を利用することを推奨する(Dunn et al., 2014).,
これらの結果はシミュレーションされた条件に限定され、誤差間に相関がないと仮定される。 これにより、より複雑な多次元構造(Reise、2012;Green and Yang、2015)を有する様々な信頼性係数の機能を評価し、正規性の仮定に準拠していない順序および/またはカテゴリデータの存在下で、さらなる研究を行うことが必要になるであろう。
結論
合計テストスコアが正規分布している場合(すなわち, これらはGLBによって提示される過大評価の問題を避けるので、ωが最初の選択肢であり、αが続くはずである。 ただし、低または中skewのテスト歪度がある場合は、GLBaを使用する必要があります。 これらの条件下では、サンプルサイズが何であれ、信頼性推定器としてαとωの両方を使用することはお勧めできないため、非対称項目の割合が高い場合にGLBが推奨されます。
著者の貢献
研究と理論的枠組みのアイデアの開発(IT、JA)。 方法論的枠組みの構築(IT、JA)。, R言語構文(IT、JA)の開発。 データ分析およびデータの解釈(IT、JA)。 現在の理論的背景に照らして結果を議論する(JA、IT)。 記事の作成と執筆(JA、IT)。 一般に、両方の著者はこの作品の発展に均等に貢献してきました。,
資金調達
最初の著者は、この記事の研究、原作者、および/または出版のための以下の財政的支援の領収書を開示しました:これは、科学技術研究
利益相反声明
著者らは、この研究が潜在的な利益相反と解釈され得る商業的または財務的関係がない場合に行われたと宣言している。
Cronbach,L.(1951)., 係数アルファおよびテストの内部構造。 サイコメトリカ16,297-334. doi:10.1007/BF02310555
CrossRef Full Text|Google Scholar
McDonald,R.(1999). テスト理論:統一された処置。 ローレンス-アールバウム-アソシエイツ(Lawrence Erlbaum Associates)。
Google Scholar
R開発コアチーム(2013年)。 R:統計計算のための言語と環境。 ウィーン:統計計算のためのR財団。
Raykov,T.(1997)., Scale reliability, cronbach”s coefficient alpha, and violations of essential tau- equivalence with fixed congeneric components. Multivariate Behav. Res. 32, 329–353. doi: 10.1207/s15327906mbr3204_2
PubMed Abstract | CrossRef Full Text | Google Scholar
Raykov, T. (2001). Bias of coefficient alpha for fixed congeneric measures with correlated errors. Appl. Psychol. Meas. 25, 69–76. doi: 10.1177/01466216010251005
CrossRef Full Text | Google Scholar
Revelle, W. (2015b). Package “psych.,”オンラインで利用可能:http://org/r/psych-manual.pdf
Shapiro,A.,and ten Berge,J.M.F.(2000). 最小トレース因子分析の漸近バイアスで、信頼性の下限を最大にするアプリケーションがあります。 サイコメトリカ65,413-425. doi:10.1007/BF02296154
CrossRef Full Text|Google Scholar
ten Berge,J.M.F.,and Soğan,G.(2004). テストの信頼性と単次元性の仮説に対する最大の下限。 サイコメトリカ69,613-625. 土井:10,1007/BF02289858
CrossRef Full Text|Google Scholar
Woodhouse,B.,And Jackson,P.H.(1977). 非均質項目から構成されるテストにおける合計スコアの信頼性のための下限:II:最大の下限を見つけるための検索手順。 サイコメトリカ42,579-591. doi:10.1007/BF02295980
CrossRef Full Text|Google Scholar
Appendix I
Pearsonの相関行列から信頼性係数を推定するためのr構文。, 対角線外の相関値は、項目の因子荷重を掛けることによって計算されます:(1)タウ等価モデルそれらはすべて0.3114に等しい(θi θj=0.558×0.558=0.3114)および(2)同族モデルそれらは異なる因子荷重の関数として変化する(例えば、行列要素a1,2=θ1θ2=0.3×0.4=0.12)。 どちらの例でも、真の信頼性は0.731です。
>オメガ(Cr、1)$アルファ#標準化Cronbach”s α
0.731
>オメガ(Cr、1)$オメガ。tot#係数ω合計
0.,731
> glb.fa(Cr)$glb # GLB factorial procedure
0.731
> glb.algebraic(Cr)$glb # GLB algebraic procedure
0.731
> omega(Cr,1)$alpha # standardized Cronbach”s α
0.717
> omega(Cr,1)$omega.tot # coefficient ω total
0.731
> glb.fa(Cr)$glb # GLB factorial procedure
0.754
> glb.algebraic(Cr)$glb # GLB algebraic procedure
0.731