“私は、とにかく、彼はサイコロを投げないと確信しています。,”
~Albert Einstein
- 確率変数
- 離散確率変数
- 連続確率変数
- 混合確率変数
- 累積分布関数(CDF)
- 確率密度関数(PDF)
- インタラクティブなCDF/PDFの例
確率変数:

あなたのポケットからコインを取り、それを空中に投げることだったとします。 それは宇宙を反転しながら、あなたはおそらくその未来について何を言うことができ
それは頭を上げるのだろうか? テイルズ?, それ以上に、それはどのくらい空気中に残るのだろうか? 何回跳ね返りますか? どこまでで最初にぶつかることから、地上で最後に来ます。 その点では、それは地面に当るか。 今まで残りの部分に来ますか?
そのような質問については、観測のずっと前に答えを解決することができ、解決することができます。 しかし、他の人にとっては、将来について何か役に立つことを言いたいのであれば、判断を持ち、より曖昧な言葉で話すしかありません。,
科学者として、もちろん、有用なもの(または少なくとも権威あるもの)を言うことは私たちの仕事です。..)、重要な物理的なシステムの比喩的なコインはまだ空気中にありますが。 頭や尾は生死の問題かもしれません。 私たちのコインは、例えば、原子力発電所における様々な可能な冷却材流量またはウランの質量であってもよい。 私たちは、メルトダウンの代わりにタービンを旋回させる可能性があることを知っていることを大いに気にしています。,
厳密な決定論者にとって、そのような賭けはすべて、比喩的であろうとなかろうと、コインが鋳造されるずっと前に決済されました。 私たちがコインの投げで適用される力、その正確な質量の分布、部屋の空気のさまざまな微細な動きだけを知っていたならば。.. 私たちがそれをすべて知っていれば、特定のコイントスには100%の着陸の可能性があり、他の結果の可能性はゼロであることがわかります。
しかし、私たちはもちろん、世界のそのような知識の言及できる部分さえも欠けていることがよくあります。, 例えば、ウラン原子がいつ分裂するかを予測する方法はなく、そのような出来事がより大きな世界に影響を与えるならば、そのマクロイベントは本当に予測不可能である。 いくつかの結果は本当に空中にあり、過去の一部になるまで不安定です。
この現実に対処し、システムの将来の状態を何らかの有用な方法で記述できるようにするために、ランダム変数を使用します。, 確率変数は、単にシステムのそれぞれの可能な物理的結果をある一意の実数に関連付ける関数です。 そのため、離散変数、連続変数、混合変数の三種類があります。 以下のセクションでは、これらのカテゴリについて簡単に説明し、例を示します。
離散確率変数:
コイントスをもう一度考えてみましょう。 我々は可能な結果として頭や尾を持つことができます。 変数xをシングルトスの頭の数として定義した場合、xはおそらく1または0になる可能性がありますが、他には何もありません。, このような関数xは、離散確率変数の例となります。 ようなランダム変数できるようにしました離散数値です。 他の例は、妊娠検査の可能な結果、またはクラスルーム内の学生の数であろう。
連続確率変数:
コイントスに戻ると、コインが静止した場所と最初に地面に当たった場所の間の距離を記述したい場合はどうなりますか。 その距離xは、実数の連続範囲内で無限の数の値を取る可能性があるため、連続確率変数になります。, 硬貨は1cm、または1.1cm、または1.11cm、または上と上に移動することができます。 連続ランダム変数の他の例は、私たちの銀河内の星の質量、海水のpH、またはガスクロマトグラフ内のいくつかの分析物の滞留時間であろう。
混合確率変数:
混合確率変数は離散成分と連続成分の両方を持ちます。 このような確率変数に遭遇することはまれです。 ただし、可能な例としては、サンプルの重量を測定し、負の値として測定された重量には0の値が与えられると判断することができます。, このようにして、確率変数はx=0の離散成分とx>0の連続成分を持ちます。
累積分布関数(CDF):
もちろん、ランダム変数を数学的に記述(および視覚的に表示)する方法についての問題が生じます。 これらのタスクには、確率密度関数(PDF)と累積密度関数(CDF)を使用します。 Cdfは離散確率変数と連続確率変数の両方についてPdfよりも理解しやすいので、最初にCdfについて説明します。
公正な6siddedサイコロを投げることを検討してください。, 私たちは、確率変数の可能な値のいずれかを得る1で6のチャンスを持っているでしょう(1, 2, 3, 4, 5, または6)。 これらの可能な値をx軸にプロットし、それぞれの特定の値、x、またはxより小さい値を測定する確率をy軸にプロットすると、確率変数の累積分布関数が得られます。
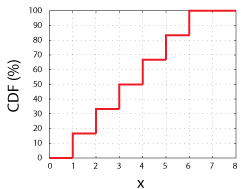
公正な6SiddedサイコロのCDF。 各ステップは16.67%、または1で6の高さであることに注意してください。
この関数CDF(x)は、xまでの任意の値を測定するオッズを単純に示します。, したがって、すべてのCdfはすべて次の特性を持たなければなりません。
- X=-∞の場合、CDFは0に等しくなければならず、xが+∞に近づくにつれて1(または100%)に近づく必要があります。 簡単に言えば、すべての可能な結果のうち、結果がなければなりません;六面サイコロを投げ、-πとπの間の値を得る可能性は100%です。
- 累積分布関数の傾きは、常にゼロ以上でなければなりません。 たとえば、6つのサイコロを投げて(公正かどうか)、0と4の間の値を得る可能性を考えてみましょう。, そのチャンスは、おそらく0と5の間の値を得るチャンスよりも多くすることはできません,1,2,または3着陸フェイスアップのオッズは、もちろん、常に1,2,3,または4を得るオッズのいくつかの割合になるだろうからです.
連続確率変数の例として、次のアプレットは正規分布の累積分布関数を示しています。,div>
| -5 | 5 |
| x | |
This important distribution is discussed elsewhere., 単に、上記で説明し、離散ランダム変数について説明したCDFの特性は、連続ランダム変数についても同様に保持することに注意してください。
Cdfのプロパティのより直感的な例については、以下の対話型の例を参照してください。 また、統計の分野にとって重要で、このサイトで使用されている他の多くのCdfの対話型プロットは、ここにあります。
確率密度関数(PDF):
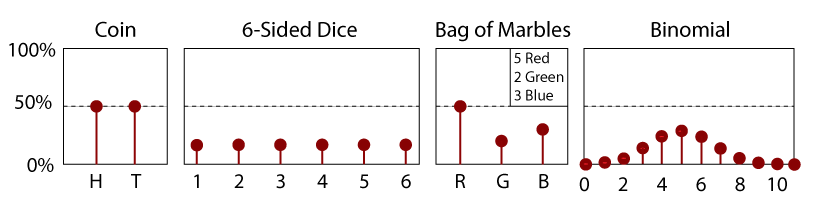
公正な6SiddedサイコロのPDF。
PDFは単にCDFの導関数です。, したがって、PDFは確率変数xの関数でもあり、その大きさは特定の値を測定する相対的尤度を示すものになります。 これはCDFの傾きであるため、PDFは常に正でなければなりません。 さらに、定義により、-∞とxの間のpdf(x)の曲線下の面積は、そのCDF(x)に等しい。 したがって、二つの値x1とx2の間の領域は、その範囲内の値を測定する確率を与えます。
次のアプレットは、正規分布ランダム変数xのPDFの例を示しています。,
Normal PDF
|
x:
| mean:
| stdev:
| f(x):
| |
Notice, when the mean and standard deviations are equal, how the PDF correlates with the normal CDF in the section above., また、連続PDFと離散PDFの違いを考慮してください。 離散PDF(上記のdiceのような)は特定の結果を得る確率を与えますが、連続Pdfの確率は離散ポイントではなく範囲の問題です。 たとえば、PDFで見ることができるように、1in6(16.6%)の確率で3をサイコロで転がすことが明らかにあります。 しかし、上記のように、通常のPDFとゼロの平均を持つ確率変数で正確にゼロを測定する奇数は何ですか? PDFが最も大きい値であっても、正確に0.000000を測定する可能性があります。.,. おそらく直感的にはゼロです。 特定の乱数を無限の精度まで測定する確率は、実際にはゼロです。 連続PDFを使用すると、代わりに、ゼロより大きい確率を得るために二つの値の間で測定するオッズが何であるかを尋ねることができます。 この確率を見つけるには、単に確率変数の累積分布関数を使用します。, 累積分布関数はある値またはその値よりも低い値を測定する奇数を示すので、x1とx2の間で測定する尤度を見つけるには(x1>x2)、x1における累積分布関数の値を取り、そこからx2における累積分布関数の値を引くだけである。 たとえば、上記のアプレットで通常の累積分布関数(λ=0、およびλ=1)を使用すると、0.01と0.02の間の測定のオッズを知りたい場合、CDF(x=0.1)=53.9828%およびCDF(x=0.2)=57.9260%が見つかります。 次に、差CDF(0.2)-CDF(0.1)は、約3.9%のオッズを与えます0.1と0.2の間のxを測定します。, Pdfのプロパティのより直感的で視覚的な例については、以下のインタラクティブな例を参照してください。 また、対話型プロット図の多くの重要なPdf当ウェブサイト上で使用される場合が見られます。 | |||||||||||||||||