콘텐츠 확률 밀도 함수

콘텐츠

확률 밀도 함수

확률 밀도 함수(pdf)\(f(x)\)의 지속적인 임의의 변수를\(X\)으로 정의의 유도체 cdf\(F(x)\):

\

그것은 때때로 고려하는 것이 유용 cdf\(F(x)\)관점에서의 pdf\(f(x)\):

\

pdf\(f(x)\)는 두 개의 중요한 특성.

1. \(f(x)\hra 출력 0\),에 대한 모든\(x\)
2. \(\displaystyle\int_{-\infty}^{\infty}f(x)\;dx=1\).,유일한 요구 사항은 위의 두 속성이기 때문에

pdf 에 대해 무한한 다양한 모양이 가능합니다. Pdf 수 있는 하나 또는 여러 개의 봉우리 또는 피크에 있는 불연속,수의 조합으로 구성되어 함수,그래서. 그림 5 는 단일 피크와 약간의 경미한 왜도를 가진 pdf 를 보여줍니다. 일반적인 pdf 의 경우와 마찬가지로 함수의 값은\(x\to\infty\)및\(x\to-\infty\)로 0 에 접근합니다.

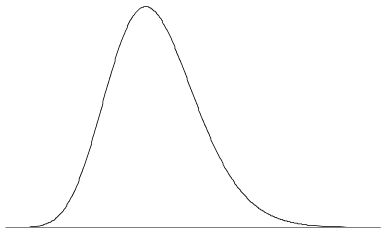
그림 5:pdf 는 다음과 같이 보일 수 있습니다.,

이제 연속 랜덤 변수\(X\)에 관한 확률이 pdf 와 어떻게 관련되는지 살펴 봅니다. 중요한 결과는

\_a^b.\]

이 결과 다음 사실에서는 양쪽이 동일한 것을\(F(b)-F(a)\).

노트.

• 연속 랜덤 변수의 경우,우리는 그것이 간격에있는 확률을 고려해야합니다. 이 결과의 중요성은 확률을 찾기 위해 주어진 간격에서 pdf 아래의 영역을 찾아야한다는 것을 알려줍니다.
• pdf 아래의 총 면적은 1 과 같습니다., 그래서 이 결과를 알려줍니다 우리는 대략적인 확률 무작위 변수에서 주 간격,우리는 단지를 생각해야의 일부 지역에서의 pdf 사이 끝까지 간격입니다.
• 이 결과는 pdf 가 부정적 일 수없는 이유에 대한 또 다른 관점을 제공합니다.
• pdf 는 이산 랜덤 변수에 대한 확률 함수(pf)와 유사하지만 다릅니다. Pf 는 확률을 제공하므로 1 보다 클 수 없습니다., Pdf\(f(x)\),그러나,줄 수 있는 보다 큰 값을 중 하나에 대한 일부의 값\(x\),지 않기 때문에 값의\(f(x)\)그러나 지역에서 곡선을 나타내는 확률입니다. 반면에 곡선의 높이는 상대 확률을 반영합니다. \(F(b)=2f(a)\)인 경우\(b\)근처의 관측치는\(a\)근처의 관측치보다 약 두 배 높습니다.,

다음 페이지 내용의 평균과 분산의 지속적인 랜덤변수