współczynnik α jest najczęściej stosowaną procedurą szacowania niezawodności w badaniach stosowanych. Jak stwierdził Sijtsma (2009), jego popularność jest taka, że Cronbach (1951) był cytowany jako odniesienie częściej niż artykuł o odkryciu podwójnej helisy DNA., Niemniej jednak jego ograniczenia są dobrze znane (Lord and Novick, 1968; Cortina, 1993; Yang and Green, 2011), z których najważniejsze to założenia nieskorelowanych błędów, równoważności tau i normalności.
założenie nieskorelowanych błędów (wynik błędu dowolnej pary elementów jest nieskorelowany) jest hipotezą klasycznej teorii testów (Lord and Novick, 1968), której naruszenie może oznaczać obecność złożonych wielowymiarowych struktur wymagających procedur szacowania, które uwzględniają tę złożoność (np. Tarkkonen and Vehkalahti, 2005; Green and Yang, 2015)., Ważne jest, aby wykorzenić błędne przekonanie, że współczynnik α jest dobrym wskaźnikiem jednowymiarowości, ponieważ jego wartość byłaby wyższa, gdyby skala była jednowymiarowa. W rzeczywistości jest dokładnie odwrotnie, jak wykazano w Sijtsma (2009), a jego zastosowanie w takich warunkach może prowadzić do znacznego zawyżenia wiarygodności (Raykov, 2001). W związku z tym przed obliczeniem α należy sprawdzić, czy dane pasują do modeli jednowymiarowych.
założenie równoważności tau (tj.,, ten sam prawdziwy wynik dla wszystkich elementów testowych lub równe obciążenia współczynników wszystkich elementów w modelu czynnikowym) jest wymogiem, aby α był równoważny współczynnikowi niezawodności (Cronbach, 1951). Jeśli założenie równoważności tau zostanie naruszone, prawdziwa wartość niezawodności zostanie niedoszacowana (Raykov, 1997; Graham, 2006) o kwotę, która może wahać się od 0,6 do 11,1% w zależności od wagi naruszenia (Green and Yang, 2009a). Praca z danymi zgodnymi z tym założeniem jest zasadniczo nieopłacalna w praktyce( Teo and Fan, 2013); model kongeneryczny (tj.,, różne obciążenia czynników) jest bardziej realistyczny.
wymóg normalności wielowariantowej jest mniej znany i wpływa zarówno na ocenę wiarygodności punktowej, jak i możliwość ustanowienia przedziałów ufności (Dunn et al., 2014). Sheng and Sheng (2012) zaobserwowali niedawno, że gdy rozkłady są przekrzywione i/lub leptokurtyczne, ujemne bias jest wytwarzany, gdy współczynnik α jest obliczany; podobne wyniki zostały przedstawione przez Green and Yang (2009b) w analizie skutków rozkładów nienormalnych w szacowaniu niezawodności., Badanie problemów z przekrzywieniem jest ważniejsze, gdy widzimy, że w praktyce naukowcy zwykle pracują z przekrzywionymi skalami(Micceri, 1989; Norton et al., 2013; Ho and Yu, 2014). Na przykład Micceri (1989) oszacował, że około 2/3 zdolności i ponad 4/5 miar psychometrycznych wykazuje co najmniej umiarkowaną asymetrię(tj. skośność około 1). Pomimo tego, wpływ skośności na szacowanie niezawodności nie został zbadany.,
biorąc pod uwagę bogatą literaturę na temat ograniczeń i uprzedzeń współczynnika α (Revelle and Zinbarg, 2009; Sijtsma, 2009, 2012; Cho and Kim, 2015; Sijtsma i van der Ark, 2015), powstaje pytanie, dlaczego naukowcy nadal używają α, gdy istnieją alternatywne współczynniki, które przezwyciężają te ograniczenia. Możliwe, że nadmiar procedur szacowania wiarygodności wypracowanych w ubiegłym stuleciu wywołał dyskusję. Byłoby to jeszcze bardziej spotęgowane przez prostotę obliczania tego współczynnika i jego dostępność w oprogramowaniu komercyjnym.,
trudność oszacowania współczynnika niezawodności PXX polega na jego definicji PXX=σt2∕σx2, która zawiera prawdziwy wynik w liczniku wariancji, gdy jest to z natury nieobserwowalne. Współczynnik α próbuje zbliżyć tę nieobserwowalną wariancję od kowariancji między elementami lub składnikami. Cronbach (1951) wykazał, że przy braku równoważności tau współczynnik α (lub Guttman”s lambda 3, który jest odpowiednikiem α) był dobrym przybliżeniem o niższej granicy., Tak więc, gdy założenia zostaną naruszone, problem przekłada się na znalezienie najlepszej możliwej dolnej granicy; w rzeczywistości nazwa ta pochodzi od największej metody dolnej granicy (GLB), która jest najlepszym możliwym przybliżeniem z teoretycznego kąta (Jackson and Agunwamba, 1977; Woodhouse and Jackson, 1977; Shapiro and ten Berge, 2000; Sočan, 2000; ten Berge and Sočan, 2004; Sijtsma, 2009). Jednak Revelle i Zinbarg (2009) uważają, że ω daje lepszą niż GLB granicę dolną., Istnieje zatem nierozstrzygnięta debata, która z tych dwóch metod daje najlepszą granicę niższą; ponadto kwestia nienormalności nie została wyczerpująco zbadana, co omawia niniejsza praca.
ω współczynniki
McDonald (1999) zaproponował współczynnik WT dla oszacowania wiarygodności na podstawie analizy czynnikowej, który można formalnie wyrazić jako:
gdzie λj jest obciążeniem elementu j, λj2 jest zbiorowością elementu j, A ψ równa się wyjątkowości., Współczynnik WT, poprzez uwzględnienie lambda w swoich wzorach, jest odpowiedni zarówno wtedy, gdy istnieje równoważność tau (tj. równe obciążenia współczynników wszystkich badanych elementów) (WT pokrywa się matematycznie z α), jak i gdy elementy z różnymi rozróżnieniami są obecne w reprezentacji konstrukcji (tj. różne obciążenia współczynników elementów: congenic miary). W związku z tym WT koryguje błąd niedoszacowania α, gdy założenie równoważności tau jest naruszone (Dunn et al., 2014), a różne badania pokazują, że jest to jedna z najlepszych alternatyw dla szacowania niezawodności (Zinbarg et al.,, 2005, 2006; Revelle i Zinbarg, 2009), choć do tej pory jego funkcjonowanie w Warunkach skośności jest nieznane.
gdy istnieje korelacja między błędami lub istnieje więcej niż jeden ukryty wymiar w danych, wkład każdego wymiaru do całkowitej wariancji wyjaśnionej jest szacowany, uzyskując tak zwany hierarchiczny ω (WH), który pozwala nam skorygować najgorsze odchylenie przeszacowania α z danymi wielowymiarowymi (patrz Tarkkonen and Vehkalahti, 2005; Zinbarg et al., 2005; Revelle i Zinbarg, 2009)., Współczynniki wh i wt są równoważne w danych jednowymiarowych, więc będziemy odnosić się do tego współczynnika po prostu jako ω.
Greatest Lower Bound (GLB)
Sijtsma (2009) pokazuje w serii badań, że jednym z najpotężniejszych estymatorów niezawodności jest GLB—wydedukowany przez Woodhouse ' a i Jacksona (1977) z założeń klasycznej teorii testów (Cx = Ct + Ce)—macierz kowariancji między obiektami dla obserwowanych wyników punktowych Cx. To rozbija się na dwie części: suma między-element macierzy kowariancji dla pozycji true scores Ct; i między-element błąd kowariancji macierzy Ce (ten Berge and Sočan, 2004)., Jego wyrażenie to:
gdzie σx2 jest wariancją testową, A tr (Ce) odnosi się do śladu macierzy kowariancji błędu między elementami, która okazała się tak trudna do oszacowania. Jednym z rozwiązań było zastosowanie procedur czynnikowych, takich jak analiza minimalnego współczynnika Rang (procedura znana jako glb.fa). Niedawno procedura GLB algebraic (GLBa) została opracowana na podstawie algorytmu opracowanego przez Andreasa Moltnera (Moltner and Revelle, 2015)., Według Revelle ' a (2015a) procedura ta przyjmuje formę najbardziej wierną pierwotnej definicji Jacksona i Agunwamby (1977) i ma dodatkową zaletę wprowadzenia wektora do ważenia przedmiotów według znaczenia (Al-Homidan, 2008).
pomimo swoich teoretycznych zalet, GLB jest bardzo mało stosowany, chociaż niektóre ostatnie badania empiryczne wykazały, że współczynnik ten daje lepsze wyniki niż α (Lila et al., 2014) oraz α i ω (Wilcox et al., 2014)., Niemniej jednak, w małych próbkach, przy założeniu normalności, ma tendencję do zawyżania rzeczywistej wartości niezawodności (Shapiro and ten Berge, 2000); jednak jego funkcjonowanie w Warunkach nienormalnych pozostaje nieznane, szczególnie gdy rozkłady elementów są asymetryczne.
biorąc pod uwagę współczynniki zdefiniowane powyżej, a także uprzedzenia i ograniczenia każdego z nich, celem niniejszej pracy jest ocena wytrzymałości tych współczynników w obecności elementów asymetrycznych, biorąc również pod uwagę założenie równoważności tau i wielkość próby.,
metody
generowanie danych
dane zostały wygenerowane za pomocą oprogramowania R (R Development Core Team, 2013) i RStudio (Racine, 2012), zgodnie z modelem czynnikowym:
gdzie xij jest symulowaną odpowiedzią podmiotu i w pozycji J, λjk jest obciążeniem elementu j we współczynniku K (który został wygenerowany przez model jednofaktyczny); FK jest czynnikiem utajonym generowanym przez znormalizowany rozkład normalny (Średnia 0 i wariancja 1), A ej jest losowym błędem pomiaru każdego elementu również po znormalizowanym rozkładzie normalnym.,
Elementy Przekrzywione: Standardowe normalne Xij zostały przekształcone w celu wygenerowania rozkładów innych niż normalne przy użyciu procedury zaproponowanej przez Headricka (2002) przy zastosowaniu przekształceń wielomianu piątego rzędu:
Warunki Symulowane
aby ocenić wydajność współczynniki niezawodności (α, ω, Glb i GLBA) pracowaliśmy z trzema wielkościami próbek (250, 500, 1000), dwoma wielkościami testów: krótkim (6 pozycji) i długim (12 pozycji), dwoma warunkami równoważności Tau (jeden z równoważnością Tau i jeden bez, tj.,, congenic) i stopniowe włączanie elementów asymetrycznych (od wszystkich elementów normalnych do wszystkich elementów asymetrycznych). W krótkim teście niezawodność została ustalona na 0,731, co w obecności równoważności tau uzyskuje się z sześcioma elementami o obciążeniu czynnikowym = 0,558; natomiast model kongeneryczny otrzymuje się przez ustawienie obciążenia czynnikowego na wartości 0.3, 0.4, 0.5, 0.6, 0.7, i 0,8 (patrz dodatek i). W długim teście 12 pozycji niezawodność została ustalona na 0.,845 przyjmując te same wartości, co w krótkim teście zarówno dla równoważności tau, jak i modelu kongenerycznego (w tym przypadku dla każdej wartości lambda były po dwie pozycje). W ten sposób symulowano 120 warunków z 1000 replik w każdym przypadku.
Analiza danych
główne analizy przeprowadzono przy użyciu pakietów Psych (Revelle, 2015b) i GPArotation (Bernaards and Jennrich, 2015), które umożliwiają oszacowanie α i ω. Do szacowania GLB wykorzystano dwa skomputeryzowane podejścia: glb. fa (Revelle, 2015a) i glb.,algebraic (Moltner and Revelle, 2015), ten ostatni pracował przez autorów takich jak Hunt and Bentler (2015).
aby ocenić dokładność różnych estymatorów w odzyskiwaniu niezawodności, obliczyliśmy średni kwadrat błędu (Rmse) i bias. Pierwsza jest średnią z różnic między szacowaną i symulowaną niezawodnością i jest sformalizowana jako:
gdzie ρ^ jest szacowaną niezawodnością dla każdego współczynnika, ρ symulowaną niezawodnością i Nr liczbą replik., Odchylenie procentowe jest rozumiane jako różnica między średnią szacowanej niezawodności a symulowanej niezawodności i jest zdefiniowane jako:
w obu indeksach, im większa wartość, tym większa niedokładność estymatora, ale w przeciwieństwie do RMSE, odchylenie może być dodatnie lub ujemne; w tym przypadku można uzyskać dodatkowe informacje, czy współczynnik jest niedoszacowany lub zawyżony parametr symulowanej niezawodności., Zgodnie z zaleceniem Hoogland i Boomsma (1998) wartości RMSE < 0.05 i odchylenie % < 5% uznano za dopuszczalne.
wyniki
główne wyniki można zobaczyć w tabeli 1 (6 pozycji) i Tabeli 2 (12 pozycji). Te pokazują rmse i % bias współczynników w Tau-równoważności i kongenerycznych warunkach, i jak skośność rozkładu badania wzrasta wraz ze stopniowym włączaniem elementów asymetrycznych.
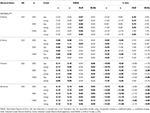
Tabela 1., RMSE i Bias z Tau-równoważności i congenic warunek dla 6 elementów, trzy wielkości próbki i liczby wypaczonych elementów.
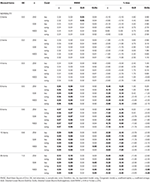
Tabela 2. RMSE i Bias z Tau-równoważności i congenic warunek dla 12 elementów, trzy wielkości próbki i liczby wypaczonych elementów.
tylko w Warunkach równoważności tau i normalności (skośność < 0.2) obserwuje się, że współczynnik α prawidłowo ocenia symulowaną niezawodność, podobnie jak ω., W stanie wrodzonym ω koryguje niedoszacowanie α. Zarówno GLB, jak i GLBa wykazują dodatnie odchylenie w normalności, jednak GLBa wykazuje około ½ mniej procent odchylenia niż GLB (patrz Tabela 1). Jeśli weźmiemy pod uwagę wielkość próbki, zauważymy, że wraz ze wzrostem wielkości testu dodatnie odchylenie GLB i GLBa maleje, ale nigdy nie znika.
w Warunkach asymetrycznych widzimy w tabeli 1, że zarówno α, jak i ω prezentują niedopuszczalną wydajność z rosnącym RMSE i niedoszacowaniem, które mogą osiągnąć bias> 13% dla współczynnika α (od 1 do 2% niższe dla ω)., Współczynniki GLB i GLBa przedstawiają niższy RMSE, gdy zwiększa się skośność testu lub liczba elementów asymetrycznych (patrz tabele 1, 2). Współczynnik GLB przedstawia lepsze szacunki, gdy wartość skośności testu wynosi około 0,30; GLBa jest bardzo podobny, prezentując lepsze szacunki niż ω z wartością skośności testu około 0,20 lub 0,30. Jednak gdy wartość skośności wzrasta do 0,50 lub 0,60, GLB prezentuje lepszą wydajność niż GLBa. Wielkość badania (6 lub 12 ítems) ma znacznie ważniejszy wpływ niż wielkość próbki na dokładność szacunków.,
dyskusja
w tym badaniu manipulowano czterema czynnikami: równoważnością tau lub modelem kongenerycznym, wielkością próby (250, 500 i 1000), liczbą pozycji testowych (6 i 12) oraz liczbą pozycji asymetrycznych (od 0 pozycji asymetrycznych do wszystkich pozycji asymetrycznych) w celu oceny odporności na obecność danych asymetrycznych w czterech analizowanych współczynnikach niezawodności. Wyniki te omówiono poniżej.,
w Warunkach równoważności Tau współczynniki α i ω są zbieżne, jednak przy braku równoważności tau (kongenerycznej) ω zawsze prezentuje lepsze oszacowania i mniejsze odchylenie RMSE i % niż α. W tym bardziej realistycznym stanie zatem (Green and Yang, 2009a; Yang and Green, 2011), α staje się negatywnie tendencyjnym estymatorem niezawodności (Graham, 2006; Sijtsma, 2009; Cho and Kim, 2015), a ω jest zawsze korzystniejszy od α (Dunn et al., 2014). W przypadku nieprzestrzegania założeń normalności ω jest najlepszym estymatorem wszystkich ocenianych współczynników (Revelle i Zinbarg, 2009).,
przechodząc do wielkości próby, zauważamy, że czynnik ten ma niewielki wpływ w normalności lub nieznaczne odejście od normalności: RMSE i bias maleją wraz ze wzrostem wielkości próby. Niemniej jednak, można powiedzieć, że dla tych dwóch współczynników, o wielkości próby 250 i normalności otrzymujemy stosunkowo dokładne szacunki(Tang and Cui, 2012; Javali et al., 2011)., W przypadku współczynników GLB i GLBa, ponieważ wielkość próby zwiększa RMSE, a odchylenie ma tendencję do zmniejszania się; jednak utrzymują one pozytywny odchylenie dla warunku normalności nawet przy dużych rozmiarach próby 1000 (Shapiro and ten Berge, 2000; ten Berge and Sočan, 2004; Sijtsma, 2009).
dla wielkości testu zazwyczaj obserwujemy wyższy rmse i bias z 6 pozycji niż z 12, co sugeruje, że im większa liczba pozycji, tym niższy rmse i bias estymatorów (Cortina, 1993). Ogólnie rzecz biorąc, trend jest utrzymywany zarówno dla 6, jak i 12 pozycji.,
kiedy patrzymy na efekt stopniowego włączania elementów asymetrycznych do zbioru danych, obserwujemy, że współczynnik α jest bardzo wrażliwy na elementy asymetryczne; wyniki te są podobne do tych znalezionych przez Sheng and Sheng (2012) i Green and Yang (2009b). Współczynnik ω wykazuje podobne wartości RMSE i bias do wartości α, ale nieco lepsze, nawet przy równoważności tau. Stwierdzono, że GLB i GLBa prezentują lepsze szacunki, gdy nachylenie testu odbiega od wartości bliskich 0.
biorąc pod uwagę, że w praktyce powszechne jest znajdowanie asymetrycznych danych (Micceri, 1989; Norton et al.,, 2013; Ho and Yu, 2014), sugestia Sijtsma (2009) dotycząca stosowania GLB jako estymatora niezawodności wydaje się uzasadniona. Inni autorzy, jak Revelle and Zinbarg (2009) i Green and Yang (2009a), zalecają stosowanie ω, jednak współczynnik ten dawał dobre wyniki tylko w stanie normalności, lub przy niskim udziale elementów skośnych. W każdym razie współczynniki te prezentowały większą przewagę teoretyczną i empiryczną niż α. Niemniej jednak zalecamy badaczom studiowanie nie tylko punktualnych szacunków, ale także wykorzystanie szacowania interwałowego (Dunn et al., 2014).,
wyniki te są ograniczone do warunków symulowanych i zakłada się, że nie ma korelacji między błędami. Wymagałoby to przeprowadzenia dalszych badań w celu oceny funkcjonowania różnych współczynników niezawodności przy bardziej złożonych strukturach wielowymiarowych (Reise, 2012; Green and Yang, 2015) oraz w obecności danych porządkowych i/lub kategorycznych, w których niezgodność z założeniem normalności jest normą.
podsumowanie
gdy suma wyników testu jest normalnie rozłożona (tj.,, wszystkie pozycje są normalnie rozłożone) ω powinny być pierwszym wyborem, a następnie α, ponieważ unikają problemów z przeszacowaniem prezentowanych przez GLB. Jednak, gdy jest niski lub umiarkowany test skośność GLBa należy stosować. GLB jest zalecane, gdy udział elementów asymetrycznych jest wysoki, ponieważ w tych warunkach nie zaleca się stosowania zarówno α, jak i ω jako estymatorów niezawodności, niezależnie od wielkości próby.
wkład autora
Rozwój idei badań i ram teoretycznych (IT, JA). Budowa RAM metodologicznych (IT, JA)., Rozwój składni języka R (IT, JA). Analiza i interpretacja danych (IT, JA). Omówienie wyników w świetle aktualnego tła teoretycznego (JA, IT). Przygotowanie i napisanie artykułu (JA, IT). Ogólnie rzecz biorąc, obaj autorzy w równym stopniu przyczynili się do rozwoju tej pracy.,
finansowanie
pierwszy autor ujawnił otrzymanie następującego wsparcia finansowego dla badań, autorstwo, i / lub publikacji tego artykułu: otrzymał wsparcie finansowe z chilijskiej Narodowej Komisji Badań Naukowych i technologicznych (CONICYT)” Becas Chile ” Program Stypendialny Doctoral (Grant no: 72140548).
Oświadczenie o konflikcie interesów
autorzy oświadczają, że badanie zostało przeprowadzone w przypadku braku jakichkolwiek relacji handlowych lub finansowych, które mogłyby być interpretowane jako potencjalny konflikt interesów.
, Współczynnik alfa i wewnętrzna struktura badań. Psychometrika 16, 297-334 doi: 10.1007/BF02310555
CrossRef Full Text/Google Scholar
McDonald, R. (1999). Teoria testu: jednolite leczenie. Mahwah, NJ: Lawrence Erlbaum Associates.
Google Scholar
r Development Core Team (2013). R: język i środowisko dla obliczeń statystycznych. Vienna: R Foundation for Statistical Computing.
Raykov, T. (1997)., Scale reliability, cronbach”s coefficient alpha, and violations of essential tau- equivalence with fixed congeneric components. Multivariate Behav. Res. 32, 329–353. doi: 10.1207/s15327906mbr3204_2
PubMed Abstract | CrossRef Full Text | Google Scholar
Raykov, T. (2001). Bias of coefficient alpha for fixed congeneric measures with correlated errors. Appl. Psychol. Meas. 25, 69–76. doi: 10.1177/01466216010251005
CrossRef Full Text | Google Scholar
Revelle, W. (2015b). Package „psych.,”Dostępny online pod adresem: http://org/r/psych-manual.pdf
Asymptotyczne odchylenie minimalnej analizy czynnika śladowego, z zastosowaniami do największej dolnej granicy niezawodności. Psychometrika 65, 413-425 doi: 10.1007/BF02296154
CrossRef Full Text/Google Scholar
ten Berge, J. M. F., And Sočan, G. (2004). Największe obniżenie wiąże się z wiarygodnością testu i hipotezą jednowymiarowości. Psychometrika 69, 613-625 doi: 10.,1007 / BF02289858
CrossRef Full Text / Google Scholar
Dolna granica wiarygodności wyniku całkowitego W teście złożonym z niejednorodnych elementów: II: procedura wyszukiwania w celu zlokalizowania największej dolnej granicy. Psychometrika 42, 579-591 doi: 10.1007/BF02295980
CrossRef Full Text/Google Scholar
dodatek I
składnia R do szacowania współczynników niezawodności z macierzy korelacji Pearsona., Wartości korelacji poza przekątną oblicza się mnożąc obciążenie współczynników elementów: (1) Model równoważny tau wszystkie są równe 0,3114 (λiλj = 0,558 × 0,558 = 0,3114) i (2) Model kompleksowy różnią się jako funkcja różnych obciążeń współczynników (np. element macierzy A1, 2 = λ1λ2 = 0,3 × 0,4 = 0,12). W obu przykładach prawdziwa niezawodność wynosi 0,731.
> omega(Cr,1)$alpha # 0.731
>omega (Cr,1)$omega.tot # współczynnik ω ogółem
0.,731
> glb.fa(Cr)$glb # GLB factorial procedure
0.731
> glb.algebraic(Cr)$glb # GLB algebraic procedure
0.731
> omega(Cr,1)$alpha # standardized Cronbach”s α
0.717
> omega(Cr,1)$omega.tot # coefficient ω total
0.731
> glb.fa(Cr)$glb # GLB factorial procedure
0.754
> glb.algebraic(Cr)$glb # GLB algebraic procedure
0.731