Model zagrożeń proporcjonalnych Coxa

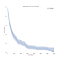
na osi x mamy czas w dniach. Na osi y mamy (Estymator) procent (technicznie, proporcja) osób w populacji, które „przetrwały” do tego czasu. Przetrwanie może być przenośne lub dosłowne., Może to być to, czy ludzie żyją do pewnego wieku, czy maszyna sprawia, że pewien czas bez awarii, lub może to być, czy ktoś pozostaje bezrobotny pewien czas po utracie pracy.

Mogą nadal żyć, maszyna może nadal działać lub ktoś może nadal być bezrobotny w momencie gromadzenia danych., Takie spostrzeżenia nazywane są „prawocenzurowanymi”, a radzenie sobie z cenzurą oznacza, że analiza przetrwania wymaga różnych narzędzi statystycznych.

funkcję survivor oznaczamy jako s, funkcję czasu. Jego wynikiem jest odsetek osób, które przeżyły w czasie t. (ponownie, technicznie jest to proporcja między 0 a 1, ale użyję tych dwóch słów zamiennie). Dla uproszczenia przyjmiemy techniczne założenie, że jeśli poczekamy wystarczająco długo, wszyscy testerzy ” umrą.”

będziemy indeksować tematy z indeksem dolnym, takim jak i lub j., Czas awarii całej populacji będzie oznaczony podobnym indeksem w zmiennej czasu t.

kolejną subtelnością do rozważenia jest to, czy traktujemy czas jako dyskretny (powiedzmy tydzień po tygodniu) czy ciągły. Filozoficznie rzecz biorąc, mierzymy czas tylko w dyskretnych przyrostach (powiedzmy do najbliższej sekundy)., Zwykle nasze dane mówią nam tylko, czy ktoś zmarł w danym roku lub czy maszyna zawiodła w danym dniu. Będę poruszał się tam iz powrotem między dyskretnymi i ciągłymi przypadkami w interesie utrzymania ekspozycji tak jasnej, jak to możliwe.

kiedy próbujemy modelować wpływ kowariantnych (np. wiek, płeć, rasa, producent maszyn), zazwyczaj będziemy zainteresowani zrozumieniem wpływu kowariantnej na wskaźnik zagrożenia. Współczynnik ryzyka to chwilowe prawdopodobieństwo niepowodzenia / śmierci / przejścia stanu w danym czasie t, uzależnione od tego, czy już przetrwało tak długo., Oznaczmy ją λ (t). Traktowanie czasu jako dyskretnego:

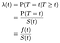
gdzie f jest ogólną gęstością prawdopodobieństwa niepowodzenia w czasie T. możemy ujednolicić dyskretne i ciągłe przypadki, dopuszczając funkcje Delta w „funkcji gęstości prawdopodobieństwa”. Zatem wynik λ = f / S jest taki sam dla przypadku ciągłego.

poprawimy przykład., Rozważmy Kontekst badania klinicznego, w którym lek początkowo powoduje, że choroba przechodzi w remisję. Powiemy, że lek „zawodzi” dla podmiotu, gdy choroba zaczyna się rozwijać dla podmiotu. Na koniec Załóżmy, że stany chorobowe badanych są mierzone co tydzień. Następnie, jeśli λ(3) = 0,1, oznacza to, że istnieje 10% szansa, że dla danego pacjenta, jeśli nadal jest w remisji przed 3. tygodniem, ich choroba zacznie się rozwijać w 3. tygodniu. Pozostałe 90% pozostanie w remisji.,

następnie ogólna funkcja gęstości prawdopodobieństwa f jest Tylko pochodną S w odniesieniu do czasu. (Ponownie, jeśli czas jest dyskretny, f jest tylko sumą niektórych funkcji delta).,341fa8b2″>

oznacza to, że jeśli znamy funkcję zagrożenia, możemy rozwiązać to równanie różniczkowe dla S:

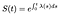
Jeśli czas jest dyskretny, to Całka sumy funkcji Delta zamienia się w sumę zagrożeń w każdym czasie dyskretnym.,

ok, to podsumowuje notację i podstawowe pojęcia, które będziemy potrzebować. Przejdźmy do dyskusji o modelach.

modele Nie-, pół-i w pełni parametryczne

jak już wcześniej wspomniałem, zazwyczaj interesuje nas modelowanie współczynnika zagrożenia λ.

w modelu nieparametrycznym nie przyjmujemy założeń co do postaci funkcjonalnej λ. Krzywa Kaplana-Meiera jest w tym przypadku estymatorem maksymalnego prawdopodobieństwa. Minusem jest to, że utrudnia to modelowanie jakichkolwiek efektów kowariantnych. Jest to trochę jak za pomocą wykresu punktowego, aby zrozumieć efekt kowariancji., Niekoniecznie tak pomocny jak model w pełni parametryczny, jak regresja liniowa.

w modelu w pełni parametrycznym Zakładamy dokładną postać funkcjonalną λ. Omówienie modeli w pełni parametrycznych jest sam w sobie pełnym artykułem, ale warto przeprowadzić bardzo krótką dyskusję. Poniższa tabela przedstawia trzy najpopularniejsze modele w pełni parametryczne. Każdy jest uogólniony przez następny, przechodząc od 1 do 2 do 3 parametrów. Forma funkcjonalna funkcji zagrożenia przedstawiona jest w kolumnie Środkowej. Logarytm funkcji zagrożenia jest również pokazany w ostatniej kolumnie., Przyjmuje się, że wszystkie parametry (ɣ, α, μ) są dodatnie, z wyjątkiem tego, że μ może być równe 0 w uogólnionym rozkładzie Weibulla (odwzorowaniu rozkładu Weibulla).

patrząc na logarytm pokazuje nam, że model wykładniczy zakłada, że funkcja zagrożenia jest stała. Model Weibulla zakłada, że wzrasta, jeśli α>1, stała, jeśli α=1, i maleje, jeśli α<1., Uogólniony model Weibulla zaczyna się tak samo jak model Weibulla (na początku ln s = 0). Potem pojawia się dodatkowy termin μ.

problem z tymi modelami polega na tym, że składają silne założenia dotyczące danych. W pewnych kontekstach mogą istnieć powody, aby sądzić, że te modele dobrze pasują. Ale z tymi i kilkoma innymi dostępnymi opcjami istnieje duże ryzyko wyciągnięcia nieprawidłowych wniosków z powodu niedoprecyzowania modelu.

dlatego tak popularny jest model Półparametryczny Coxa., Nie przyjmuje się żadnych założeń funkcjonalnych dotyczących kształtu funkcji zagrożenia; zamiast tego przyjmuje się założenia funkcjonalno-formalne dotyczące skutków samych kowariantnych.,

Model zagrożeń proporcjonalnych Cox

model zagrożeń proporcjonalnych Cox jest zwykle podany w kategoriach czasu t, wektora kowariantnego x i wektora współczynnika β jako

gdzie λₒ jest arbitralną funkcją czasu, zagrożenie wyjściowe. Iloczyn punktowy X i β przyjmuje się w wykładniku, podobnie jak w standardowej regresji liniowej., Niezależnie od wartości współzmiennych, wszyscy badani mają takie samo początkowe zagrożenie λₒ. Następnie dokonuje się korekt w oparciu o kowarianty.

interpretacja wyników

załóżmy dla minuty, że dopasowaliśmy Model zagrożeń proporcjonalnych Coxa do naszych danych, który składał się z

1. kolumny określającej czas dla każdego podmiotu
2. kolumny określającej, czy podmiot był „obserwowany” (aby nie powiódł się lub, w naszym preferowanym przykładzie, aby nastąpił postęp choroby). Wartość 1 oznacza, że podmiot miał postęp choroby., Wartość 0 oznacza, że w czasie ostatniej obserwacji choroba nie postępowała. Obserwacja została ocenzurowana.
3. kolumny dla naszych kowariantnych X.

po dopasowaniu otrzymamy wartości dla β. Na przykład, załóżmy dla uproszczenia, że istnieje jedna kowariantna. Wartość β=0,1 oznacza, że zwiększenie współzmienności o 1 prowadzi do około 10% wysokiego ryzyka progresji choroby w danym momencie., Dokładna wartość to

dla małych wartości β, sama wartość β jest całkiem dobrym przybliżeniem dokładnego wzrostu zagrożenia. Dla większych wartości β należy obliczyć dokładną ilość.

innym sposobem wyrażenia β=0,1 jest to, że wraz ze wzrostem x ryzyko wzrasta w tempie 10% na wzrost x o 1. Większa 10.,52% pochodzi z (ciągłego) compoundingu, podobnie jak w przypadku odsetek złożonych.

ponadto β = 0 oznacza brak efektu, a β ujemny oznacza, że ryzyko jest mniejsze wraz ze wzrostem współzmienności. Zauważ, że w przeciwieństwie do standardowych regresji, nie ma terminu przechwytywania. Zamiast tego intercept jest wchłaniany do wyjściowego zagrożenia λₒ, które można również oszacować(patrz poniżej).

wreszcie, zakładając, że oszacowaliśmy podstawową funkcję zagrożenia, możemy skonstruować funkcję przetrwania.,

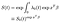
funkcja wyjściowa jest podniesiona do potęgi współczynnika EXP(xßß) pochodzącego z kowariantów. Należy zachować pewną ostrożność przy interpretacji podstawowej funkcji przetrwania, która z grubsza odgrywa rolę terminu przechwytywania w regularnej regresji liniowej. Jeśli kowarianty zostały wyśrodkowane (średnia 0), to reprezentuje funkcję survivor dla” przeciętnego ” podmiotu.,

Szacowanie proporcjonalnego modelu zagrożeń Coxa

w latach 70.XX wieku David Cox, brytyjski matematyk, zaproponował sposób oszacowania β bez konieczności szacowania podstawowego zagrożenia λₒ. Ponownie, zagrożenie wyjściowe można oszacować później. Jak wspomniano wcześniej, zobaczymy, że liczy się kolejność zaobserwowanych niepowodzeń, a nie same czasy.

przed przejściem do oceny warto omówić powiązania. Ponieważ zazwyczaj obserwujemy dane tylko w przyrostach dyskretnych, możliwe jest, że mogą wystąpić dwie awarie w tym samym czasie., Na przykład dwie maszyny mogą zawieść w tym samym tygodniu, a nagrywanie odbywa się tylko raz w tygodniu. Powiązania te sprawiają, że analiza sytuacji jest dość skomplikowana, nie dodając wiele wglądu. W związku z tym, będę czerpać szacunki w przypadku braku powiązań.

Przypomnijmy, że nasze dane składają się z obserwacji niektórych awarii liczbowych w czasie dyskretnym. Niech R (t) oznacza populację „zagrożoną” w czasie t. jeśli podmiot w naszym badaniu nie powiódł się (choroba postępuje, na przykład) przed czasem t, nie są „zagrożeni”.,”Ponadto, jeśli przedmiot naszego badania został ocenzurowany w czasie przed czasem t, również nie są” zagrożone.”

w zwykły sposób chcemy skonstruować funkcję prawdopodobieństwa (jakie jest prawdopodobieństwo, że zaobserwowalibyśmy dane, które zrobiliśmy, biorąc pod uwagę kowarianty i współczynniki), a następnie zoptymalizować ją, aby uzyskać Estymator maksymalnego prawdopodobieństwa.

dla każdego dyskretnego czasu, kiedy zaobserwowaliśmy błąd testera j, prawdopodobieństwo wystąpienia takiego błędu, biorąc pod uwagę, że wystąpił błąd, jest poniżej. Suma jest przejmowana przez wszystkie podmioty zagrożone w czasie j.,

(równanie 1) prawdopodobieństwo, że tester j zawiedzie w czasie J zamiast innego testera

zauważ, że podstawowe zagrożenie λₒ wypadło! Bardzo wygodne. Z tego powodu prawdopodobieństwo, które konstruujemy, jest tylko częściowym prawdopodobieństwem. Zauważ również, że czasy w ogóle się nie pojawiają., Termin dla podmiotu j zależy tylko od tego, który podmiot nadal żyje w czasie j, co z kolei zależy tylko od kolejności, w jakiej testerzy są ocenzurowani lub Obserwowani jako nieudacznicy.

prawdopodobieństwo częściowe jest oczywiście tylko iloczynem tych terminów, po jednym za każdą zaobserwowaną porażkę (brak terminów dla ocenzurowanych obserwacji).,

prawdopodobieństwo częściowe loga jest wtedy

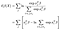
dopasowanie odbywa się za pomocą standardowych metod numerycznych, na przykład w pakiecie Pythona statsmodels, a macierz wariancja-KOWARIANCJA dla estymacji jest podana przez (odwrotność) macierz informacji Fishera. Nic ciekawego.,

Szacowanie podstawowej funkcji przetrwania

teraz, gdy oszacowaliśmy współczynniki, możemy oszacować funkcję przetrwania. Jest to bardzo podobne do oszacowania krzywej Kaplana-Meiera.

postulujemy terminy α indeksowane przez i. w czasie i, wyjściowa krzywa przeżycia powinna zmniejszyć się o ułamek α reprezentujący odsetek osób zagrożonych niepowodzeniem w czasie i., Innymi słowy

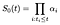
aby obliczyć maksymalny Estymator prawdopodobieństwa dla α, rozważamy wkład prawdopodobieństwa z podmiotu i, który nie powiedzie się w czasie I i oddzielnie wkład z tych, które są ocenzurowane w czasie i.

dla podmiotu, który nie powiedzie się w czasie i, prawdopodobieństwo jest podane przez prawdopodobieństwo, że żyją w czasie i, mniejsze prawdopodobieństwo, że żyją w następnym czasie i+1. (Tymczasowo Zakładamy, że czasy są uporządkowane).,

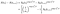
jeśli zamiast tego są one cenzurowane w czasie i, wkład jest tylko prawdopodobieństwo, że żyją w czasie po i, tzn. że jeszcze nie umarli., To jest po prostu

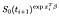
obserwacja

istnieje dodatkowy termin od obserwowanych obiektów(tzn. Obserwowani nie są ocenzurowani)., Prawdopodobieństwo logowania staje się

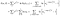
byłem trochę niechlujny, jeśli chodzi o śledzenie punktów końcowych (i Vs.i+1), ale wszystko się uda.

są tylko terminy, które uznaliśmy za nieudane., Różnicując w odniesieniu do α-j i zakładając brak powiązań, otrzymujemy wkład z sumy po lewej tylko dla podmiotów żyjących w czasie j, a pojedynczy wkład z terminu po prawej.,kwal do 0 oznacza, że możemy uzyskać maksymalne oszacowanie prawdopodobieństwa dla α, używając naszych oszacowań dla β jako rozwiązania kilku równań, po jednym dla każdego obiektu, który został zaobserwowany jako nieudany:

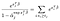
rozszerzenia i zastrzeżenia

jest wiele więcej do powiedzenia na temat modeli proporcjonalnych zagrożeń Coxa, ale postaram się krótko i po prostu wspomnieć o kilku rzeczach.,

na przykład można rozważyć regresory zmieniające się w czasie i jest to możliwe.

inną kluczową rzeczą, o której należy pamiętać, jest pominięcie zmiennej bias. W standardowej regresji liniowej pominięte zmienne nieskorelowane z regresorami nie są dużym problemem. Nie jest to prawdą w analizie przeżycia. Załóżmy, że w naszych danych mamy dwie równe wielkości i zbadane subpopulacje, każda ze stałym wskaźnikiem zagrożenia, jedna wynosi 0,1, a druga 0,5. Początkowo zobaczymy wysoki wskaźnik zagrożenia(średnia, zaledwie 0,3)., W miarę upływu czasu populacja z wysokim wskaźnikiem zagrożenia opuści populację, a my zaobserwujemy wskaźnik zagrożenia, który spada w kierunku 0,1. Jeśli pominiemy zmienną reprezentującą te dwie populacje, nasz podstawowy wskaźnik zagrożenia będzie pomieszany.