definicje statystyk> Anova
spis treści:
- Test Anova
- One way ANOVA
- two way ANOVA
- co to jest Manova?
- co to jest Anova?
- Jak uruchomić Test ANOVA
- Anova vs. T
- powtarzane miary ANOVA
- sferyczność
Test ANOVA
Co to jest test ANOVA?, Obejrzyj film wprowadzający lub przeczytaj poniżej:
nadal masz problemy? Chegg.com dopasuje Cię do korepetytora (pierwsza lekcja jest darmowa!).
test ANOVA to sposób na sprawdzenie, czy wyniki ankiety lub eksperymentu są znaczące. Innymi słowy, pomagają dowiedzieć się, czy trzeba odrzucić hipotezę zerową lub zaakceptować alternatywną hipotezę.
zasadniczo testujesz grupy, aby sprawdzić, czy jest między nimi różnica., Przykłady, kiedy możesz chcieć przetestować różne grupy:
- grupa pacjentów psychiatrycznych próbuje trzech różnych terapii: poradnictwa, leków i biofeedbacku. Chcesz sprawdzić, czy jedna terapia jest lepsza od innych.
- producent ma dwa różne procesy wytwarzania żarówek. Chcą wiedzieć, czy jeden Proces jest lepszy od drugiego.
- uczniowie z różnych uczelni przystępują do tego samego egzaminu. Chcesz sprawdzić, czy jeden college jest lepszy od drugiego.
co oznacza „jednokierunkowy” lub „dwukierunkowy?,
jednokierunkowa lub dwukierunkowa odnosi się do liczby zmiennych niezależnych (IVs) w analizie testu wariancji.
- jednokierunkowa ma jedną zmienną niezależną(z 2 poziomami). Na przykład: brand of cereal,
- dwukierunkowa ma dwie niezależne zmienne (może mieć wiele poziomów). Na przykład: mamba, związek / randka
czym są „grupy” lub „poziomy”?
grupy lub poziomy są różnymi grupami w ramach tej samej zmiennej niezależnej. W powyższym przykładzie twoje poziomy dla „marki zbóż” mogą być Lucky Charms, otręby z rodzynkami, płatki kukurydziane — łącznie trzy poziomy., Twoje poziomy „kalorii” mogą być: słodzone, niesłodzone — w sumie dwa poziomy.
Załóżmy, że studiujesz, czy połączenie grupy wsparcia alkoholowego i indywidualnego poradnictwa jest najskuteczniejszym sposobem na obniżenie spożycia alkoholu. Możesz podzielić uczestników badania na trzy grupy lub poziomy:
- tylko leki,
- leki i doradztwo,
- tylko doradztwo.
zmienną zależną będzie liczba spożywanych napojów alkoholowych dziennie.,
Jeśli Twoje grupy lub poziomy mają strukturę hierarchiczną( każdy poziom ma unikalne podgrupy), użyj zagnieżdżonej ANOVA do analizy.
co oznacza „replikacja”?
chodzi o to, czy replikujesz(tzn. powielasz) test (y) z wieloma grupami. W przypadku dwukierunkowej ANOVA z replikacją, masz dwie grupy, a osoby w tej grupie robią więcej niż jedną rzecz (tj. dwie grupy studentów z dwóch uczelni biorących udział w dwóch testach). Jeśli masz tylko jedną grupę wykonującą dwa testy, używasz ich bez replikacji.
rodzaje testów.,
istnieją dwa główne typy: jednokierunkowy i dwukierunkowy. Testy dwukierunkowe mogą być z replikacją lub bez niej.
- One-way ANOVA between groups: używany, gdy chcesz przetestować dwie grupy, aby sprawdzić, czy jest między nimi różnica.
- dwukierunkowa ANOVA bez replikacji: używana, gdy masz jedną grupę i dwukrotnie testujesz tę samą grupę. Na przykład, testujesz jedną grupę osób przed i po przyjęciu leku, aby sprawdzić, czy działa, czy nie.
- dwukierunkowa ANOVA z replikacją: dwie grupy, a członkowie tych grup robią więcej niż jedną rzecz., Na przykład dwie grupy pacjentów z różnych szpitali próbujących dwóch różnych terapii.
powrót do góry
jednokierunkowa ANOVA
jednokierunkowa ANOVA jest używana do porównywania dwóch środków z dwóch niezależnych (niepowiązanych) grup za pomocą rozkładu F. Hipoteza zerowa dla testu jest to, że dwa środki są równe. W związku z tym znaczący wynik oznacza, że oba środki są nierówne.
przykłady kiedy używać jednokierunkowej ANOVA
sytuacja 1: masz grupę osób losowo podzielonych na mniejsze grupy i wypełniających różne zadania., Na przykład możesz studiować wpływ herbaty na odchudzanie i tworzyć trzy grupy: zieloną herbatę, czarną herbatę i brak herbaty.
sytuacja 2: podobna do sytuacji 1, ale w tym przypadku jednostki dzielą się na grupy na podstawie posiadanego atrybutu. Na przykład, możesz studiować siłę nóg ludzi w zależności od wagi. Możesz podzielić uczestników na kategorie wagowe (otyłość, nadwaga i normalna) i zmierzyć ich siłę nóg na maszynie wagowej.,
ograniczenia jednokierunkowej ANOVA
jednokierunkowa ANOVA powie Ci, że przynajmniej dwie grupy różniły się od siebie. Ale nie powie Ci, które grupy były różne. Jeśli twój test zwróci znaczącą statystykę f, być może będziesz musiał przeprowadzić test ad hoc (jak najmniej znaczący test różnicy), aby dokładnie określić, które grupy miały różnicę w środkach.
Powrót do góry
dwukierunkowa ANOVA
dwukierunkowa Anova jest rozszerzeniem jednokierunkowej ANOVA. W jeden sposób Masz jedną zmienną niezależną wpływającą na zmienną zależną., Z Anovą dwukierunkową, istnieją dwie niezależne. Użyj dwukierunkowej ANOVA, gdy masz jedną zmienną pomiarową (tj. zmienną ilościową) i dwie zmienne nominalne. Innymi słowy, jeśli Twój eksperyment ma ilościowy wynik i masz dwie kategoryczne zmienne wyjaśniające, odpowiednia jest dwukierunkowa ANOVA.
na przykład możesz dowiedzieć się, czy istnieje interakcja między dochodem a płcią dla poziomu lęku na rozmowach kwalifikacyjnych. Poziom lęku jest wynikiem, lub zmienna, która może być mierzona. Płeć i dochód to dwie zmienne kategoryczne., Te zmienne kategoryczne są również zmiennymi niezależnymi, które nazywane są czynnikami w dwojaki sposób ANOVA.
czynniki można podzielić na poziomy. W powyższym przykładzie poziom dochodów można podzielić na trzy poziomy: niski, średni i wysoki dochód. Płeć można podzielić na trzy poziomy: męski, żeński i transseksualny. Grupy terapeutyczne są wszystkie możliwe kombinacje czynników. W tym przykładzie byłoby 3 x 3 = 9 grup terapeutycznych.
efekt główny i efekt interakcji
wyniki z dwukierunkowej ANOVA obliczą efekt główny i efekt interakcji., Główny efekt jest podobny do jednokierunkowego ANOVA: efekt każdego czynnika jest rozpatrywany oddzielnie. Dzięki efektowi interakcji wszystkie czynniki są brane pod uwagę w tym samym czasie. Efekty interakcji między czynnikami są łatwiejsze do zbadania, jeśli w każdej komórce znajduje się więcej niż jedna obserwacja. W powyższym przykładzie można wprowadzić wiele wyników stresu do komórek. Jeśli wprowadzasz wiele obserwacji do komórek, liczba w każdej komórce musi być równa.
dwie hipotezy zerowe są testowane, jeśli umieszczasz jedną obserwację w każdej komórce., W tym przykładzie hipotezy te byłyby następujące:
H01: Wszystkie grupy dochodów mają jednakowy średni stres.
H02: Wszystkie grupy płci mają jednakowy średni stres.
w przypadku wielokrotnych obserwacji w komórkach testowałbyś również trzecią hipotezę:
H03: czynniki są niezależne lub efekt interakcji nie istnieje.
dla każdej testowanej hipotezy obliczana jest F-statystyka.
założenia dla Anova dwukierunkowego
- populacja musi być zbliżona do rozkładu normalnego.
- próbki muszą być niezależne.
- wariancje populacji muszą być równe.,
- grupy muszą mieć jednakowe rozmiary próbek.
powrót do góry
Co to jest MANOVA?
MANOVA jest tylko ANOVA z kilkoma zależnymi zmiennymi. Jest to podobne do wielu innych testów i eksperymentów w tym, że jego celem jest, aby dowiedzieć się, czy zmienna odpowiedzi (tj. zmienna zależna) zmienia się manipulując zmienną niezależną. Test pomaga odpowiedzieć na wiele pytań badawczych, m.in.:
- czy zmiany zmiennych niezależnych mają statystycznie istotny wpływ na zmienne zależne?
- jakie są interakcje między zmiennymi zależnymi?,
- jakie są interakcje między zmiennymi niezależnymi?
przykład MANOVA
Załóżmy, że chcesz dowiedzieć się, czy różnica w podręcznikach wpływa na wyniki uczniów z matematyki i nauk ścisłych. Ulepszenia w matematyce i nauce oznaczają, że istnieją dwie zmienne zależne, więc Manova jest odpowiednia.
Anova da ci pojedynczą (jednokrotną) wartość f, podczas gdy MANOVA da ci wielowymiarową wartość f. MANOVA testuje wiele zmiennych zależnych, tworząc nowe, sztuczne, zależne zmienne, które maksymalizują różnice grupowe., Te nowe zmienne zależne są liniowymi kombinacjami mierzonych zmiennych zależnych.
interpretacja wyników MANOVA
Jeśli wielowymiarowa wartość F wskazuje, że test jest statystycznie istotny, oznacza to, że coś jest istotne. W powyższym przykładzie nie wiadomo, czy wyniki z matematyki uległy poprawie, czy wyniki z nauk ścisłych (lub oba)., Gdy uzyskasz znaczący wynik, będziesz musiał przyjrzeć się poszczególnym komponentom (jednostkowym testom F), aby zobaczyć, które zmienne zależne przyczyniły się do statystycznie istotnego wyniku.
zalety i wady MANOVA vs.ANOVA
zalety
- MANOVA umożliwia testowanie wielu zmiennych zależnych.
- MANOVA może chronić przed błędami typu I.
wady
- MANOVA jest wielokrotnie bardziej skomplikowana niż ANOVA, co sprawia, że wyzwaniem jest sprawdzenie, które zmienne niezależne wpływają na zmienne zależne.,
- Po dodaniu każdej nowej zmiennej traci się jeden stopień swobody.
- zmienne zależne powinny być nieskorelowane w jak największym stopniu. Jeśli są one skorelowane, utrata stopni swobody oznacza, że nie ma wiele zalet w tym więcej niż jedną zmienną zależną od testu.
Reference:
(SFSU)
Back to Top
Co to jest Anova?
ANOVA czynnikowa jest analizą testu wariancji z więcej niż jedną zmienną niezależną, czyli „czynnikiem”. Może również odnosić się do więcej niż jednego poziomu zmiennej niezależnej., Na przykład eksperyment z grupą leczoną i grupą kontrolną ma jeden czynnik (leczenie), ale dwa poziomy (leczenie i kontrola). Terminy „dwudrożny” i „trójdrożny” odnoszą się do liczby czynników lub liczby poziomów w teście. Cztery drogi ANOVA i powyżej są rzadko stosowane, ponieważ wyniki testu są złożone i trudne do interpretacji.
- ANOVA dwukierunkowa ma dwa czynniki (zmienne niezależne) i jedną zmienną zależną. Na przykład czas spędzony na nauce i wcześniejsza wiedza to czynniki, które wpływają na to, jak dobrze wypadasz na teście.,
- ANOVA trójstronna ma trzy czynniki (zmienne niezależne) i jedną zmienną zależną. Na przykład czas spędzony na nauce, wcześniejsza wiedza i godziny snu to czynniki, które wpływają na to, jak dobrze wypadasz na teście
Anova jest skutecznym sposobem przeprowadzania testu. Zamiast wykonywania serii eksperymentów, w których testujesz jedną zmienną niezależną przeciwko jednej zmiennej zależnej, możesz przetestować wszystkie zmienne niezależne w tym samym czasie.
zmienność
w jednokierunkowej ANOVA zmienność wynika z różnic między grupami i różnic w obrębie grup., W czynnikowej ANOVA każdy poziom i czynnik są sparowane ze sobą („skrzyżowane”). Pomaga to zobaczyć, jakie interakcje dzieją się między poziomami i czynnikami. Jeśli istnieje interakcja, to różnice w jednym czynnikiem zależą od różnic w innym.
Załóżmy, że biegałeś w dwie strony, aby sprawdzić wyniki mężczyzn/kobiet na egzaminie końcowym. Badani mieli 4, 6 lub 8 godzin snu.,
- IV1: seks (Mężczyzna/Kobieta)
- IV2: SEN (4/6/8)
- DV: końcowy wynik egzaminu
dwukierunkowa ANOVA pomoże Ci odpowiedzieć na następujące pytania:
- czy seks jest głównym efektem? Innymi słowy, czy mężczyźni i kobiety różnią się znacząco pod względem wyników egzaminu?
- czy sen jest głównym efektem? Innymi słowy, czy osoby, które miały 4,6 lub 8 godzin snu, różnią się znacząco w swojej wydajności?
- czy istnieje istotna interakcja między czynnikami? Innymi słowy, jak godziny snu i seksu współdziałają z wynikami egzaminu?,
- czy na różnych poziomach snu można znaleźć jakieś różnice w wynikach seksualnych i egzaminacyjnych?
założenia normalności czynnikowej ANOVA
- : zmienna zależna jest rozkładana normalnie.
- niezależność: obserwacje i grupy są od siebie niezależne.
- równość wariancji: wariancje populacji są równe dla różnych czynników/poziomów.
jak uruchomić ANOVA
te testy są bardzo czasochłonne ręcznie. W prawie każdym przypadku będziesz chciał używać oprogramowania., Na przykład w programie Excel dostępnych jest kilka opcji:
- dwukierunkowa ANOVA w programie Excel z replikacją i bez replikacji.
- One way ANOVA w Excelu 2013.
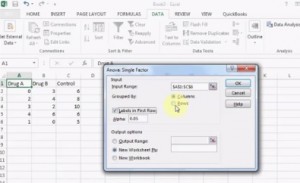
Uruchamianie testu w Excelu.
testy ANOVA w pakietach statystyk są uruchamiane na danych parametrycznych. Jeśli masz dane rangi lub uporządkowane, będziesz chciał uruchomić nieparametryczną ANOVA (Zwykle znajdującą się pod innym nagłówkiem w oprogramowaniu, takim jak „testy nieparametryczne”).,
kroki
jest mało prawdopodobne, że będziesz chciał wykonać ten test ręcznie, ale jeśli musisz, Są to kroki, które chcesz wykonać:
- Znajdź średnią dla każdej z grup.
- Znajdź średnią ogólną(średnią z grup połączonych).
- Znajdź zmienność wewnątrz grupy; całkowite odchylenie wyniku każdego członka od średniej grupy.
- Znajdź zmienność między grupami: odchylenie średniej dla każdej grupy od średniej ogólnej.
- Znajdź statystykę F: stosunek zmienności grupy do zmienności grupy.
ANOVA vs., Test T
Test T ucznia powie Ci, czy istnieje znaczna różnica między grupami. Test t porównuje środki, podczas gdy ANOVA porównuje różnice między populacjami.
możesz technicznie wykonać serię testów t na swoich danych. Jednak w miarę wzrostu liczby grup, możesz skończyć z wieloma porównaniami par, które musisz uruchomić. ANOVA da ci jedną liczbę (f-statystyka) i jedną wartość p, aby pomóc ci poprzeć lub odrzucić hipotezę zerową.,
Powrót do góry
powtarzane miary ANOVA
powtarzane miary ANOVA jest prawie taka sama jak jednokierunkowa ANOVA, z jedną główną różnicą: testujesz powiązane grupy, a nie niezależne. Nazywa się to powtarzanymi miarami, ponieważ ta sama grupa uczestników jest mierzona w kółko. Na przykład, można studiować poziom cholesterolu tej samej grupy pacjentów w 1, 3, i 6 miesięcy po zmianie diety. W tym przykładzie zmienną niezależną jest „czas” , a zmienną zależną jest ” cholesterol.,”Zmienną niezależną nazywa się zwykle czynnikiem wewnątrz-podmiotowym.
powtarzane miary ANOVA są podobne do prostej konstrukcji wielowymiarowej. W obu testach, ci sami uczestnicy są mierzone w kółko. Jednak przy powtarzanych pomiarach ta sama charakterystyka jest mierzona w innym stanie. Na przykład, ciśnienie krwi jest mierzona w stanie „Czas”. Dla prostej konstrukcji wielowymiarowej jest to cecha, która się zmienia. Na przykład można zmierzyć ciśnienie krwi, tętno i tempo oddychania w czasie.,
powody stosowania powtarzających się miar ANOVA
- gdy zbierasz dane od tych samych uczestników w danym okresie czasu, różnice indywidualne (źródło różnic między grupami) są zmniejszane lub eliminowane.
- testowanie jest bardziej wydajne, ponieważ wielkość próby nie jest podzielona między grupy.
- test może być ekonomiczny, ponieważ korzystasz z tych samych uczestników.,
założenia dla powtarzanych miar ANOVA
wyniki powtarzanych miar ANOVA będą ważne tylko wtedy, gdy następujące założenia nie zostały naruszone:
- musi istnieć jedna zmienna niezależna i jedna zmienna zależna.
- zmienna zależna musi być zmienną ciągłą, na skali przedziału lub skali stosunku.
- zmienna niezależna musi być kategoryczna, zarówno w skali nominalnej, jak i Porządkowej.
- idealnie, poziomy zależności między parami grup są równe („sferyczność”)., Poprawki są możliwe, jeśli to założenie zostanie naruszone.
powtarzane miary ANOVA w SPSS: kroki
Krok 1: Kliknij „Analizuj”, a następnie najedź kursorem na „ogólny model liniowy.”Kliknij” Powtarzane Miary.”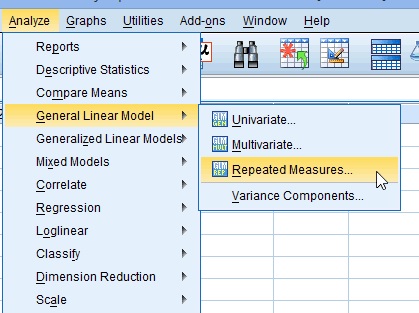
Krok 2: Zamień nazwę „factor1” na coś, co reprezentuje Twoją niezależną zmienną. Na przykład, można umieścić „wiek” lub ” czas.”
Krok 3: Wprowadź ” liczbę poziomów.”Tyle razy mierzono zmienną zależną. Na przykład, jeśli mierzysz co tydzień przez łącznie 4 tygodnie, liczba ta będzie wynosić 4.,
Krok 4: Kliknij przycisk” Dodaj”, a następnie nadaj nazwę zmiennej zależnej.
Krok 5: Kliknij przycisk „Dodaj”. Pojawi się okno definiujące powtarzające się miary. Kliknij przycisk „Definiuj”.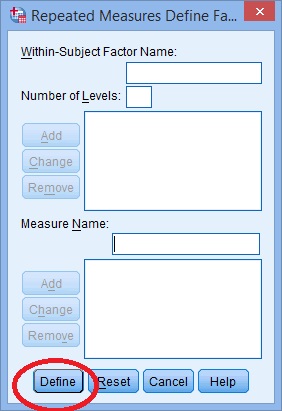
Krok 6: Użyj klawiszy strzałek, aby przenieść zmienne Z Lewej do prawej, aby ekran wyglądał podobnie do poniższego obrazu: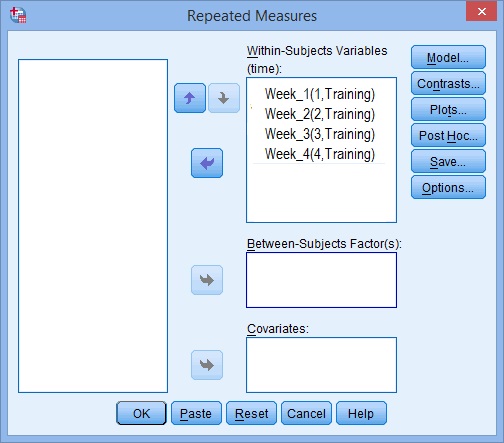
Krok 7: Kliknij „wykresy” i użyj klawiszy strzałek, aby przenieść czynnik z lewego pola na pole Osi Poziomej.
Krok 8: Kliknij „Dodaj”, a następnie kliknij” Kontynuuj ” u dołu okna.,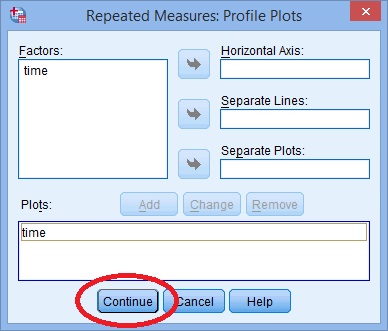
Krok 9: Kliknij „Opcje”, a następnie przenieś swoje czynniki z lewego pola do wyświetlacza oznacza dla pola po prawej stronie.
krok 10: Kliknij następujące pola wyboru:
- Porównaj główne efekty.
- statystyki opisowe.
- szacunki wielkości efektu.
krok 11: Wybierz „Bonferroni” z menu rozwijanego w sekcji Regulacja przedziału ufności.
krok 12: kliknij „Kontynuuj”, a następnie kliknij „OK”, aby uruchomić test.,
Back to Top
sferyczność
w statystyce sferyczność (ε) odnosi się do testu sferyczności Mauchly 'ego, który został opracowany w 1940 roku przez Johna W. Mauchly' ego, który współtworzył pierwszy komputer elektroniczny ogólnego przeznaczenia.
definicja
sferyczność jest stosowana jako założenie w miarach powtarzalnych. Założenie mówi, że wariancje różnic między wszystkimi możliwymi parami grupowymi są równe. Jeśli Twoje dane naruszają to założenie, może to spowodować wzrost błędu typu I (niepoprawne odrzucenie hipotezy zerowej).,
bardzo często powtarzające się środki ANOVA powodują naruszenie założenia. Jeśli założenie zostało naruszone, opracowano poprawki, które mogą uniknąć wzrostu poziomu błędu typu I. Korekcję stosuje się do stopni swobody w rozkładzie F.
Test sferyczności Mauchly 'ego
test sferyczności Mauchly' ego może być uruchamiany w większości programów statystycznych, gdzie zwykle jest domyślnym testem sferyczności. Test Mauchly ' ego jest idealny dla próbek średniej wielkości., Może nie wykryć sferyczności w małych próbkach i może nadmiernie wykryć w dużych próbkach.
Jeśli test zwróci małą wartość p (p ≤.05), jest to wskazanie, że Twoje dane naruszyły założenie. Poniższy obraz wyników SPSS dla ANOVA pokazuje, że znaczenie” sig ” dołączone do Mauchly jest .274. Oznacza to, że założenie nie zostało naruszone dla tego zestawu danych.
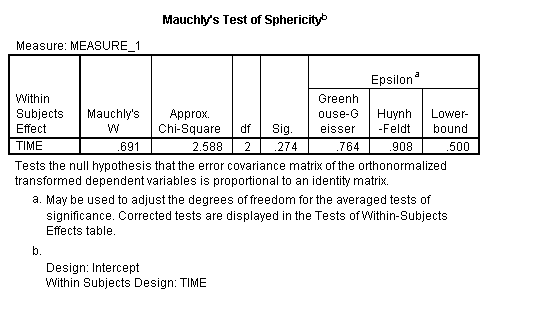
Obraz: uvm.,EDU
opisałbyś powyższy wynik jako „Test Mauchly' ego wykazał, że założenie sferyczności nie zostało naruszone, 274.”
Jeśli twój test zwrócił małą wartość p, powinieneś zastosować korektę, Zwykle:
- greehouse-GEISSER correction.
- korekta Huynh-Feldt.
gdy ε ≤ 0,75( lub nie wiesz, jaka jest wartość dla statystyki), użyj korekty Greenhouse-Geisser.
gdy > .75, użyj korekcji Huynh-Feldt.,
powrót do góry
Wielka średnia
ANOVA vs regresja
——————————————————————————
potrzebujesz pomocy w zadaniu domowym lub pytaniu testowym? Dzięki badaniu Chegg możesz uzyskać krok po kroku rozwiązania swoich pytań od eksperta w tej dziedzinie. Twoje pierwsze 30 minut z korepetytorem Chegg jest bezpłatne!