
Pitagorasa
ponad 2000 lat temu było niesamowite odkrycie o trójkątach:
gdy trójkąt ma kąt prosty (90°) …
… i kwadraty są wykonane na każdym ztrzy strony, …
… wtedy największy kwadrat ma dokładnie ten sam obszar, co dwa pozostałe kwadraty razem złożone!,
nazywa się to twierdzeniem Pitagorasa i może być zapisane w jednym krótkim równaniu:
a2 + b2 = c2
Uwaga:
- C jest najdłuższym bokiem trójkąta
- a i B są dwoma pozostałymi bokami
definicja
najdłuższy bok trójkąta nazywa się” przeciwprostokątną”, więc formalna definicja brzmi:
w trójkącie prostokąt:
kwadrat trójkąta jest kwadratem trójkąta prostokąt.przeciwprostokątna jest równa
sumie kwadratów pozostałych dwóch stron.,
pewnie … ?
zobaczmy, czy naprawdę działa na przykładzie.

dlaczego jest to przydatne?
jeśli znamy długość dwóch boków trójkąta prostokątnego, możemy znaleźć Długość trzeciego boku. (Ale pamiętaj, że działa tylko na Trójkąty pod kątem prostym!)
jak go używać?,
zapisz to jako równanie:
 |
a2 + b2 = c2 |
następnie używamy algebry, aby znaleźć brakujące wartości, jak w tych przykładach:
Możesz również przeczytać o kwadratach i korzeniach kwadratowych, aby dowiedzieć się, dlaczego √169 = 13
to działa odwrotnie również: gdy trzy boki trójkąta tworzą a2 + b2 = c2, wtedy trójkąt jest pod kątem prostym.,
i sam możesz udowodnić twierdzenie !
Pobierz papierowy długopis i nożyczki, a następnie użyj poniższej animacji jako przewodnika:
- narysuj na papierze trójkąt prostokątny, pozostawiając dużo miejsca.,
- narysuj kwadrat wzdłuż przeciwprostokątnej (najdłuższej strony)
- narysuj kwadrat tego samego rozmiaru po drugiej stronie przeciwprostokątnej
- narysuj linie, jak pokazano na Animacji, w następujący sposób:

- Wytnij kształty
- ułóż je, aby udowodnić, że duży kwadrat ma ten sam obszar, co dwa kwadraty na przeciwprostokątnej.pozostałe boki
kolejny, niezwykle prosty dowód
oto jeden z najstarszych dowodów na to, że kwadrat po długiej stronie ma taką samą powierzchnię jak pozostałe kwadraty.,
oglądaj animację i zwracaj uwagę, gdy Trójkąty zaczną się przesuwać.
możesz obejrzeć animację kilka razy, aby zrozumieć, co się dzieje.
fioletowy trójkąt jest ważny.
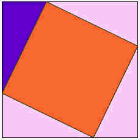 |
staje się | 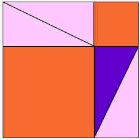 |

