wykładnik liczby mówi, ile razy użyć liczby w mnożeniu.
w 82 „2” mówi, aby użyć 8 dwa razy w mnożeniu,
więc 82 = 8 × 8 = 64
w słowach: 82 można nazwać „8 do potęgi 2” lub „8 do drugiej potęgi”, lub po prostu „8 do kwadratu”
Wykładniki są również nazywane potęgami lub indeksami.,p>jeszcze kilka przykładów:
przykład: 53 = 5 × 5 × 5 = 125
- w słowach: 53 można nazwać „5 do trzeciej potęgi”, „5 do potęgi 3” lub po prostu „5 do potęgi 3”
przykład: 24 = 2 × 2 × 2 × 2 = 16
- w słowach: 24 można nazwać „2 do czwartej potęgi” lub „2 do czwartej potęgi” lub po prostu „2 do czwartej potęgi”
Wykładniki ułatwiają pisanie i używanie wielu mnożeń
przykład: 96 jest łatwiejszy do zapisu i odczytu niż 9 × 9 × 9 × 9 × 9 × 9
możesz pomnożyć dowolną liczbę przez siebie tyle razy, ile chcesz, używając wykładników.,
spróbuj tutaj:
ogólnie
tak ogólnie:
| an mówi, aby pomnożyć a przez siebie, więc jest n tych a”S: |
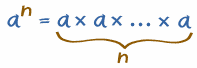 |
inny sposób zapisu
czasami ludzie używają symbolu ^ (powyżej 6 na klawiaturze), ponieważ jest łatwy do wpisania.
przykład: 2^4 jest taki sam jak 24
- 2^4 = 2 × 2 × 2 × 2 = 16
ujemne Wykładniki
ujemne?, Co może być przeciwieństwem mnożenia? Dzielenie!
więc dzielimy za każdym razem przez liczbę, która jest taka sama jak mnożenie przez 1number
przykład: 8-1 = 18 = 0.125
możemy kontynuować tak:
przykład: 5-3 = 15 × 15 × 15 = 0.008
ale często łatwiej jest to zrobić w ten sposób:
5-3 można również obliczyć tak:
15 × 5 × 5 = 153 = 1125 = 0.008
negatywny? Odwróć pozytyw!,
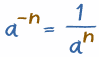 |
ten ostatni przykład pokazał łatwiejszy sposób obsługi ujemnych wykładników:
|
More Examples:
| Negative Exponent | Reciprocal of Positive Exponent |
Answer | ||
|---|---|---|---|---|
| 4-2 | = | 1 / 42 | = | 1/16 = 0.0625 |
| 10-3 | = | 1 / 103 | = | 1/1,000 = 0.001 |
| (-2)-3 | = | 1 / (-2)3 | = | 1/(-8) = -0.,125 |
co jeśli wykładnik wynosi 1, Czy 0?
| 1 | jeśli wykładnik wynosi 1, to po prostu masz sam numer (przykład 91 = 9) | |
| 0 | jeśli wykładnik wynosi 0, otrzymasz 1 (przykład 90 = 1) | |
to wszystko ma sens
Jeśli spojrzysz na tę tabelę, zobaczysz, że wykładniki dodatnie, zerowe lub ujemne są naprawdę częścią tego samego (dość prostego) wzoru:
