„I, w dowolnym Oceń, jestem przekonany, że nie rzuca kostką.,”
~ Albert Einstein
- Zmienne losowe
- Zmienne losowe dyskretne
- Zmienne losowe ciągłe
- Zmienne losowe mieszane
- funkcje rozkładu kumulacyjnego (CDF)
- funkcja gęstości prawdopodobieństwa (PDF)
- interaktywny przykład CDF/PDF
zmienne losowe:

powiedz, że masz wziąć monetę z kieszeni i wyrzucić ją w powietrze. Co mógłbyś powiedzieć o jego przyszłości?
czy wyląduje? Reszka?, Co więcej, jak długo pozostanie w powietrzu? Ile razy się odbije? Jak daleko od miejsca, w którym po raz pierwszy uderzy w ziemię, czy w końcu spocznie? Czy kiedykolwiek uderzy w ziemię? Przyszedłeś kiedyś odpocząć?
w przypadku niektórych takich pytań możemy i rozstrzygamy na długo przed obserwacjami.jesteśmy prawie pewni, że grawitacja wytrzyma i moneta wyląduje. Ale dla innych nie mamy innego wyboru, jak tylko osądzić i mówić bardziej ogólnikowo, jeśli chcemy w ogóle powiedzieć coś pożytecznego o przyszłości.,
jako naukowcy, oczywiście naszym zadaniem jest powiedzieć coś użytecznego (a przynajmniej autorytatywnego…), podczas gdy metaforyczne monety ważnego układu fizycznego wciąż wisiały w powietrzu. Orzeł czy reszka może być nawet kwestią życia lub śmierci. Naszymi monetami mogą być na przykład różne możliwe natężenia przepływu chłodziwa lub masy uranu w elektrowni jądrowej. Bardzo zależy nam na tym, aby wiedzieć, jakie są nasze szanse na to, że zamiast stopienia dostaniemy turbiny wirujące.,
dla ścisłego deterministy wszystkie takie zakłady zostały rozliczone na długo przed wybiciem jakiejkolwiek monety, metaforycznej lub nie, po prostu jeszcze jej nie znamy. Gdybyśmy tylko znali siły stosowane w rzucie monetą, jego dokładny rozkład masy, różne ruchy powietrza w pomieszczeniu… Gdybyśmy wiedzieli to wszystko, wiedziałybyśmy, że dany rzut monetą ma 100% szans na lądowanie w taki sposób, w jaki wyląduje, i zerową szansę na jakikolwiek inny wynik.
ale my, oczywiście, często brakuje nawet wymienialnej części takiej wiedzy o świecie., Co więcej, wydaje się, że na wyjątkowo małych skalach ścisli determiniści są absolutnie w błędzie; nie ma sposobu, aby przewidzieć, kiedy na przykład atom uranu się rozdzieli, a jeśli takie zdarzenie wpłynie na większy świat, to zdarzenie makro jest naprawdę nieprzewidywalne. Niektóre wyniki naprawdę są w powietrzu, niespokojne, dopóki nie staną się częścią przeszłości.
aby poradzić sobie z tą rzeczywistością i móc w jakiś użyteczny sposób opisać przyszłe Stany systemu, używamy zmiennych losowych., Zmienna losowa jest po prostu funkcją, która odnosi każdy możliwy fizyczny wynik systemu do jakiejś unikalnej, rzeczywistej liczby. Jako takie istnieją trzy rodzaje zmiennych losowych: Dyskretna, ciągła i mieszana. W kolejnych sekcjach kategorie te zostaną krótko omówione i podane przykłady.
dyskretne Zmienne losowe:
rozważmy ponownie rzut monetą. Możemy mieć orzeł lub reszka jako możliwe rezultaty. Jeśli zdefiniujemy zmienną x jako liczbę głów w jednym rzucie, to x może być 1 lub 0, nic więcej., Taka funkcja, x, byłaby przykładem dyskretnej zmiennej losowej. Takie zmienne losowe mogą przyjmować tylko wartości dyskretne. Innymi przykładami mogą być możliwe wyniki testu ciążowego lub liczba uczniów w klasie.
Zmienne losowe ciągłe:
Wracając do rzutu monetą, co by było, gdybyśmy chcieli opisać odległość między miejscem, w którym nasza moneta spoczywała, a miejscem, w którym po raz pierwszy uderzyła o ziemię. Ta odległość, x, byłaby ciągłą zmienną losową, ponieważ mogłaby przyjąć nieskończoną liczbę wartości w zakresie ciągłym liczb rzeczywistych., Moneta mogła podróżować 1 cm, lub 1,1 cm, lub 1,11 cm, lub dalej i dalej. Inne przykłady ciągłych zmiennych losowych to masa gwiazd w naszej galaktyce, pH wód oceanicznych lub czas przebywania jakiegoś analitu w chromatografie gazowym.
mieszane Zmienne losowe:
mieszane zmienne losowe mają zarówno elementy dyskretne, jak i ciągłe. Takie zmienne losowe są rzadko spotykane. W przypadku możliwego przykładu możesz jednak mierzyć wagę próbki i zdecydować, że każda waga mierzona jako wartość ujemna otrzyma wartość 0., W ten sposób zmienna losowa ma składową dyskretną Przy x = 0 i składową ciągłą, gdzie x > 0.
Cumulative Distribution Functions (CDF):
pojawia się oczywiście pytanie, jak najlepiej matematycznie opisać (i wizualnie wyświetlić) zmienne losowe. Do tych zadań używamy funkcji gęstości prawdopodobieństwa (PDF) i funkcji gęstości skumulowanej (CDF). Ponieważ CDFs są prostsze do zrozumienia zarówno dla dyskretnych, jak i ciągłych zmiennych losowych niż pliki PDF, najpierw wyjaśnimy CDFs.
rozważ rzucenie uczciwą 6-boczną kostką., Mamy 1 do 6 szans na uzyskanie dowolnej z możliwych wartości zmiennej losowej (1, 2, 3, 4, 5, lub 6). Jeśli wykreślimy te Możliwe wartości na osi x i wykreślimy prawdopodobieństwo zmierzenia każdej określonej wartości, x lub dowolnej wartości mniejszej niż x na osi y, będziemy mieć CDF zmiennej losowej.
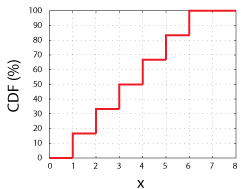
CDF za sprawiedliwą 6-boczną kostkę. Należy pamiętać, że każdy krok to wysokość 16,67%, czyli 1 na 6.
Ta funkcja, CDF (x), po prostu mówi nam o szansach zmierzenia dowolnej wartości do X włącznie., Jako takie, Wszystkie CDF muszą mieć następujące cechy:
- a CDF musi być równe 0, gdy x= -∞, a podejście 1 (lub 100%) jako X zbliża się +∞. Po prostu, ze wszystkich możliwych wyników, musi być wynik; szansa na rzucenie sześcioboczną kostką i uzyskanie wartości między – ∞ i ∞ wynosi 100%.
- nachylenie CDF musi być zawsze równe lub większe od zera. Na przykład, rozważmy szansę na rzucenie 6-boczną kostką (uczciwą lub nie) i uzyskanie wartości od 0 do 4., Ta szansa nie może być większa niż szansa na uzyskanie wartości między 0 a 5, ponieważ szanse na lądowanie 1, 2 lub 3 są, oczywiście, zawsze będą pewnym ułamkiem szans na zdobycie 1, 2, 3 lub 4.
dla przykładu ciągłej zmiennej losowej, poniższy aplet pokazuje rozkład normalnie CDF.,div>
| -5 | 5 |
| x | |
This important distribution is discussed elsewhere., Wystarczy zauważyć, że cechy CDF opisane powyżej i wyjaśnione dla dyskretnej zmiennej losowej utrzymują się również dla ciągłych zmiennych losowych.
aby uzyskać bardziej intuicyjne przykłady właściwości plików CDF, zobacz poniższy interaktywny przykład. Ponadto interaktywne wykresy wielu innych CDF ważnych dla dziedziny statystyki i używanych na tej stronie można znaleźć tutaj.
funkcje gęstości prawdopodobieństwa (PDF):
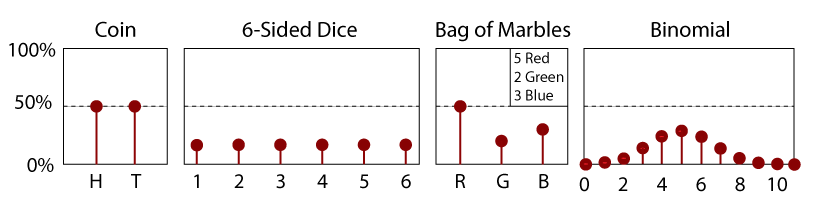
PDF for a Fair 6-Sidded Dice.
PDF jest po prostu pochodną CDF., Tak więc PDF jest również funkcją zmiennej losowej, x, a jego wielkość będzie pewnym wskaźnikiem względnego prawdopodobieństwa pomiaru określonej wartości. Ponieważ jest to nachylenie CDF, plik PDF musi zawsze być pozytywny; nie ma negatywnych szans na jakiekolwiek zdarzenie. Ponadto, z definicji, pole pod krzywą PDF (x) między -∞ I x jest równe jego CDF (x). Jako takie, pole pomiędzy dwoma wartościami x1 i x2 daje prawdopodobieństwo zmierzenia wartości w tym zakresie.
poniższy aplet pokazuje przykład pliku PDF dla normalnie rozłożonej zmiennej losowej, x.,
Normal PDF
|
x:
| mean:
| stdev:
| f(x):
|
|
Notice, when the mean and standard deviations are equal, how the PDF correlates with the normal CDF in the section above., rozważ również różnicę między ciągłym a dyskretnym PDF. Podczas gdy dyskretny plik PDF (taki jak pokazany powyżej w przypadku kości) daje szanse na uzyskanie określonego wyniku, Prawdopodobieństwo w przypadku ciągłych plików PDF jest kwestią zakresu, a nie dyskretnych punktów. Na przykład, istnieje 1 do 6 (16,6%) szansa na wyrzucenie 3 na kostkę, jak widać w pliku PDF. Ale jakie są dziwne mierzenie dokładnie zera ze zmienną losową o normalnym formacie PDF i średniej zera, jak pokazano powyżej? Chociaż jest to wartość, w której PDF jest największy, szansa na pomiar dokładnie 0.00000..,. jest, być może intuicyjnie, zerem. Prawdopodobieństwo zmierzenia dowolnej liczby losowej z nieskończoną dokładnością jest w rzeczywistości zerowe. w ciągłym pliku PDF możesz zamiast tego zapytać, jakie są kursy, aby zmierzyć między dwiema wartościami, aby uzyskać prawdopodobieństwo większe niż zero. Aby znaleźć to prawdopodobieństwo, po prostu używamy CDF naszej zmiennej losowej., Ponieważ CDF mówi nam nieparzyste pomiaru wartości lub cokolwiek niższego od tej wartości, aby znaleźć Prawdopodobieństwo pomiaru między dwiema wartościami, x1 i x2 (gdzie X1 > x2), po prostu musimy wziąć wartość CDF na X1 i odjąć od niej wartość CDF na x2. Na przykład, używając normalnego CDF w aplecie powyżej(z μ=0 i σ=1), jeśli chcemy znać szanse mierzenia między 0,01 a 0,02 znajdujemy CDF(x=0,1)=53,9828% i CDF (x=0,2)=57,9260%. Wtedy różnica, CDF(0,2)-CDF (0,1), daje nam szanse około 3,9% pomiaru x między 0,1 a 0,2., aby uzyskać bardziej intuicyjne, wizualne przykłady właściwości plików PDF, zobacz poniższy interaktywny przykład. Również interaktywne wykresy wielu ważnych plików PDF używanych na tej stronie można zobaczyć tutaj. |
|||||||||||||||||