8.1 historyczny przykład
w swojej książce dwie nowe nauki Galileo Galilea (1564-1642) podaje kilka argumentów mających na celu wykazanie, że nie może istnieć coś takiego jak rzeczywiste nieskończoności lub rzeczywiste nieskończoności. Jeden z jego argumentów można zrekonstruować w następujący sposób. Galileusz proponuje przyjąć jako założenie, że istnieje rzeczywista nieskończoność liczb naturalnych (liczby naturalne są dodatnimi liczbami całkowitymi od 1):
{1, 2, 3, 4, 5, 6, 7, ….,}
proponuje również przyjąć jako założenie, że istnieje rzeczywista nieskończoność kwadratów liczb naturalnych.
{1, 4, 9, 16, 25, 36, 49, ….}
teraz, z powodów Galileusza, zauważ, że te dwie grupy (dziś nazwalibyśmy je „zbiorami”) mają tę samą wielkość. Widzimy to, ponieważ widzimy, że istnieje korespondencja jeden do jednego między tymi dwoma grupami.,
| {1, | 2, | 3, | 4, | 5, | 6, | 7, ….,div> | |
{1, | 4, | 9, | 16, | 25, | 36, | 49,…} |
Jeśli możemy powiązać każdą liczbę naturalną z jedną i tylko jedną liczbą kwadratową, a jeśli możemy powiązać każdą liczbę kwadratową z jedną i tylko jedną liczbą naturalną, to zbiory te muszą być tej samej wielkości.,
ale poczekaj chwilę-mówi Galileusz. Istnieje oczywiście o wiele więcej liczb naturalnych niż liczb kwadratowych. Oznacza to, że każda liczba kwadratowa znajduje się na liście liczb naturalnych, ale wiele liczb naturalnych nie znajduje się na liście liczb kwadratowych. Poniższe liczby znajdują się na liście liczb naturalnych, ale nie na liście liczb kwadratowych.
{2, 3, 5, 6, 7, 8, 10, ….,}
Tak więc, jeśli w grupie liczb naturalnych jest wiele liczb, które nie należą do grupy liczb kwadratowych i jeśli w grupie liczb kwadratowych nie ma liczb naturalnych, to liczby naturalne są większe od liczb kwadratowych. A jeśli grupa liczb naturalnych jest większa od grupy liczb kwadratowych, to liczby naturalne i liczby kwadratowe nie są tej samej wielkości.,
doszliśmy do dwóch wniosków: zbiór liczb naturalnych i zbiór liczb kwadratowych są tej samej wielkości; a zbiór liczb naturalnych i zbiór liczb kwadratowych nie są tej samej wielkości. To sprzeczne.
Galileusz twierdzi, że powodem, dla którego osiągnęliśmy sprzeczność, jest założenie, że istnieją rzeczywiste nieskończoności. Stwierdza zatem, że nie ma rzeczywistych nieskończoności.
8.2 dowody pośrednie
nasza logika nie jest jeszcze wystarczająco silna, aby udowodnić pewne ważne argumenty. Rozważ następujący argument jako przykład.,
(p→(QvR))
Q
R
p
ten argument wygląda na poprawny. Z pierwszego założenia wiemy: gdyby P było prawdą, to tak (Q v R) byłoby prawdą. Ale wtedy albo Q albo R albo oba byłyby prawdziwe. A z drugiego i trzeciego przesłanki wiemy: Q jest fałszywe, A R jest fałszywe. Więc nie może być tak, że (Q v R) jest prawdą, a więc nie może być tak, że p jest prawdą.
możemy sprawdzić argument używając tabeli prawdy. Nasz stół będzie złożony, ponieważ jedno z naszych założeń jest złożone.,
In any kind of situation in which all the premises are true, the conclusion is true., Oznacza to, że wszystkie przesłanki są prawdziwe tylko w ostatnim rzędzie. Dla tego wiersza wniosek jest również prawdziwy. Więc jest to ważny argument.
ale poświęć chwilę i spróbuj udowodnić ten argument. Zaczynamy od

i teraz jesteśmy zatrzymani. Nie możemy stosować żadnych naszych zasad. Oto ważny argument, który nie sprawił, że nasz system rozumowania był wystarczająco silny, aby go udowodnić.
istnieje kilka sposobów na naprawienie tego problemu i uczynienie naszego systemu rozumowania wystarczająco silnym., Jednym z najstarszych rozwiązań jest wprowadzenie nowej metody dowodu, tradycyjnie zwanej „reductio ad absurdum”, co oznacza redukcję do absurdu. Metoda ta jest również często nazywana „dowodem pośrednim” lub „pochodną pośrednią”.
chodzi o to, że zakładamy zaprzeczenie naszej konkluzji, a następnie pokazujemy, że sprzeczność skutkuje. Sprzeczność jest pokazywana, gdy udowodnimy jakieś zdanie Ψ, a jego negację Ψ. To może być dowolne zdanie. Chodzi o to, że biorąc pod uwagę zasadę dwuwartościowości, musieliśmy udowodnić coś nieprawdziwego. Bo jeśli Ψ jest prawdziwe, to Ψ jest fałszywe; a jeśli Ψ jest prawdziwe, to Ψ jest fałszywe., Nie musimy wiedzieć, co jest fałszywe (Ψ lub Ψ); wystarczy wiedzieć, że jeden z nich musi być.
pamiętaj, że zbudowaliśmy nasz system logiczny tak, że nie może on wytwarzać fałszu z prawdziwych stwierdzeń. Źródłem fałszu, który produkujemy w wyprowadzeniu pośrednim, musi być więc jakiś fałsz, który dodaliśmy do naszego argumentu. A to, co dodaliśmy do naszego argumentu, to zaprzeczenie konkluzji. Tak więc wniosek musi być prawdziwy.,
kształt argumentu jest następujący:

tradycyjnie, założenie dla wyprowadzenia pośredniego jest również powszechnie nazywane „założeniem dla reductio”.
jako konkretny przykład możemy udowodnić naszą kłopotliwą sprawę.

przyjęliśmy odmowę naszej konkluzji na linii 4. Wniosek, który uważaliśmy za poprawny, to P, A zaprzeczeniem tego jest P. w linii 7 udowodniliśmy R., Technicznie rzecz biorąc, skończyliśmy na tym etapie, ale chcielibyśmy być mili dla każdego, kto próbuje zrozumieć nasz dowód, więc powtarzamy linię 3 tak, że zdania R i R są obok siebie i bardzo łatwo jest zobaczyć, że coś poszło nie tak. Oznacza to, że jeśli udowodniliśmy zarówno R, jak i R, to udowodniliśmy coś fałszywego.
nasze rozumowanie teraz wygląda tak. Co poszło nie tak? Linia 8 to poprawne użycie powtórzeń; linia 7 pochodzi z poprawnego użycia Modus tollendo ponens; linia 6 z poprawnego użycia Modus ponens; linia 5 z poprawnego użycia podwójnej negacji., Nie popełniliśmy więc błędu w naszym rozumowaniu. Użyliśmy linii 1, 2 i 3, ale te założenia zgodziliśmy się założyć, że są poprawne. Zostaje linia 4. To musi być źródło mojej sprzeczności. To musi być fałszywe. Jeśli linia 4 jest false, to p jest true.
niektórzy uważają dowody pośrednie za mniej mocne niż dowody bezpośrednie. Istnieje wiele i złożonych przyczyn tego stanu rzeczy. Ale, dla naszej logiki propozycji, żaden z tych powodów nie ma zastosowania. Możliwe jest bowiem udowodnienie, że nasza logika wnioskowania jest spójna., Oznacza to, że można udowodnić, że nasza logika wnioskowania nie może udowodnić fałszu, chyba że najpierw wprowadzi się fałsz do systemu. (Generalnie nie jest możliwe udowodnienie, że silniejsze i bardziej zaawansowane systemy logiczne lub matematyczne są spójne, z wewnątrz tych systemów; na przykład, nie można udowodnić w arytmetyce, że arytmetyka jest spójna.) Biorąc pod uwagę, że możemy być pewni spójności logiki wnioskowania, możemy być pewni, że w naszej logice wnioskowania dowód pośredni jest dobrą formą rozumowania., Wiemy, że jeśli udowodnimy fałsz, musimy umieścić fałsz w; i jeśli jesteśmy pewni wszystkich innych założeń (to jest przesłanek) naszego dowodu, z wyjątkiem założenia dla pośredniego wyprowadzenia, to możemy być pewni, że to założenie dla pośredniego wyprowadzenia musi być źródłem fałszu.
wymagana jest tutaj uwaga dotycząca terminologii. Słowo „sprzeczność” jest używane dwuznacznie w większości dyskusji logicznych. Może to oznaczać sytuację, jak widzimy powyżej, gdzie dwa zdania są twierdzone, a te zdania nie mogą być prawdziwe., Albo może oznaczać jedno zdanie, które nie może być prawdziwe. Przykładem takiego zdania jest (P^P)., Tabela prawdy dla tego zdania to:
| P | (p ^ p) | |
|---|---|---|
| P | (p ^ p) | T | F | f |
| F | T | f |
tak więc tego rodzaju zdanie nigdy nie może być prawdziwe, niezależnie od znaczenia p.,
aby uniknąć dwuznaczności, w tym tekście zawsze będziemy nazywać pojedyncze zdanie, które nie może być prawdziwe „zdaniem sprzecznym”. Tak więc (P^P) jest zdaniem sprzecznym. Sytuacje, w których dwa zdania są twierdzone, że oba nie mogą być prawdziwe, nazywa się”sprzecznością”.
8.3 nasz przykład i inne przykłady
możemy teraz zrekonstruować wersję argumentu Galileusza. Użyjemy następującego klucza.
p: istnieją nieskończoności rzeczywiste (w tym liczby naturalne i liczby kwadratowe).,
p: istnieje zbieżność między liczbami naturalnymi a liczbami kwadratowymi.
R: rozmiar zbioru liczb naturalnych i rozmiar zbioru liczb kwadratowych są takie same.
s: wszystkie liczby kwadratowe są liczbami naturalnymi.
T: niektóre liczby naturalne nie są liczbami kwadratowymi.
U: jest więcej liczb naturalnych niż liczb kwadratowych.,
za pomocą tego klucza argument zostanie przetłumaczony:
(p→Q)
(Q→R)
(p→(S^T))
((S^T)→U)
(U→R)
p
i możemy udowodnić, że jest to prawidłowy argument za pomocą pośredniej pochodnej:

on line 6, założyliśmy, że p ponieważ Galileo wierzył, że p i miał na celu udowodnić, że P. to znaczy, on wierzył, że nie ma rzeczywistych nieskończoności, i tak założył, że było fałszywe wierzyć, że nie jest to przypadek, że nie ma rzeczywistych nieskończoności. To kłamstwo doprowadzi do innych kłamstw, ujawniając się.,
dla zainteresowanych: Galileusz doszedł do wniosku, że nie ma rzeczywistych nieskończoności, ale istnieją potencjalne nieskończoności. Tak więc, rozumował, nie jest tak ,że wszystkie liczby naturalne istnieją (w pewnym sensie „istnieją”), ale prawdą jest, że można liczyć liczby naturalne na zawsze. Wielu filozofów przed i po Galileusza utrzymał ten pogląd; jest podobny do poglądu posiadanego przez Arystotelesa, który był ważnym logik i filozof pisanie prawie dwa tysiące lat przed Galileuszem.,
zauważ, że w takim argumencie można wnioskować, że nie założenie o wyprowadzeniu pośrednim, ale raczej jeden z przesłanek był źródłem sprzeczności. Dziś większość matematyków uważa to za argument Galileusza. Logik i matematyk Georg Cantor (1845-1918), wynalazca teorii mnogości, twierdził, że zbiory nieskończone mogą mieć odpowiednie podzbiory tej samej wielkości., Oznacza to, że Cantor zaprzeczył przesłance 4 powyżej: mimo że wszystkie liczby kwadratowe są liczbami naturalnymi, a nie wszystkie liczby naturalne są liczbami kwadratowymi, nie jest tak, że te dwa zbiory są różnej wielkości. Cantor przyjął jednak założenie 2 powyżej i dlatego uważał, że wielkość zbioru liczb naturalnych i wielkość zbioru liczb kwadratowych jest taka sama. Dziś, korzystając z rozumowania Cantora, matematycy i logicy badają nieskończoność i rozwinęli dużą wiedzę o naturze nieskończoności. Jeśli to Cię interesuje, patrz punkt 17.5.,
rozważmy inny przykład do zilustrowania wyprowadzenia pośredniego. Bardzo przydatny zestaw twierdzeń nazywa się dziś „twierdzeniami De Morgana”, po logikan Augustus De Morgan (1806-1871). Nie możemy podać ich w pełni do rozdziału 9, ale możemy podać ich odpowiednik w języku angielskim: DeMorgan zauważył, że (PvQ) i (P^Q) są równoważne, a także że (P^Q) i (PvQ) są równoważne. Biorąc to pod uwagę, powinno to być twierdzenie naszego języka, że ((PvQ)→(P^Q)). Udowodnijmy to.
Cała formuła jest warunkowa, więc użyjemy wyprowadzenia warunkowego., Nasz dowód musi się więc rozpocząć:
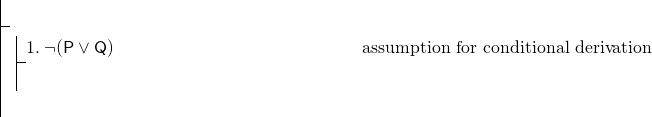
aby zakończyć wyprowadzenie warunkowe, musimy udowodnić (P^Q). Jest to koniunkcja, a naszą regułą pokazywania koniunkcji jest adjunction. Ponieważ użycie tej reguły może być naszym najlepszym sposobem na pokazanie (P^Q), możemy dążyć do pokazania P, a następnie pokazać Q, A następnie wykonać adjunction. Ale oczywiście mamy bardzo mało do pracy-tylko linia 1, która jest negacją. W takim przypadku zwykle rozsądnie jest próbować dowodu pośredniego. Zacznij od pośredniego dowodu P.,

musimy teraz znaleźć sprzeczność—każdą sprzeczność. Ale jest już jeden oczywisty. Linia 1 mówi, że ani P, ani Q nie są prawdziwe. Ale linia 3 mówi, że P jest prawdą. Musimy uczynić tę sprzeczność wyraźną, znajdując formułę i jej zaprzeczenie. Możemy to zrobić za pomocą dodawania.

aby ukończyć dowód, użyjemy tej strategii ponownie.

udowodnimy twierdzenia De Morgana jako problemy w rozdziale 9.,
oto ogólna zasada wykonywania dowodów: podczas udowodnienia warunkowego zawsze wykonuj derywację warunkową; w przeciwnym razie spróbuj derywacji bezpośredniej; jeśli to się nie powiedzie, spróbuj derywacji pośredniej.
8.4 problemy
- wypełnij poniższe dowody. Każdy z nich będzie wymagał wyprowadzenia pośredniego. Ostatnie dwa są trudne.
- udowodnij następujące twierdzenia.
- (p^P).
- ((P→P)^(p→P)).
- (P→(p^Q)).
- ((P^Q)→(P→Q)).
- w normalnym potocznym języku angielskim napisz swój własny ważny argument z co najmniej dwoma przesłankami., Twój argument powinien być tylko akapitem (a nie uporządkowaną listą zdań lub czymkolwiek innym, co wygląda jak logika formalna). Przetłumaczyć go na logikę wnioskowania i udowodnić, że jest ważny za pomocą pochodnej pośredniej.
to tłumaczenie tytułu książki Galileusza stało się najczęstszym, choć bardziej dosłownym byłoby Matematyczne dyskursy i demonstracje. Tłumaczenia książki to m.in. Drake (1974).