Content-Probability density functions

Content

Probability density functions

probability density function (pdf) \(F(x)\) of a continuous random variable \(X\) definieras som derivatet av CDF \(f(x)\):

\

det är ibland användbart att överväga CDF \(F(x)\) när det gäller pdf \(f(x PDF\(F(X)\) har två viktiga egenskaper:

1. \(f(x)\ geq 0\), för alla \(x\)
2. \(\displaystyle \int_ {- \infty}^{\infty} f(x)\; dx = 1\).,

en oändlig mängd olika former är möjliga för en pdf, eftersom de enda kraven är de två egenskaperna ovan. Pdf kan ha en eller flera toppar, eller inga toppar alls; det kan ha diskontinuiteter, bestå av kombinationer av funktioner, och så vidare. figur 5 visar en pdf med en enda topp och lite mild skevhet. Som är fallet för en typisk pdf, värdet av funktionen närmar sig noll som \(x \ till \ infty\) och \(x \till -\infty\).

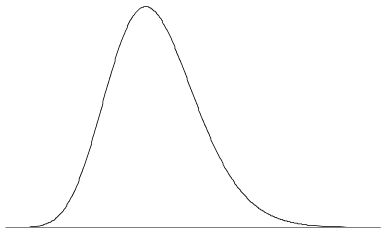
Figur 5: en pdf kan se ut så här.,

vi utforskar nu hur sannolikheter för den kontinuerliga slumpmässiga variabeln \(X\) relaterar till dess pdf. Det viktiga resultatet här är att

\_a^b.\]

detta resultat följer av det faktum att båda sidor är lika med \(f(b) – f(a)\).

anmärkningar.

• för en kontinuerlig slumpmässig variabel måste vi överväga sannolikheten att den ligger i ett intervall. Betydelsen av detta resultat är att det berättar för oss att för att hitta sannolikheten måste vi hitta området under pdf-filen på det givna intervallet.
• den totala ytan under pdf är lika med 1., Så det här resultatet berättar för oss att för att approximera sannolikheten för att den slumpmässiga variabeln ligger i ett visst intervall måste vi bara gissa fraktionen av området under pdf mellan intervallets ändar.
• detta resultat ger ett annat perspektiv på varför PDF-filer inte kan vara negativa, eftersom om de var, en negativ Sannolikhet kunde erhållas, vilket är omöjligt.
• pdf-filen är analog med, men skiljer sig från, sannolikhetsfunktionen (PF) för en diskret slumpvariabel. En pf ger en sannolikhet, så det kan inte vara större än en., En pdf \(F(x)\) kan dock ge ett värde större än ett för vissa värden av \(x\), eftersom det inte är värdet av \(F(x)\) Men området under kurvan som representerar Sannolikhet. Å andra sidan återspeglar kurvens höjd den relativa sannolikheten. Om \(f(b) = 2f(A)\) är en observation nära \(B\) ungefär dubbelt så sannolikt som en observation nära \(a\).,

Nästa sida – innehåll – medelvärde och varians för en kontinuerlig slumpvariabel