8.1 ett historiskt exempel
i sin bok ger de två nya vetenskaperna Galileo Galilea (1564-1642) flera argument avsedda att visa att det inte kan finnas något sådant som faktiska infiniteter eller faktiska infinitesimaler. Ett av hans argument kan rekonstrueras på följande sätt. Galileo föreslår att vi utgår från att det finns en faktisk oändlighet av naturliga tal (de naturliga siffrorna är de positiva heltal från 1 till):
{1, 2, 3, 4, 5, 6, 7, ….,}
han föreslår också att vi utgår från att det finns en faktisk oändlighet av kvadraterna för de naturliga siffrorna.
{1, 4, 9, 16, 25, 36, 49, ….}
Nu, Galileo skäl, notera att dessa två grupper (idag skulle vi kalla dem ”Set”) har samma storlek. Vi kan se detta eftersom vi kan se att det finns en en-till-en-korrespondens mellan de två grupperna.,
| {1, | 2, | 3, | 4, | 5, | 6, | 7, ….,div> | |
| {1, | 4, | 9, | 16, | 25, | 36, | 49, …} |
om vi kan associera varje naturligt nummer med ett och bara ett kvadratiskt nummer, och om vi kan associera varje kvadratiskt nummer med ett och bara ett naturligt nummer, måste dessa uppsättningar vara samma storlek.,
men vänta en stund, säger Galileo. Det finns uppenbarligen mycket många fler naturliga tal än det finns fyrkantiga tal. Det vill säga varje kvadratnummer finns i listan över naturliga tal, men många av de naturliga siffrorna finns inte i listan över kvadratnummer. Följande nummer finns alla i listan över naturliga nummer men inte i listan över kvadratiska nummer.
{2, 3, 5, 6, 7, 8, 10, ….,}
så, Galileo skäl, om det finns många siffror i gruppen av naturliga tal som inte är i gruppen av kvadratiska tal, och om det inte finns några siffror i gruppen av kvadratiska tal som inte är i naturals nummer, då de naturliga siffrorna är större än kvadratiska tal. Och om gruppen av de naturliga siffrorna är större än gruppen av kvadratnumren, är de naturliga siffrorna och kvadratnumren inte samma storlek.,
Vi har nått två slutsatser: uppsättningen av de naturliga siffrorna och uppsättningen av kvadratnumren är samma storlek; och uppsättningen av de naturliga siffrorna och uppsättningen av kvadratnumren är inte samma storlek. Det är motsägelsefullt.
Galileo hävdar att anledningen till att vi nådde en motsägelse är att vi antog att det finns faktiska infiniteter. Han drar därför slutsatsen att det inte finns några faktiska infiniteter.
8.2 indirekta bevis
vår logik är ännu inte tillräckligt stark för att bevisa några giltiga argument. Tänk på följande argument som ett exempel.,
(p→(QvR))
Q
r
p
detta argument ser giltigt ut. Vid den första förutsättningen vet vi: om P var sant, så skulle (Q v R) vara sant. Men då skulle antingen Q eller R eller båda vara sanna. Och vid andra och tredje lokalerna vet vi: Q är falskt och R är falskt. Så det kan inte vara så (Q V R) är sant, och så kan det inte vara så att P är sant.
Vi kan kontrollera argumentet med hjälp av en sanningstabell. Vårt bord kommer att vara komplicerat eftersom en av våra premisser är komplex.,
In any kind of situation in which all the premises are true, the conclusion is true., Det vill säga: lokalerna är alla sanna endast i sista raden. För den raden är slutsatsen också sann. Så det här är ett giltigt argument.
men ta en minut och försök att bevisa detta argument. Vi börjar med

och nu stoppas vi. Vi kan inte tillämpa någon av våra regler. Här är ett giltigt argument att vi inte har gjort vårt resonemangssystem tillräckligt starkt för att bevisa.
det finns flera sätt att åtgärda detta problem och att göra vårt resonemang system tillräckligt stark., En av de äldsta lösningarna är att införa en ny bevismetod, traditionellt kallad ”reductio ad absurdum”, vilket innebär en minskning till absurditet. Denna metod kallas också ofta ett ”indirekt bevis”eller” indirekt härledning”.
tanken är att vi antar att vi förnekar vår slutsats och sedan visar att en motsägelse resulterar. En motsägelse visas när vi bevisar en mening, och dess negation. Detta kan vara vilken mening som helst. Poängen är att vi, med tanke på principen om bivalens, måste ha bevisat något falskt. För om det är sant är det falskt, och om det är sant är det falskt., Vi behöver inte veta vilket som är falskt (eller falskt); det räcker att veta att en av dem måste vara.
Kom ihåg att vi har byggt vårt logiska system så att det inte kan producera en lögn från sanna uttalanden. Källan till den lögn som vi producerar i den indirekta härledningen måste därför vara en del lögn som vi lade till i vårt argument. Och vad vi lade till i vårt argument är förnekandet av slutsatsen. Således måste slutsatsen vara sann.,
formen på argumentet är så här:

traditionellt har antagandet för indirekt härledning också kallats ”antagandet för reductio”.
som ett konkret exempel kan vi bevisa vårt förbryllande fall.

vi antog förnekandet av vår slutsats på rad 4. Slutsatsen vi trodde var korrekt var P, och förnekandet av detta är P. i linje 7 visade vi R., Tekniskt sett är vi klara vid den tidpunkten, men vi skulle vilja vara vänliga mot alla som försöker förstå vårt bevis, så vi upprepar rad 3 så att meningarna R och R är sida vid sida, och det är väldigt lätt att se att något har gått fel. Det vill säga, om vi har bevisat både R och R, så har vi bevisat något falskt.
vårt resonemang går nu så här. Vad gick fel? Linje 8 är en korrekt användning av upprepning, linje 7 kommer från en korrekt användning av modus tollendo ponens, linje 6 från en korrekt användning av modus ponens, linje 5 från en korrekt användning av dubbel negation., Så vi gjorde inte ett misstag i vårt resonemang. Vi använde linjer 1, 2 och 3, men det är lokaler som vi kom överens om att anta är korrekta. Detta lämnar linje 4. Det måste vara källan till min motsägelse. Det måste vara falskt. Om rad 4 är falsk, är P sant.
vissa människor anser indirekta bevis mindre starka än direkta bevis. Det finns många och komplexa skäl till detta. Men, för vår propositionslogik, gäller ingen av dessa skäl. Detta beror på att det är möjligt att bevisa att vår föreslagna logik är konsekvent., Det innebär att det är möjligt att bevisa att vår föreslagna logik inte kan bevisa en lögn om man inte först introducerar en lögn i systemet. (Det är i allmänhet inte möjligt att bevisa att mer kraftfulla och avancerade logiska eller matematiska system är konsekventa, inifrån dessa system; till exempel kan man inte bevisa i aritmetik att aritmetik är konsekvent.) Med tanke på att vi kan vara säkra på konsekvensen i den propositionella logiken kan vi vara säkra på att ett indirekt bevis i vår propositionslogik är en bra form av resonemang., Vi vet att om vi visar en lögn måste vi ha lagt en lögn i; och om vi är övertygade om alla andra antaganden (det vill säga lokalerna) av vårt bevis förutom antagandet om indirekt avledning, kan vi vara övertygade om att detta antagande för indirekt avledning måste vara källan till falskheten.
en anteckning om terminologi krävs här. Ordet ”motsägelse” används tvetydigt i de flesta logiska diskussioner. Det kan innebära en situation som vi ser ovan, där två meningar hävdas, och dessa meningar kan inte båda vara sanna., Eller det kan betyda en enda mening som inte kan vara sant. Ett exempel på en sådan mening är (P^P)., Sanningstabellen för denna mening är:
| p | p | (p ^ p) |
|---|---|---|
| t | f | f |
| f | t | f |
således kan denna typ av mening aldrig vara sant, oavsett betydelsen av P.,
för att undvika tvetydighet kommer vi i denna text alltid att kalla en enda mening som inte kan vara sann en ”motsägelsefull mening”. Således är (p^p) en motsägelsefull mening. Situationer där två meningar hävdas som inte kan båda vara sanna kommer att kallas en ”motsägelse”.
8.3 vårt exempel och andra exempel
Vi kan rekonstruera en version av Galileos argument nu. Vi kommer att använda följande nyckel.
p: det finns faktiska infiniteter (inklusive de naturliga siffrorna och kvadratnumren).,
Q: det finns en en-till-en korrespondens mellan de naturliga siffrorna och de fyrkantiga siffrorna.
R: storleken på uppsättningen av de naturliga siffrorna och storleken på uppsättningen av kvadratnumren är desamma.
s: alla fyrkantiga tal är naturliga tal.
T: några av de naturliga siffrorna är inte kvadratiska siffror.
U: det finns fler naturliga tal än kvadratiska tal.,
med denna nyckel kommer argumentet att översättas:
(p→Q)
(Q→r)
(p→(S^t))
((S^t)→u)
(U→R)
p
och vi kan bevisa att detta är ett giltigt argument genom att använda indirekt härledning:

på Linje 6 antog vi p eftersom Galileo trodde att p och syftade till att bevisa att P. det var, han trodde att det inte finns några faktiska Infiniteter, och så antog att det var felaktigt att tro att det inte är fallet att det inte finns några faktiska infiniteter. Denna lögn kommer att leda till andra lögner och utsätta sig själv.,
För dem som är intresserade: Galileo slutsatsen att det inte finns några faktiska infiniteter men det finns potentiella infiniteter. Således motiverade han, det är inte så att alla naturliga tal finns (i någon mening av ”existerar”), men det är sant att du kan räkna naturliga tal för alltid. Många filosofer före och efter Galileo höll denna uppfattning; det liknar en uppfattning som innehas av Aristoteles, som var en viktig logiker och filosof skriver nästan två tusen år före Galileo.,
Observera att i ett argument som detta kan du motivera att inte antagandet om indirekt härledning, utan snarare en av lokalerna var källan till motsägelsen. Idag tror de flesta matematiker detta om Galileos argument. En logiker och matematiker som heter Georg Cantor (1845-1918), uppfinnaren av set theory, hävdade att oändliga uppsättningar kan ha korrekta delmängder av samma storlek., Det vill säga, Cantor förnekade premiss 4 ovan: även om alla fyrkantiga tal är naturliga tal, och inte alla naturliga tal är kvadratiska tal, är det inte så att dessa två uppsättningar är av olika storlek. Cantor accepterade dock premiss 2 ovan, och därför trodde att storleken på uppsättningen av naturliga tal och storleken på uppsättningen av kvadratiska tal är densamma. Idag, med hjälp av Cantor resonemang, matematiker och logiker studera oändlighet, och har utvecklat en stor mängd kunskap om vilken typ av oändlighet. Om detta intresserar dig, se avsnitt 17.5.,
låt oss överväga ett annat exempel för att illustrera indirekt härledning. En mycket användbar uppsättning teoremer kallas idag ”De Morgans teoremer”, efter logikern Augustus De Morgan (1806-1871). Vi kan inte ange dessa helt förrän Kapitel 9, men vi kan ange deras motsvarighet på engelska: DeMorgan observerade att (PvQ) och (P^Q) är likvärdiga, och även att (P^Q) och (PvQ) är likvärdiga. Med tanke på detta bör det vara en sats på vårt språk som ((PvQ)→(P^Q)). Vi bevisar det här.
hela formeln är en villkorlig, så vi kommer att använda en villkorlig härledning., Vårt bevis måste således börja:
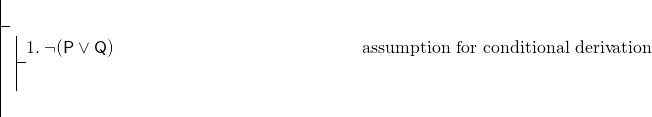
för att slutföra den villkorliga härledningen måste vi bevisa (P^Q). Detta är en kombination, och vår regel för att visa konjunktioner är adjunktion. Eftersom användningen av denna regel kan vara vårt bästa sätt att visa (P^Q) kan vi sträva efter att visa P och sedan visa Q och sedan utföra adjunktion. Men, vi har uppenbarligen mycket lite att arbeta med—bara linje 1, vilket är en negation. I ett sådant fall är det vanligtvis klokt att försöka ett indirekt bevis. Börja med ett indirekt bevis på P.,

Vi måste nu hitta en motsägelse—någon motsägelse. Men det finns redan en uppenbar. Linje 1 säger att varken P eller Q är sant. Men linje 3 säger att P är sant. Vi måste göra denna motsägelse tydlig genom att hitta en formel och dess förnekelse. Vi kan göra detta med tillägg.

för att slutföra beviset kommer vi att använda denna strategi igen.

Vi kommer att bevisa De Morgans teorem som problem för kapitel 9.,
här är en allmän tumregel för att göra bevis: när du visar en villkorlig, gör alltid villkorlig härledning; annars, försök direkt härledning; om det misslyckas, försök indirekt härledning.
8.4 problem
- fyll i följande bevis. Varje kommer att kräva en indirekt härledning. De två sista är utmanande.
- bevisa följande är satser.
- (p^p).
- ((p→p)^(p→p)).
- (p→(p^Q)).
- ((p^Q)→(p→Q)).
- på normal vardaglig engelska, skriv ditt eget giltiga argument med minst två lokaler., Ditt argument bör bara vara ett stycke (inte en ordnad lista över meningar eller något annat som ser ut som formell logik). Översätt det till propositionell logik och bevisa att det är giltigt med hjälp av en indirekt härledning.
denna översättning av titeln på Galileos bok har blivit den vanligaste, även om en mer bokstavlig skulle ha varit matematiska diskurser och demonstrationer. Översättningar av boken inkluderar Drake (1974).